第六章 图论与网络分析 （重点，熟练掌握三算法） 树图和图的最小部分树 最短路问题 网络的最大流

• 图的最小部分树

  • 注意

    • 1. 一个图的最小部分树不唯一

    • 2. 每个最小部分树中所有边权的总和一定都是相同的，即都达到了最小。

  • 避圈法

    • 法一

      • 1.从图中任选一点 vi ，让 vi ∈V ，图中其余点均包含在V（-）中；

      • 2. 从 V 与 的连线中找出最小边，这条边一定包含在最小部分树中，不妨设这条边为[vi , vj]将其加粗，标记为最小部分树中的边。

      • 3. 令 V∪vj→V，V（-） - vj → V（-） ；

      • 4. 重复2、3两步，一直到图中所有点均包含在 V 中。

      • 简洁版

        • 添加相邻最小边

    • 法二

      • 1.在所有各边中找到边权最小的一条，将其作为最小部分树中的第一边；

      • 2.在剩余的边中，找到边权最小的边，查看其是否与前面的边形成圈，如果没有，则在最小部分树中添加该边，如果形成了圈，则不再考虑该边；

      • 3.重复进行第二步，直到找到第 n-1 条边为止。（因为有 n 个顶点的树中一定有 n-1 条边）

      • 简洁版

        • 添加最小边

  • 破圈法

    • 1. 从图 N 中任取一回路，去掉这个回路中边权最大的边，得到原图的一个子图 N1。

    • 2. 从剩余的子图中任找一回路，同样去掉回路中边权最大的一条边，得一新的子图；

    • 3. 重复第 2 步，直到图中不再含有回路为止。

    • 简洁版

      • 删除回路最大边

  • 最短路问题

    • 最短路问题是指从给定的网络图中找出任意两点之间距离最短（权值和最小）的一条路。 （求从起始点 s 到终止点 t 的最短路径）

    • 狄克斯屈拉( Dijkstra )算法 （标号算法）

      • 定义

        • （两点距离）dij 表示图中两相邻点 i 与 j 的距离

        • （最短距离）Lsi 表示从 s 点到 i 点的最短距离

      • 1. 对起始点 s ，因 Lss =0 ，将 0 标注在 s 旁的小方框内，表示 s 点已标号；

      • 2. 从点 s 出发，找出与 s 相邻的点中距离最小的一个，设为 r ，将 Lsr = Lss+ dsr 的值标注在 r 旁的小方框内，表明点 r 也已标号；

      • 3. 从已标号的点出发，找出与这些点相邻的所有未标号点 p ，若有 Lsp =min { Lss+ dsp , Lsr+ drp }，则对 p 点标号，并将 Lsp 的值标注在 p 点旁的小方框内；

      • 4. 重复第 3 步，直到 t 点得到标号为止。

      • 简洁版

        • 起始点s标0，找与s相邻点距离最小的点 一直标号为该点与s的距离，加粗边 直到标号t

    • 矩阵算法

      • 同时求出所有各点间的最短距离。

      • 步骤

        • 建立距离矩阵

          • 设 dij 表示图中两相邻点 i 与 j 的距离，若 i 与 j 不相邻，令 dij =∞，显然 dii =0。

        • 新矩阵

          • 第n行第m个数据为：第n-1行和第m列依次相加求和取最小

          • 算到有两行数据相同为止，得到最短路。

          • v1到vn的距离为：最后行的第n个数据

        • 画圈找最短路

          • 看最后一行，由于第n行的第m个数据为第n-1行数据和第m列相加取最小，看最小数据在哪里就画圈在哪里

          • 注：自己抵达自己的最短路为0，故不可画圈。

        • lg（p-1）/lg2为计算停止的控制 p为顶点个数

  • 网络的最大流

    • cij

      • 弧的容量，记为c(vi , vj )

    • fij

      • 在弧(vi ,vj )上的负载量记作 f (vi , vj )

    • 增广链

      • 前向弧

        • 所有指向为 s→t 的弧（称前向弧，记作μ+），存在f < c (非饱和)；（正向弧不饱和）

      • 后向弧

        • 所有指向为 t →s 的弧（称后向弧，记为μ -），存在f > 0(非零)，（反向弧非零流）

    • 标号算法 （Ford-Fulkerson）

      • 本质是判断是否存在增广链，如果存在，则找出增广链，调整流量；若不存在，则说明已达到最大流。

      • 第一步：首先给发点 s 标号(0 , ε(s) )。

        • 第一个数字

          • 是使这个点得到标号的前一个点的代号 因 s 是发点，因此记为0。

        • 第二个数字ε(s)

          • 表示从上一个标号到这个标号点的流量的最大允许调整值 s 为发点，不限允许调整容量，故 ε(s)=∞。

      • 第二步：列出与已标号点相邻的所有未标号点

        • 1.考虑从标号点 i 出发的弧 (i ,j )（即正向弧)，如果有 fij=cij，不给点 j 标号；若fij<cij ，则对 j 标号， 记为(i , ε( j ))，其中 ε( j ) = min{ε( i ) ,(cij -fij)}

        • 2.考虑所有指向标号点 i 的弧 (h ,i ) （即反向弧) ，如果有 fhi=0，对 h 不标号， 若 fhi>0，则对 h 点标号，记为(i , ε( h ))，其中ε( h ) = min{ε( i ) , fhi)}.

        • 3.如果某未标号点 k 有两个以上相邻的标号点，可按 (1) ,(2) 中所述规则分别计算出 ε( k )的值，并取其中的最大的一个标记。

      • 第三步：重复第二步可能出现如下两种结果

        • 

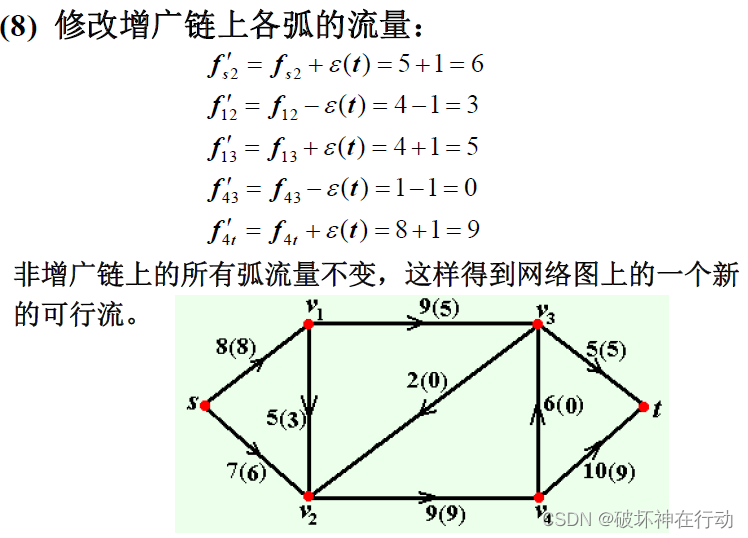
      • 第四步：修改流量

        • 

      • 第五步：抹掉图上所有标号，重复第一到第四步。

      • 简洁版

        • 1、发点标号（0，∞）

        • 2、相邻点标号 （前一点代号， ε(s)或ε( h )）

          • 正向弧用ε(s) ε( j ) = min{ε( i ) ,(cij -fij)}

            • 流量f＜容量c （有增长空间，f-c标号）

            • f = c （无增长空间，不标号）

          • 反向弧用ε( h ) ε( h ) = min{ε( i ) , fhi)}

            • 直接选流量最小的

        • 3、找增广链

          • t未标号，说明无增广链，给定流量为最大流量。

          • t有标号，反向追踪法（从t开始连接标号点）得增广链。

        • 4、修改原流量（正加反减）

          • 正向弧+1，反向弧-1

        • 5、再标号（标号中断）得到可行流

练习题

• 图的最小部分树

• 

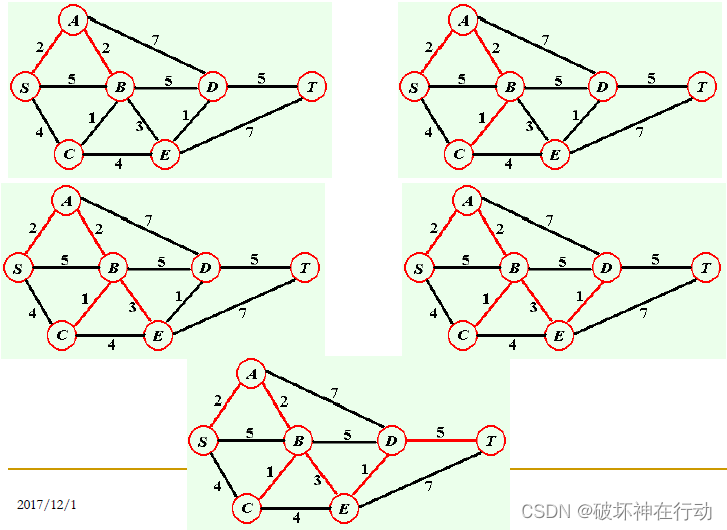
• 避圈法

  • 添加相邻最小边

  • 添加最小边

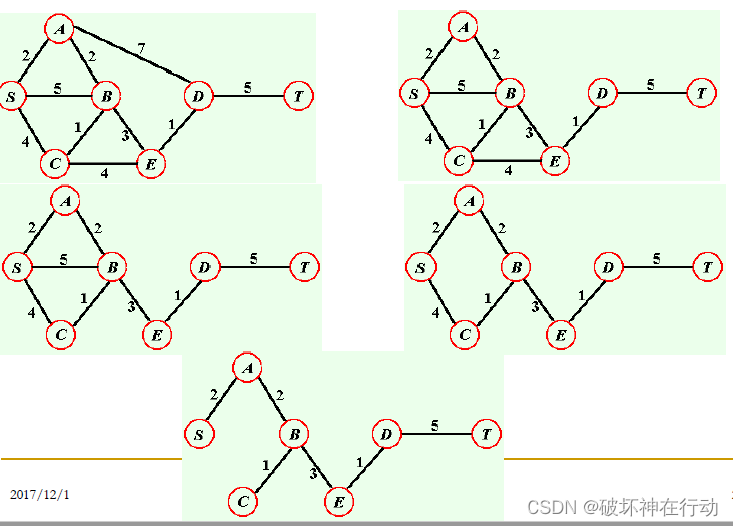
• 破圈法

  • 删除回路最大边

• 最短路问题

• • 

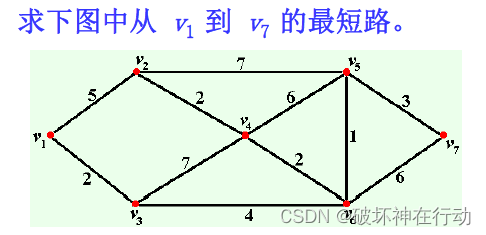
  • 狄克斯屈拉( Dijkstra )算法 （标号算法）

  • 

  • 矩阵算法

  • 

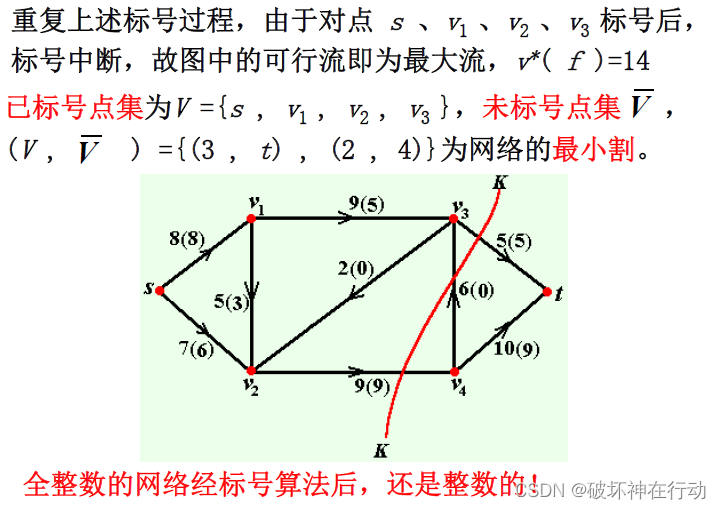
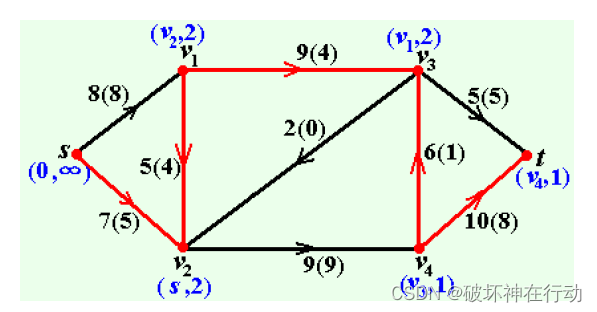
• 网络最大流，最小割

  • 

    •