K-OPT

• replace the notion of one favorable swaps by a search of a favorable sequence of swaps

• do not search for the entire set of sequences but build one incrementally.In fact,it's a process from 2-opt to 3-opt to 4-opt to···and then stop and compare all of these costs and find the best opt.

• find a good k dynamically at a fraction of the cost

• explore a sequence of swaps of increasing sizes

steps:

• choose a vertex and its edge =(,) (cause this edge is long)

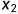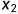• choose an edge =(,) with d()<d()

• if none exist,restart with another vertex

• else,we have a solution by removing the edge (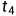,) and connecting (,)

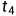• compute the cost but do not connect (still, (,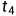) is long)

• instead, we restart the above process with and its pretended edge (,)

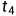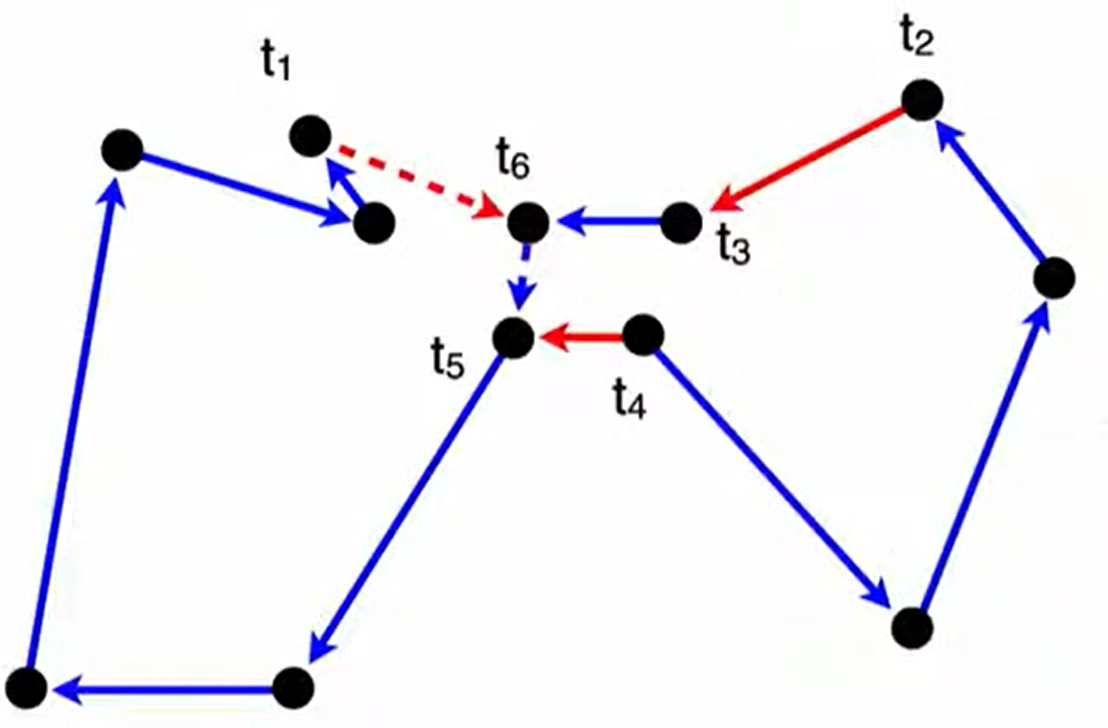
• now it's like 3-opt, but still we don't want to stop here.do the above process (i.e. the k-opt algorithm) again and again and again···

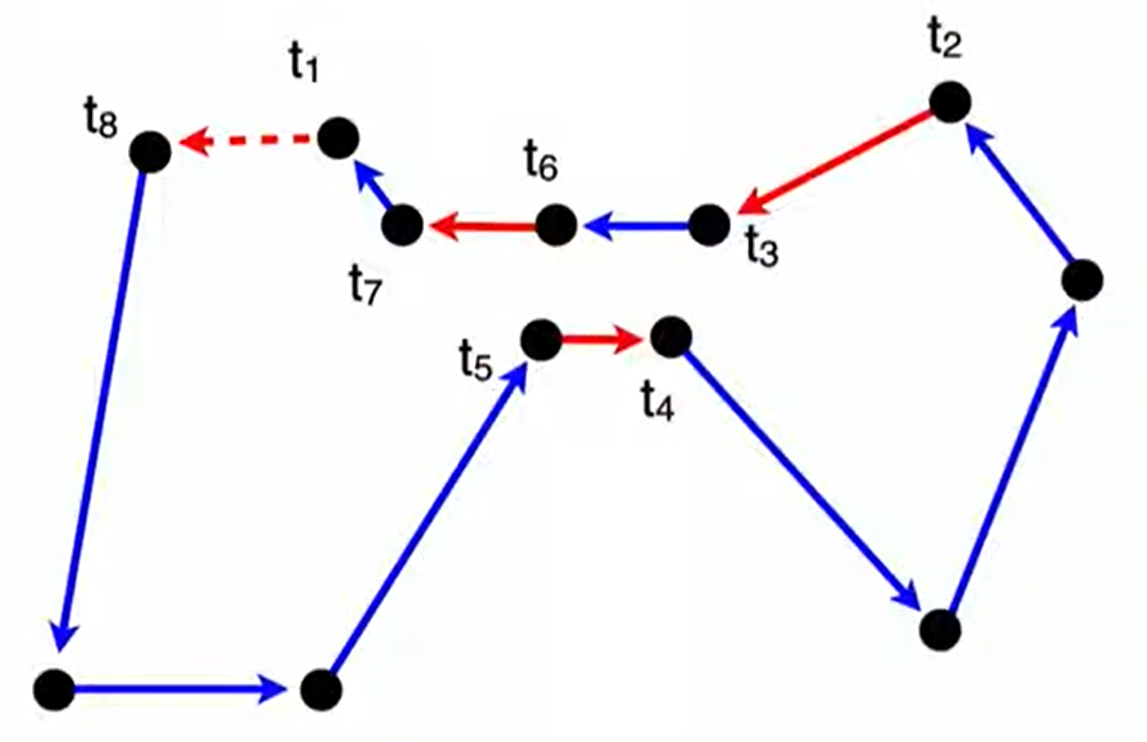
• now it's like 4-opt. And we can stop here to get a good sequence because we can't find a shorter edge from .

• OK,so now we have done our first iteration, we can then choose another vertex and start the second iteration···