密码学系列（二）——数学基础

目录

一、欧几里得算法

二、扩展欧几里得算法

三、模运算

四、欧利定理

五、中国剩余定理

一、欧几里得算法

  欧几里得算法（Euclidean Algorithm）是一种用于计算两个整数的最大公约数的算法。

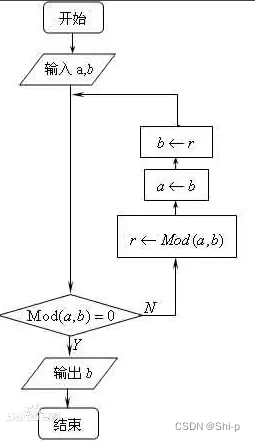
function EuclideanAlgorithm(a, b):
    while b ≠ 0:
        remainder = a mod b
        a = b
        b = remainder
    return a


算法中，a 和 b 是两个非负整数，a mod b 表示 a 除以 b 的余数。
算法通过反复用较小数除较大数，将两个数的大小逐渐减小，直到较小数变成零，
此时较大数就是最大公约数。

例如求103和8 两个正整数的最大公约数,用欧几里得算法表示为：

        103÷8=12（余数为7）

        8÷7=1（余数为1）

        7÷1=7（余数为0）

        由于余数为0，所以最大公约数为1。

因此，103和8的最大公约数为1

二、扩展欧几里得算法

  扩展欧几里得算法是在欧几里得算法的基础上，同时计算最大公约数和两个整数的贝祖等式的算法。贝祖等式表示两个整数 a 和 b 的最大公约数 gcd(a, b) 可以表示成 ax + by 的形式，其中 x 和 y 是整数。

function ExtendedEuclideanAlgorithm(a, b):
    if b == 0:
        return a, 1, 0
    else:
        gcd, x, y = ExtendedEuclideanAlgorithm(b, a mod b)
        return gcd, y, x - (a // b) * y

a 和 b 是两个非负整数，// 表示整数除法。
算法通过递归调用自身，在计算最大公约数的同时，利用贝祖等式的递推关系依次计算出 x 和 y 的值。

三、模运算

  模运算，也称为取模运算或者求余运算，是一种用于计算除法的运算。它计算的结果是除法的余数

模运算通常使用符号 "%" 表示，例如 "a % b" 表示将整数 a 除以 b 并取得余数。

以下是模运算的一些性质：

1. 对于任意整数 a，a % 1 = 0，这是因为任何数除以 1 的余数都为 0。
2. 对于任意整数 a，a % a = 0，这是因为任何数除以自身的余数都为 0。
3. 对于任意整数 a 和正整数 b，如果 a < b，则 a % b = a，这是因为 a 除以 b 的余数就是 a 本身。
4. 对于任意整数 a 和正整数 b，如果 a > b，则 a % b 的余数是小于 b 的非负整数。

假设我们要计算 17 除以 5 的余数，可以使用模运算进行计算。我们将 17 % 5，结果是 2。这意味着当我们将 17 除以 5 时，商为 3，余数为 2。

四、欧利定理

  欧拉定理（Euler's theorem）是数论中的一条重要定理，它建立了数论与模运算之间的联系。欧拉定理是基于欧拉函数的性质而得出的。

欧拉函数 φ(n)（也称为欧拉φ函数）表示小于或等于正整数 n 的数中与 n 互质的数的个数。欧拉函数的计算方法是将 n 分解为质因数的乘积，然后应用一些规则进行计算。

这个定理在密码学领域有广泛应用，特别是在公钥密码体系中。一个典型的例子是 RSA 加密算法。

假设 n = 10，我们要验证欧拉定理。首先，计算 φ(10)。

10 的质因数分解为 2 * 5，因此 φ(10) = (2-1) * (5-1) = 4。

现在，选择与 10 互质的一个正整数 a。我们选择 a = 3。

根据欧拉定理，我们有 3^4 ≡ 1 (mod 10)。

我们可以验证这个等式是否成立，计算 3^4 的结果，并对 10 取模：

3^4 = 81，81 mod 10 = 1。

因此，3^4 ≡ 1 (mod 10) 成立，这符合欧拉定理的要求。

这个例子验证了欧拉定理在模运算中的应用。它说明了选择与 n 互质的 a，在进行模运算时会得到结果为 1。

五、中国剩余定理

  中国剩余定理是用于解决一组同余方程组的问题。它提供了一种有效的方法，可以通过给定一组模数和一组同余方程的余数，求解出一个满足所有同余方程的最小正整数解。

假设我们有一组同余方程：
x ≡ a₁ (mod m₁)
x ≡ a₂ (mod m₂)
...
x ≡ aₙ (mod mₙ)

其中，a₁, a₂, ..., aₙ 是给定的余数，m₁, m₂, ..., mₙ 是互质的模数。

中国剩余定理说明了，如果满足上述条件，那么一定存在一个解 x，且该解在模数 m₁m₂...mₙ 内唯一。

中国剩余定理的一般形式：

假设 m₁, m₂, ..., mₙ 是互质的模数，M = m₁m₂...mₙ，Mᵢ = M/mᵢ（其中 mᵢ = m₁m₂...mₙ/mᵢ），而 Mᵢ 的乘法逆元为 Mᵢ⁻¹（即 Mᵢ * Mᵢ⁻¹ ≡ 1 (mod mᵢ)）。

那么，同余方程组的解 x 可以表示为：
x = (a₁ * M₁ * M₁⁻¹ + a₂ * M₂ * M₂⁻¹ + ... + aₙ * Mₙ * Mₙ⁻¹) mod M

其中，M₁, M₂, ..., Mₙ 分别是 M/m₁, M/m₂, ..., M/mₙ 的值。

解决以下同余方程组：
x ≡ 2 (mod 3)
x ≡ 3 (mod 5)
x ≡ 2 (mod 7)

首先，计算 M = 3 * 5 * 7 = 105。然后计算 M₁ = 105/3 = 35，M₂ = 105/5 = 21，M₃ = 105/7 = 15。

接下来，计算 M₁⁻¹ ≡ 35⁻¹ ≡ 2 (mod 3)，M₂⁻¹ ≡ 21⁻¹ ≡ 1 (mod 5)，M₃⁻¹ ≡ 15⁻¹ ≡ 1 (mod 7)。

然后，根据中国剩余定理的公式计算：
x = (2 * 35 * 2 + 3 * 21 * 1 + 2 * 15 * 1) mod 105
= 140 + 63 + 30 mod 105
= 233 mod 105
= 23

因此，满足给定同余方程组的最小正整数解为 x = 23。

function chinese_remainder_theorem(a[], m[]):
    n = length(a)  // 方程组中的方程数量
    M = 1         // 所有模数的乘积
    for i = 0 to n-1:
        M = M * m[i]
    
    result = 0
    for i = 0 to n-1:
        Mi = M / m[i]                          // Mᵢ = M/mᵢ
        Mi_inverse = modular_inverse(Mi, m[i])  // Mᵢ⁻¹的计算，可以使用扩展欧几里得算法求逆元
        result = result + (a[i] * Mi * Mi_inverse) % M
    
    return result % M

// 求一个数的模逆元
function modular_inverse(a, m):
    g, x, y = extended_euclidean_algorithm(a, m)
    if g != 1:
        // a 不是 m 的乘法逆元，无解
        return ERROR
    else:
        return x % m

// 扩展欧几里得算法
function extended_euclidean_algorithm(a, b):
    if b == 0:
        return a, 1, 0
    else:
        g, x, y = extended_euclidean_algorithm(b, a % b)
        return g, y, x - (a // b) * y