差分隐私-扰动机制

1. 随机响应机制（本地化差分隐私）

原理

在本地差分隐私（LDP）中，每个用户在本地扰动自身数据后再上传，数据收集者无法获知真实值。
核心公式：
对二值数据（如回答“是/否”），用户按以下规则响应：

• 以概率 p回答真实值

• 以概率 1−p随机回答（如抛硬币）

隐私预算 ϵ与 p的关系：

• 经典例子（Warner's Model）： 用户有一个敏感布尔属性（例如是否患病）。用户抛两次硬币：

  • 第一次硬币：如果是正面，则如实回答；如果是反面，则抛第二次硬币并根据第二次的结果回答是或否（随机）。

  • 通过设计第一次硬币正面/反面的概率，可以控制隐私水平（ε）并能在聚合层面从扰动后的数据中无偏地估计真实比例。

实例：

• 适用场景： LDP 场景下收集聚合统计信息（如频率估计、均值、直方图），用户不信任数据收集者。广泛用于浏览器、移动应用收集用户行为统计（如 Google 的 RAPPOR）。

• 变种： 有多种推广形式，如 k-ary 随机响应（处理多个类别）、最优本地哈希（OLH）、分段机制（Piecewise Mechanism）、和谐机制（Harmony Mechanism）等，用于更高效或更精确地处理不同类型的数据和查询。

• 优点： 提供强隐私保证（本地模型），用户完全控制隐私，用户数据在离开设备前已匿名化。实现相对简单。

• 缺点： 要达到与中心化模型相同的精度，通常需要更多的用户（样本量），因为每个用户添加的噪声相对较大。主要适用于聚合统计。

---

2. 拉普拉斯机制（中心化差分隐私）

原理

向数值型查询结果添加拉普拉斯噪声，噪声规模由全局敏感度 Δf和隐私预算ϵ决定：

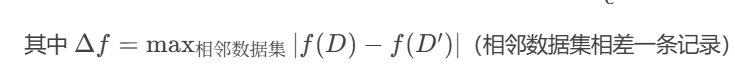
示例：统计医院患者总数

关键点：

• 大查询（如求和）需限制贡献范围（如设定每人最多就诊 5 次 → Δf=5）。

• 满足纯 ϵ-DP，严格无松弛项。

---

3. 高斯噪声机制（中心化差分隐私）

原理

向数值查询添加高斯噪声，提供 (ϵ,δ)-DP 松弛保证：

其中 是 L2 敏感度（相邻数据集查询结果的欧氏距离最大值）。

示例：梯度下降模型训练

场景：训练逻辑回归模型，保护训练样本隐私。

关键优势：

• 高维向量扰动时，高斯噪声的 L2 误差期望更小（比拉普拉斯更适用）。

• 松弛隐私：允许极小概率（δ）违反严格 DP。

---

机制对比与选择指南

机制	适用场景	隐私保证	噪声特点	典型应用
随机响应	本地化、离散数据收集	纯 ϵϵ-LDP	离散扰动	用户行为统计（如RAPPOR）
拉普拉斯	数值查询、小敏感度	纯 ϵϵ-DP	重尾分布	计数、直方图发布
高斯	高维向量、多次查询组合	(ϵ,δ)(ϵ,δ)-DP	集中分布	机器学习梯度保护

选择原则：

• 数据在本地 → 随机响应

• 发布标量值 → 拉普拉斯（严格隐私）或 高斯（需松弛隐私）

• 高维向量（如梯度）→ 高斯机制 + 裁剪

4. 随机响应机制-极大似然估计

在随机响应机制中使用极大似然估计（Maximum Likelihood Estimation, MLE）是为了从扰动后的噪声数据中无偏地还原原始数据的统计特性。