Angular distance

Angular distance {\displaystyle \theta }\theta (also known as angular separation, apparent distance, or apparent separation) is the angle between the two sightlines, or between two point objects as viewed from an observer.

Angular distance appears in mathematics (in particular geometry and trigonometry) and all natural sciences (e.g. astronomy and geophysics). In the classical mechanics of rotating objects, it appears alongside angular velocity, angular acceleration, angular momentum, moment of inertia and torque.

1 Use

The term angular distance (or separation) is technically synonymous with angle itself, but is meant to suggest the linear distance between objects (for instance, a couple of stars observed from Earth).

2 Measurement

Since the angular distance (or separation) is conceptually identical to an angle, it is measured in the same units, such as degrees or radians, using instruments such as goniometers or optical instruments specially designed to point in well-defined directions and record the corresponding angles (such as telescopes).

3 Equation

3.1 General case

To derive the equation that describes the angular separation of two points located on the surface of a sphere as seen from the center of the sphere, we use the example of two astronomical objects {\displaystyle A}A and {\displaystyle B}B observed from the Earth. The objects {\displaystyle A}A and {\displaystyle B}B are defined by their celestial coordinates, namely their right ascensions (RA), {\displaystyle (\alpha _{A},\alpha _{B})\in [0,2\pi ]}{\displaystyle (\alpha _{A},\alpha _{B})\in [0,2\pi ]}; and declinations (dec), {\displaystyle (\delta _{A},\delta _{B})\in [-\pi /2,\pi /2]}{\displaystyle (\delta _{A},\delta _{B})\in [-\pi /2,\pi /2]}. Let {\displaystyle O}O indicate the observer on Earth, assumed to be located at the center of the celestial sphere. The dot product of the vectors {\displaystyle \mathbf {OA} }{\displaystyle \mathbf {OA} } and {\displaystyle \mathbf {OB} }{\displaystyle \mathbf {OB} } is equal to:

{\displaystyle \mathbf {OA} \cdot \mathbf {OB} =R^{2}\cos \theta }{\displaystyle \mathbf {OA} \cdot \mathbf {OB} =R^{2}\cos \theta }
which is equivalent to:

{\displaystyle \mathbf {n_{A}} .\mathbf {n_{B}} =\cos \theta }{\displaystyle \mathbf {n_{A}} .\mathbf {n_{B}} =\cos \theta }
In the {\displaystyle (x,y,z)}(x,y,z) frame, the two unitary vectors are decomposed into:

{\displaystyle \mathbf {n_{A}} ={\begin{pmatrix}\cos \delta _{A}\cos \alpha _{A}\\cos \delta _{A}\sin \alpha _{A}\\sin \delta {A}\end{pmatrix}}\mathrm {\qquad and\qquad } \mathbf {n{B}} ={\begin{pmatrix}\cos \delta _{B}\cos \alpha _{B}\\cos \delta _{B}\sin \alpha _{B}\\sin \delta {B}\end{pmatrix}}.}{\displaystyle \mathbf {n{A}} ={\begin{pmatrix}\cos \delta _{A}\cos \alpha _{A}\\cos \delta _{A}\sin \alpha _{A}\\sin \delta {A}\end{pmatrix}}\mathrm {\qquad and\qquad } \mathbf {n{B}} ={\begin{pmatrix}\cos \delta _{B}\cos \alpha _{B}\\cos \delta _{B}\sin \alpha _{B}\\sin \delta _{B}\end{pmatrix}}.}
Therefore,

{\displaystyle \mathbf {n_{A}} \mathbf {n_{B}} =\cos \delta _{A}\cos \alpha _{A}\cos \delta _{B}\cos \alpha _{B}+\cos \delta _{A}\sin \alpha _{A}\cos \delta _{B}\sin \alpha _{B}+\sin \delta {A}\sin \delta {B}\equiv \cos \theta }{\displaystyle \mathbf {n{A}} \mathbf {n{B}} =\cos \delta _{A}\cos \alpha _{A}\cos \delta _{B}\cos \alpha _{B}+\cos \delta _{A}\sin \alpha _{A}\cos \delta _{B}\sin \alpha _{B}+\sin \delta _{A}\sin \delta _{B}\equiv \cos \theta }
then:

{\displaystyle \theta =\cos ^{-1}\left[\sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\cos(\alpha _{A}-\alpha _{B})\right]}{\displaystyle \theta =\cos ^{-1}\left[\sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\cos(\alpha _{A}-\alpha _{B})\right]}

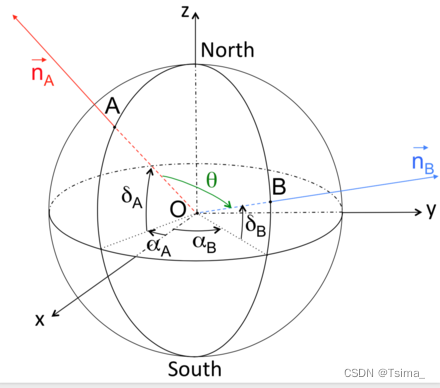
Angular separation {\displaystyle \theta }\theta between points A and B as seen from O

3.2 Small angular distance approximation

The above expression is valid for any position of A and B on the sphere. In astronomy, it often happens that the considered objects are really close in the sky: stars in a telescope field of view, binary stars, the satellites of the giant planets of the solar system, etc. In the case where {\displaystyle \theta \ll 1}{\displaystyle \theta \ll 1} radian, implying {\displaystyle \alpha _{A}-\alpha _{B}\ll 1}{\displaystyle \alpha _{A}-\alpha _{B}\ll 1} and {\displaystyle \delta _{A}-\delta _{B}\ll 1}{\displaystyle \delta _{A}-\delta _{B}\ll 1}, we can develop the above expression and simplify it. In the small-angle approximation, at second order, the above expression becomes:

{\displaystyle \cos \theta \approx 1-{\frac {\theta ^{2}}{2}}\approx \sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\left[1-{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}\right]}{\displaystyle \cos \theta \approx 1-{\frac {\theta ^{2}}{2}}\approx \sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\left[1-{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}\right]}
meaning

{\displaystyle 1-{\frac {\theta ^{2}}{2}}\approx \cos(\delta _{A}-\delta _{B})-\cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}}{\displaystyle 1-{\frac {\theta ^{2}}{2}}\approx \cos(\delta _{A}-\delta _{B})-\cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}}
hence

{\displaystyle 1-{\frac {\theta ^{2}}{2}}\approx 1-{\frac {(\delta _{A}-\delta _{B})^{2}}{2}}-\cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}}{\displaystyle 1-{\frac {\theta ^{2}}{2}}\approx 1-{\frac {(\delta _{A}-\delta _{B})^{2}}{2}}-\cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}}.
Given that {\displaystyle \delta _{A}-\delta _{B}\ll 1}{\displaystyle \delta _{A}-\delta _{B}\ll 1} and {\displaystyle \alpha _{A}-\alpha _{B}\ll 1}{\displaystyle \alpha _{A}-\alpha _{B}\ll 1}, at a second-order development it turns that {\displaystyle \cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}\approx \cos ^{2}\delta _{A}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}}{\displaystyle \cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}\approx \cos ^{2}\delta _{A}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}}, so that

{\displaystyle \theta \approx {\sqrt {\left[(\alpha _{A}-\alpha _{B})\cos \delta _{A}\right]^{2}+(\delta _{A}-\delta _{B})^{2}}}}{\displaystyle \theta \approx {\sqrt {\left[(\alpha _{A}-\alpha _{B})\cos \delta _{A}\right]^{2}+(\delta _{A}-\delta _{B})^{2}}}}

3.3 Small angular distance: planar approximation

If we consider a detector imaging a small sky field (dimension much less than one radian) with the {\displaystyle y}y-axis pointing up, parallel to the meridian of right ascension {\displaystyle \alpha }\alpha , and the {\displaystyle x}x-axis along the parallel of declination {\displaystyle \delta }\delta , the angular separation can be written as:

{\displaystyle \theta \approx {\sqrt {\delta x^{2}+\delta y^{2}}}}{\displaystyle \theta \approx {\sqrt {\delta x^{2}+\delta y^{2}}}}
where {\displaystyle \delta x=(\alpha _{A}-\alpha _{B})\cos \delta _{A}}{\displaystyle \delta x=(\alpha _{A}-\alpha _{B})\cos \delta _{A}} and {\displaystyle \delta y=\delta _{A}-\delta _{B}}{\displaystyle \delta y=\delta _{A}-\delta _{B}}.

Note that the {\displaystyle y}y-axis is equal to the declination, whereas the {\displaystyle x}x-axis is the right ascension modulated by {\displaystyle \cos \delta _{A}}{\displaystyle \cos \delta _{A}} because the section of a sphere of radius {\displaystyle R}R at declination (latitude) {\displaystyle \delta }\delta is {\displaystyle R’=R\cos \delta _{A}}{\displaystyle R’=R\cos \delta _{A}} (see Figure).

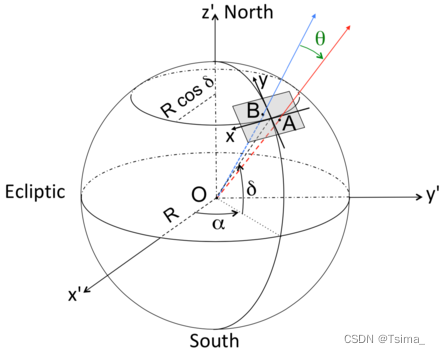
Planar approximation of angular distance on sky

4 See also

Milliradian
Gradian
Hour angle
Central angle
Angle of rotation
Angular diameter
Angular displacement
Great-circle distance
Cosine similarity § Angular distance and similarity