最小二乘法

定义模型
表达式: f θ ( x ) = θ 0 + θ 1 x f_\theta(x)=\theta_0+\theta_1x fθ(x)=θ0+θ1x
(常用 θ \theta θ表示未知数、 f θ ( x ) f_\theta(x) fθ(x)表示含有参数 θ \theta θ并且和变量 x x x相关的函数)
目标函数
假设有 n n n个训练数据,那么它们的误差之和可以这样表示,这个表达式称为目标函数。
E ( θ ) = 1 2 ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) ) 2 E(\theta)=\frac12\sum\limits_{i=1}^n(y^{(i)}-f_\theta(x^{(i)}))^2 E(θ)=21i=1∑n(y(i)−fθ(x(i)))2 ( x ( i ) 和 y ( i ) x^{(i)}和y^{(i)} x(i)和y(i)指第 i i i个训练数据)
找到使 E ( θ ) E(\theta) E(θ)值最小的 θ \theta θ,这样的问题称为最优化问题。
为了避免正负数混合运算所以计算平方, 1 2 \frac12 21是为了让表达式值更简单随便加的常数。
设 θ 0 = 1 、 θ 1 = 3 \theta_0=1、\theta_1=3 θ0=1、θ1=3,将四个训练数据带入表达式求误差如下:
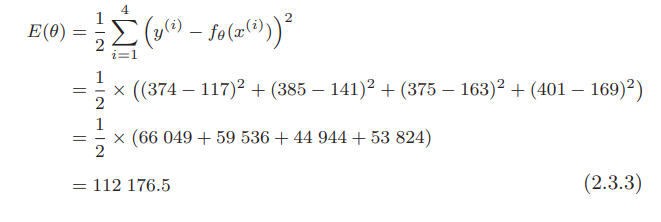
修改参数 θ \theta θ的值,让误差变小的做法称为最小二乘法。
最速下降法
比如表达式 g ( x ) = ( x − 1 ) 2 g(x)=(x-1)^2 g(x)=(x−1)2,它的最小值 g ( x ) = 0 g(x)=0 g(x)=0出现在 x = 1 x=1 x=1时。
图像如下:
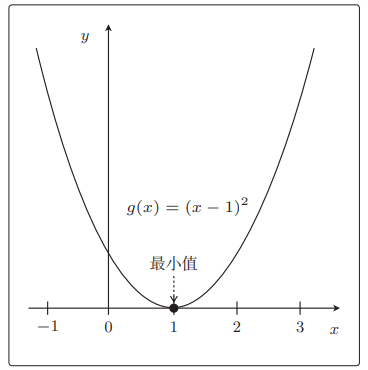
g ( x ) g(x) g(x)展开有 ( x − 1 ) 2 = x 2 − 2 x + 1 (x-1)^2=x^2-2x+1 (x−1)2=x2−2x+1
微分有: d d x g ( x ) = 2 x − 2 \frac{d}{dx}g(x)=2x-2 dxdg(x)=2x−2
为了让 g ( x ) g(x) g(x)的值变小,要让 x x x向1移动,可以根据导数符号决定 x x x的移动方向,只要向着导数符号相反的方向移动 x x x, g ( x ) g(x) g(x)就会向着最小值移动。
由此得到表达式
x : = x − η d d x g ( x ) x:=x-\eta\frac{d}{dx}g(x) x:=x−ηdxdg(x) 称为最速下降法或梯度下降法。
(A:=B,意思通过B来定义A,上面表达式指用上一个x来定义新的x)
η \eta η是称为学习率的正常数,大小会影响达到最小值的更新次数,太大会导致来回跳跃无法收敛,一直发散状态。
对于目标函数, E ( θ ) = 1 2 ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) ) 2 E(\theta)=\frac12\sum\limits_{i=1}^n(y^{(i)}-f_\theta(x^{(i)}))^2 E(θ)=21i=1∑n(y(i)−fθ(x(i)))2 有两个参数,要用偏微分。
( f θ ( x ) = θ 0 + θ 1 x f_\theta(x)=\theta_0+\theta_1x fθ(x)=θ0+θ1x)
更新表达式如下:
θ 0 : = θ 0 − η ∂ E ∂ θ 0 \theta_0:=\theta_0-\eta\frac{\partial E}{\partial\theta_0} θ0:=θ0−η∂θ0∂E
θ 1 : = θ 1 − η ∂ E ∂ θ 1 \theta_1:=\theta_1-\eta\frac{\partial E}{\partial\theta_1} θ1:=θ1−η∂θ1∂E
∂ E ∂ θ 0 = ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) \frac{\partial E}{\partial\theta_0}=\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)}) ∂θ0∂E=i=1∑n(fθ(x(i))−y(i))
∂ E ∂ θ 1 = ∂ E ∂ θ 0 = ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) \frac{\partial E}{\partial\theta_1}=\frac{\partial E}{\partial\theta_0}=\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x^{(i)} ∂θ1∂E=∂θ0∂E=i=1∑n(fθ(x(i))−y(i))x(i)
所以得到参数 θ 1 和 θ 2 \theta_1和\theta_2 θ1和θ2的更新表达式如下:
θ 0 : = θ 0 − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) \theta_0:=\theta_0-\eta\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)}) θ0:=θ0−ηi=1∑n(fθ(x(i))−y(i))
θ 1 : = θ 1 − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) \theta_1:=\theta_1-\eta\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x^{(i)} θ1:=θ1−ηi=1∑n(fθ(x(i))−y(i))x(i)
多项式回归
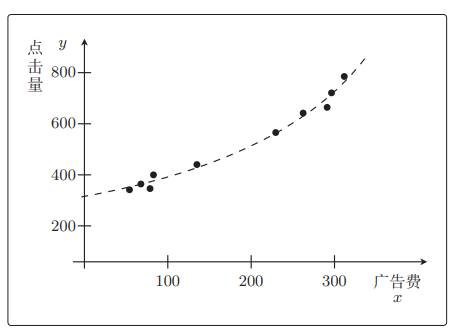
曲线比直线更容易拟合数据
把 f θ ( x ) f_\theta(x) fθ(x)定义为二次函数:
f θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 f_\theta(x)=\theta_0+\theta_1x+\theta_2x^2 fθ(x)=θ0+θ1x+θ2x2
或者更大次数的表达式:
f θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 + . . . + θ n x n f_\theta(x)=\theta_0+\theta_1x+\theta_2x^2+...+\theta_nx^n fθ(x)=θ0+θ1x+θ2x2+...+θnxn
如 f θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 f_\theta(x)=\theta_0+\theta_1x+\theta_2x^2 fθ(x)=θ0+θ1x+θ2x2
得到更新表达式为:
θ 0 : = θ 0 − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) \theta_0:=\theta_0-\eta\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)}) θ0:=θ0−ηi=1∑n(fθ(x(i))−y(i))
θ 1 : = θ 1 − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) \theta_1:=\theta_1-\eta\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x^{(i)} θ1:=θ1−ηi=1∑n(fθ(x(i))−y(i))x(i)
θ 2 : = θ 2 − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x ( i ) 2 \theta_2:=\theta_2-\eta\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x^{(i)^2} θ2:=θ2−ηi=1∑n(fθ(x(i))−y(i))x(i)2
这种增加函数中多项式的次数,再使用函数的分析方法被称为多项式回归。
多重回归
问题:基于广告费预测点击率
考虑广告版面的大小,设 广告费为 x 1 x_1 x1、广告栏的宽为 x 2 x_2 x2、广告栏的高为 x 3 x_3 x3
f θ f_\theta fθ可以表示如下:
f θ ( x 1 , x 2 , x 3 ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 f_\theta(x_1,x_2,x_3)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3 fθ(x1,x2,x3)=θ0+θ1x1+θ2x2+θ3x3
简化表达式,将 θ 和 x \theta和x θ和x看成向量
θ = [ θ 0 θ 1 θ 2 ⋮ θ n ] \boldsymbol{\theta}=\begin{bmatrix} \theta_0\\\theta_1\\\theta_2\\\vdots\\\theta_n \end{bmatrix} θ= θ0θ1θ2⋮θn x = [ x 0 x 1 x 2 ⋮ x n ] \boldsymbol{x}=\begin{bmatrix}x_0\\x_1\\x_2\\\vdots\\x_n \end{bmatrix} x= x0x1x2⋮xn ( x 0 = 1 x_0=1 x0=1)
θ T x = θ 0 x 0 + θ 1 x 1 + . . . + θ n x n \boldsymbol{\theta}^T\boldsymbol{x}=\theta_0x_0+\theta_1x_1+...+\theta_nx_n θTx=θ0x0+θ1x1+...+θnxn
E ( θ ) = 1 2 ∑ i = 1 n ( f θ ( x ( i ) − y ( i ) ) ) 2 E(\theta)=\frac12\sum\limits_{i=1}^n(f_\theta(x^{(i)}-y^{(i)}))^2 E(θ)=21i=1∑n(fθ(x(i)−y(i)))2
∂ E ∂ θ j = ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial E}{\partial\theta_j}=\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)} ∂θj∂E=i=1∑n(fθ(x(i))−y(i))xj(i)
θ j : = θ j − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\eta\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−ηi=1∑n(fθ(x(i))−y(i))xj(i)
像这样包含多个变量的回归称为多重回归
随机梯度下降法
最速下降法容易陷入局部最优解
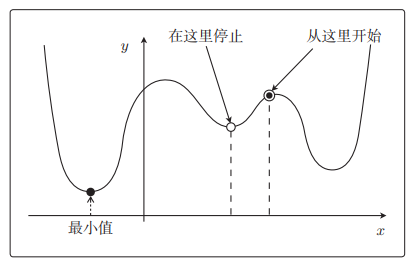
最速下降法更新表达式: θ j : = θ j − η ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\eta\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−ηi=1∑n(fθ(x(i))−y(i))xj(i)
随机梯度下降法中会随机选择一个训练数据,并使用它来更新参数。这个表达式中的 k k k就是被随机选中的数据索引。
随机梯度下降法更新表达式: θ j : = θ j − η ( f θ ( x ( k ) ) − y ( k ) ) x j ( k ) \theta_j:=\theta_j-\eta(f_\theta(x^{(k)})-y^{(k)})x_j^{(k)} θj:=θj−η(fθ(x(k))−y(k))xj(k)
最速下降法更新1次参数的时间,随机梯度下降法可以更新n次,这样不容易陷入局部最优解。
小批量梯度下降法
设训练数据索引的集合为 K K K,还可以随机选择m个训练数据来更新参数。
小批量梯度下降法更新表达式: θ j : = θ j − η ∑ k ∈ K ( f θ ( x ( k ) ) − y ( k ) ) x j ( k ) \theta_j:=\theta_j-\eta\sum\limits_{k\in K}(f_\theta(x^{(k)})-y^{(k)})x_j^{(k)} θj:=θj−ηk∈K∑(fθ(x(k))−y(k))xj(k)
练数据索引的集合为 K K K,还可以随机选择m个训练数据来更新参数。
小批量梯度下降法更新表达式: θ j : = θ j − η ∑ k ∈ K ( f θ ( x ( k ) ) − y ( k ) ) x j ( k ) \theta_j:=\theta_j-\eta\sum\limits_{k\in K}(f_\theta(x^{(k)})-y^{(k)})x_j^{(k)} θj:=θj−ηk∈K∑(fθ(x(k))−y(k))xj(k)






















 119
119











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








