超参数调试、Batch正则化和tensorflow框架

一、超参数调试

1.1 超参数调试的基本思想

神经网络的改变会涉及到许多不同超参数的设置。关于训练深度最难的事情之一是你要处理的参数的数量，从学习速率𝑎到 Momentum （动量梯度下降法）的参数𝛽。如果使用 Momentum 或 Adam 优化算法的参数，𝛽1，𝛽2和𝜀， 也许你还得选择层数，也许你还得选择不同层中隐藏单元的数量，也许你还想使用学习率衰减。所以，你使用的不是单一的学习率𝑎。接着，当然你可能还需要选择 mini-batch 的大小。 结果证实一些超参数比其它的更为重要，学习率是需要调试的最重要的超参数。 还有一些参数需要调试，例如 Momentum 参数𝛽，0.9 就是个很好的默认值。我还会调试 mini-batch 的大小，以确保最优算法运行有效等等，在模型训练过程中根据我们使用的算法，我们需要调试各种各样的参数。

当我们事先不知道哪些超参数更加重要时，对于超参数的取值我们常常是均匀或者随机采样。总的来说，我们需要对超参数形成的空间进行采样，不断调试这些参数。如下图所示：

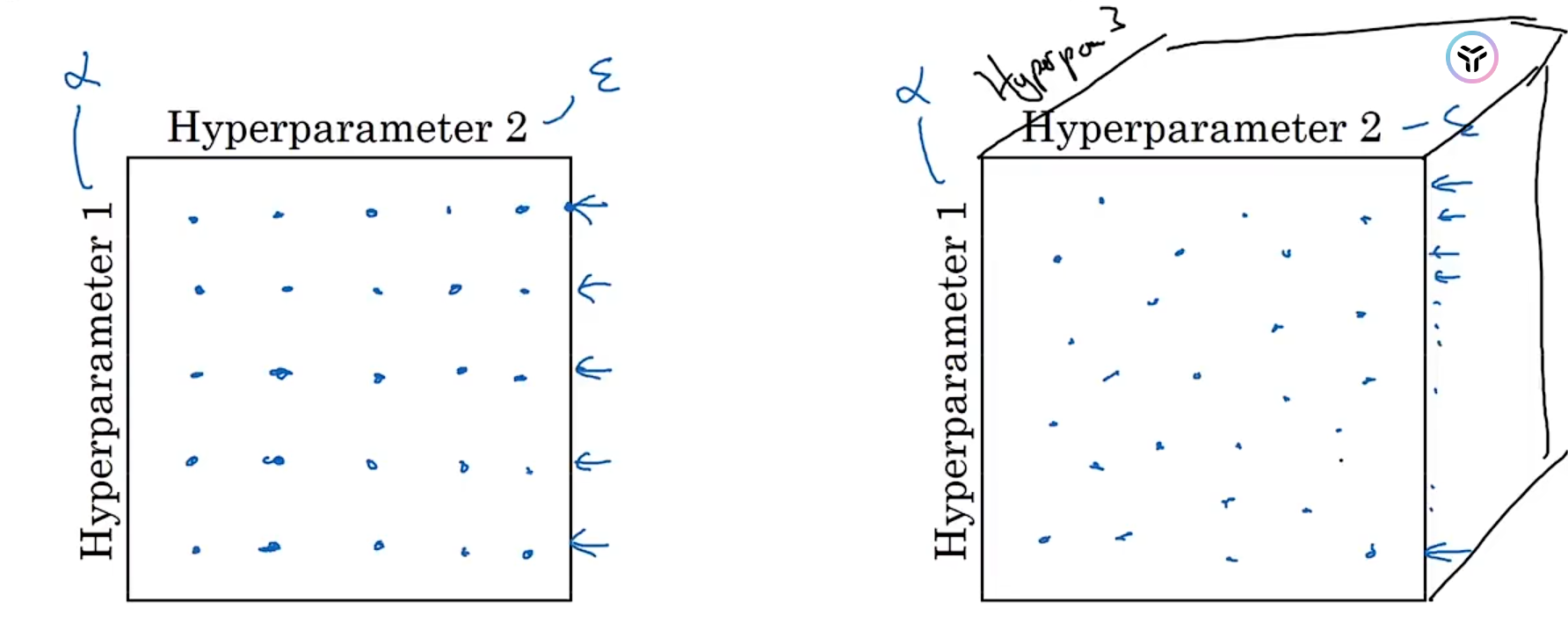
在空间中搜索参数的值时，我们常常采用从粗到细的搜索策略，从一个大区域里面采样，如果某个区域表现好，我们则缩放到该区域再次进行采样以更好地优化参数。

1.2 为超参数选择合适的范围

在超参数范围中，随机取值可以提升你的搜索效率。但随机取值并不是在有效范围内的随机均匀取值，而是选择合适的标尺，用于探究这些超参数，这很重要。

所以，如果你想研究更多正式的数学证明，关于为什么我们要这样做，为什么用线性轴取值不是个好办法，这是因为当𝛽 接近 1 时，所得结果的灵敏度会变化，即使𝛽有微小的变化。所以𝛽 在 0.9 到 0.9005 之间取值，无关紧要，你的结果几乎不会变化。

1.3 超参数训练的实践

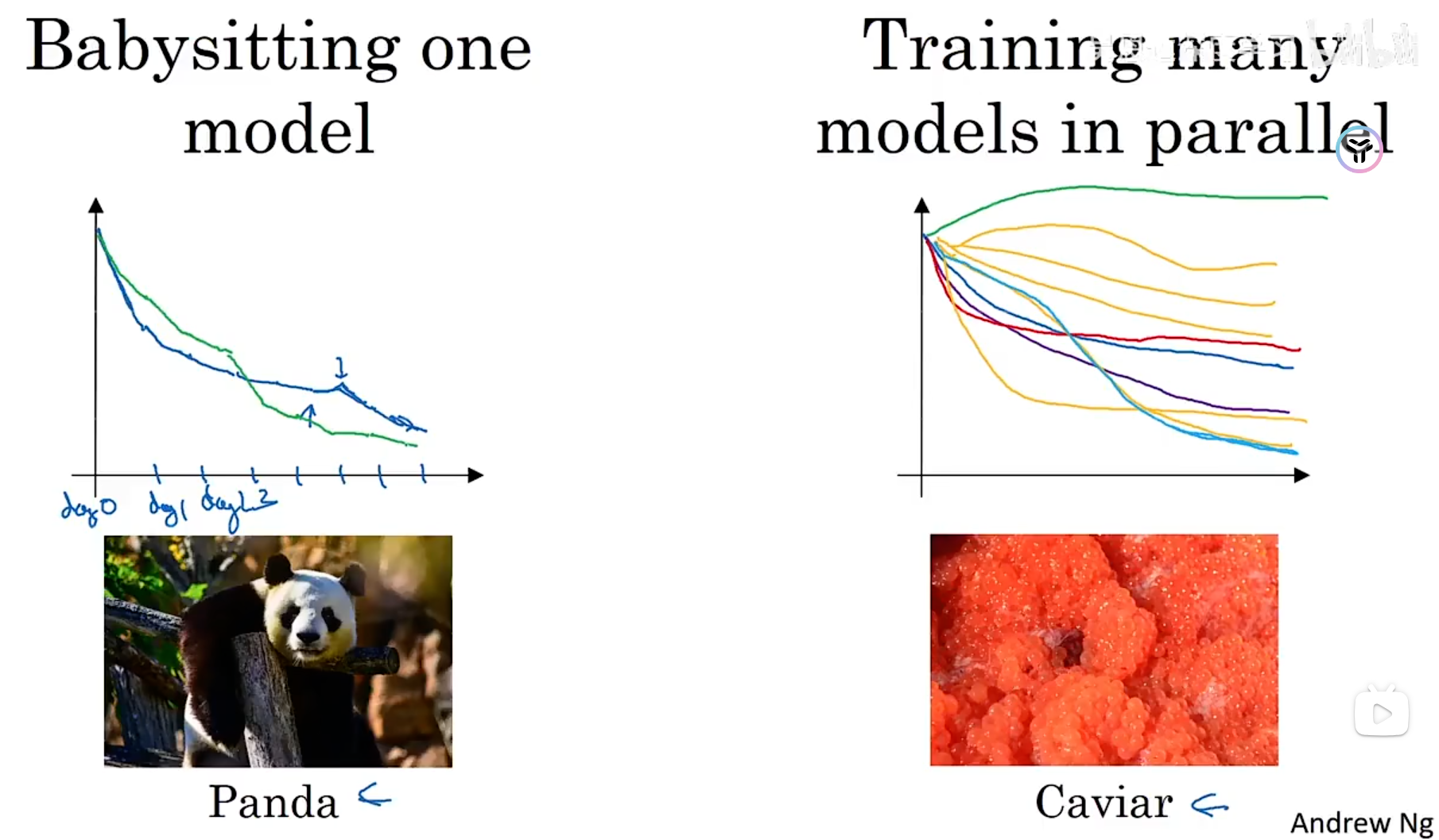
这里提出了两种超参数调试的过程，我们可以根据自己的算力来决定用哪一个，第一种叫做熊猫策略：一次只训练一个模型（没有许多计算资源或足够的 CPU 和 GPU 的前提），只是在不同的阶段调试不同的参数，根据调整的结果不断地进行优化，过程更加细致。第二个调试方式是鱼子酱策略，同时训练多个模型，每一个模型调整不同的参数，观察哪个模型的效果最好。

二、批量归一化

2.1 批量归一化的思想

总所周知，归一化输入特征可以加速学习。

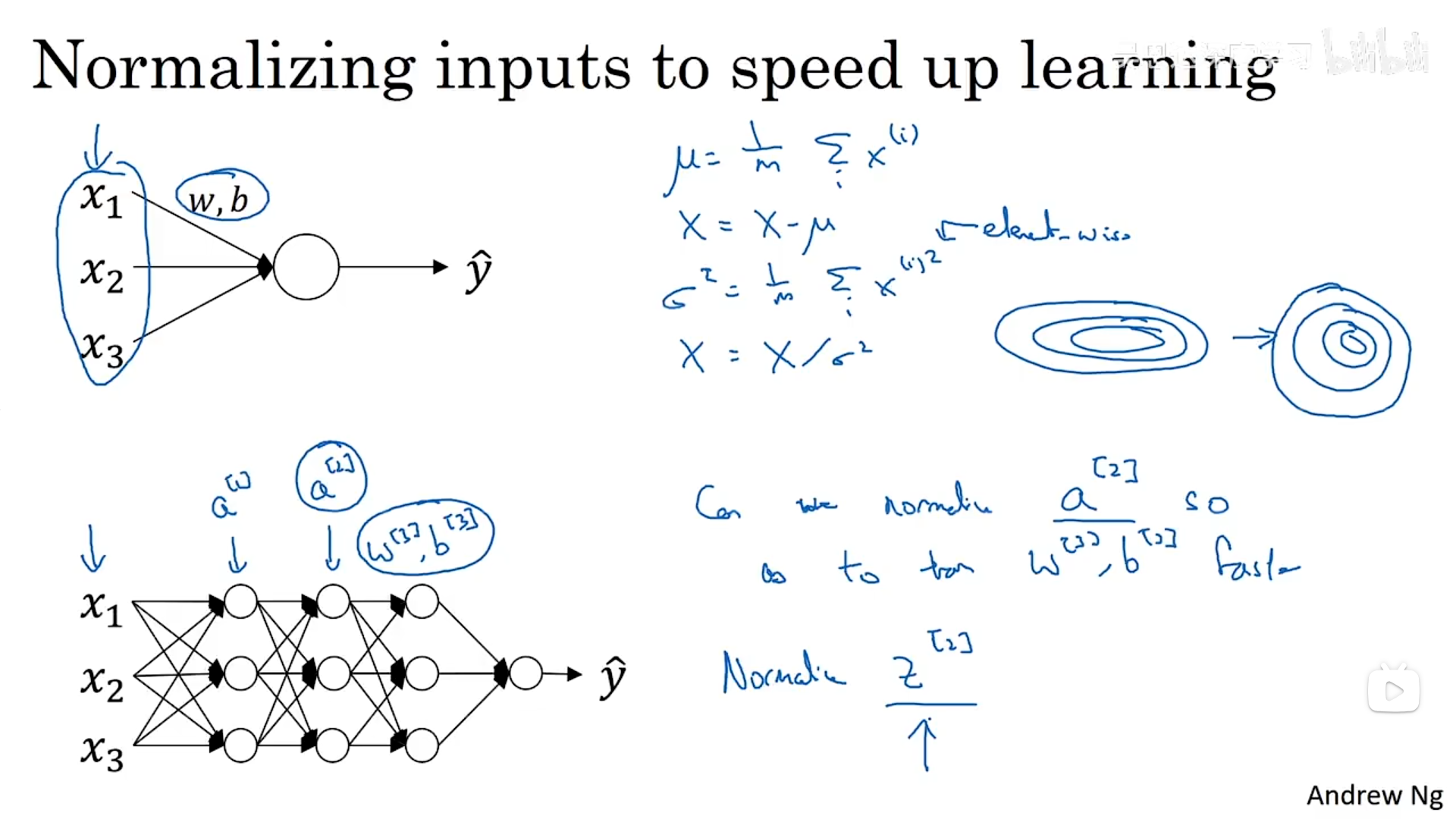在逻辑回归中我们可以使用归一化对数据集进行处理，这样梯度下降的过程就会加快，同样，在神经网络中，我们也可以对各个隐藏层进行归一化，哪是对a还是对z呢？那么实际上我们将归一化z的值而不是a的值。究竟应该归一化哪个值，目前还存在争议（目前归一化z的值更多）。

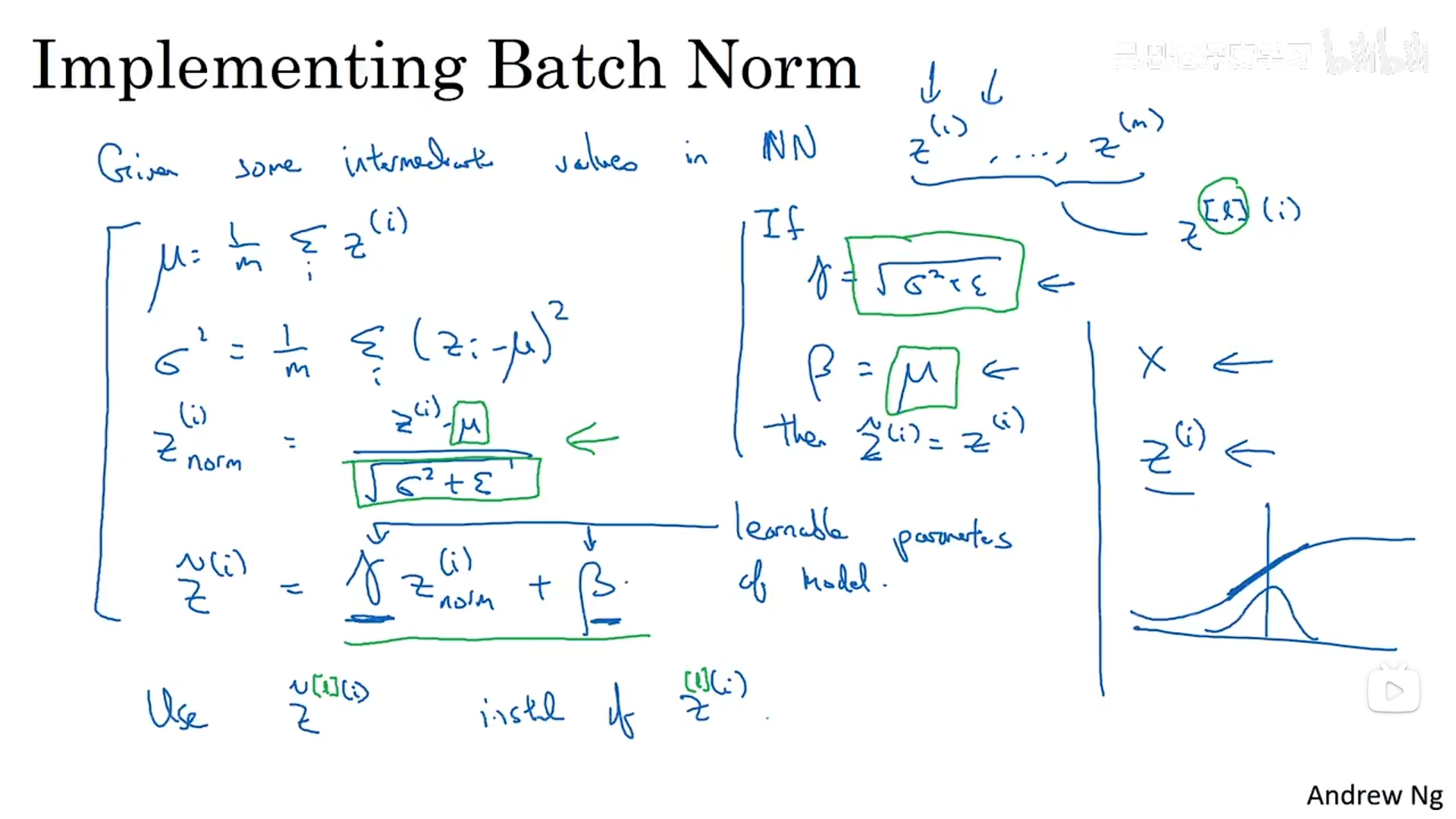
同样的方法，我们也可以对神经网络中的某一层隐藏层进行归一化，将所有数据对应的z的值-均值/标准差，这里在里面加入一个epsilon是为了保证数据的稳定性。这样就将z归一化为均值为0，方差为1的数据。但是所有的隐藏层不可能都是均值为0，方差为1的数据，隐藏单元有不同分布才更有意义，因此我们将计算称为z tilde的值。

2.2 批量归一化融入深度神经网络

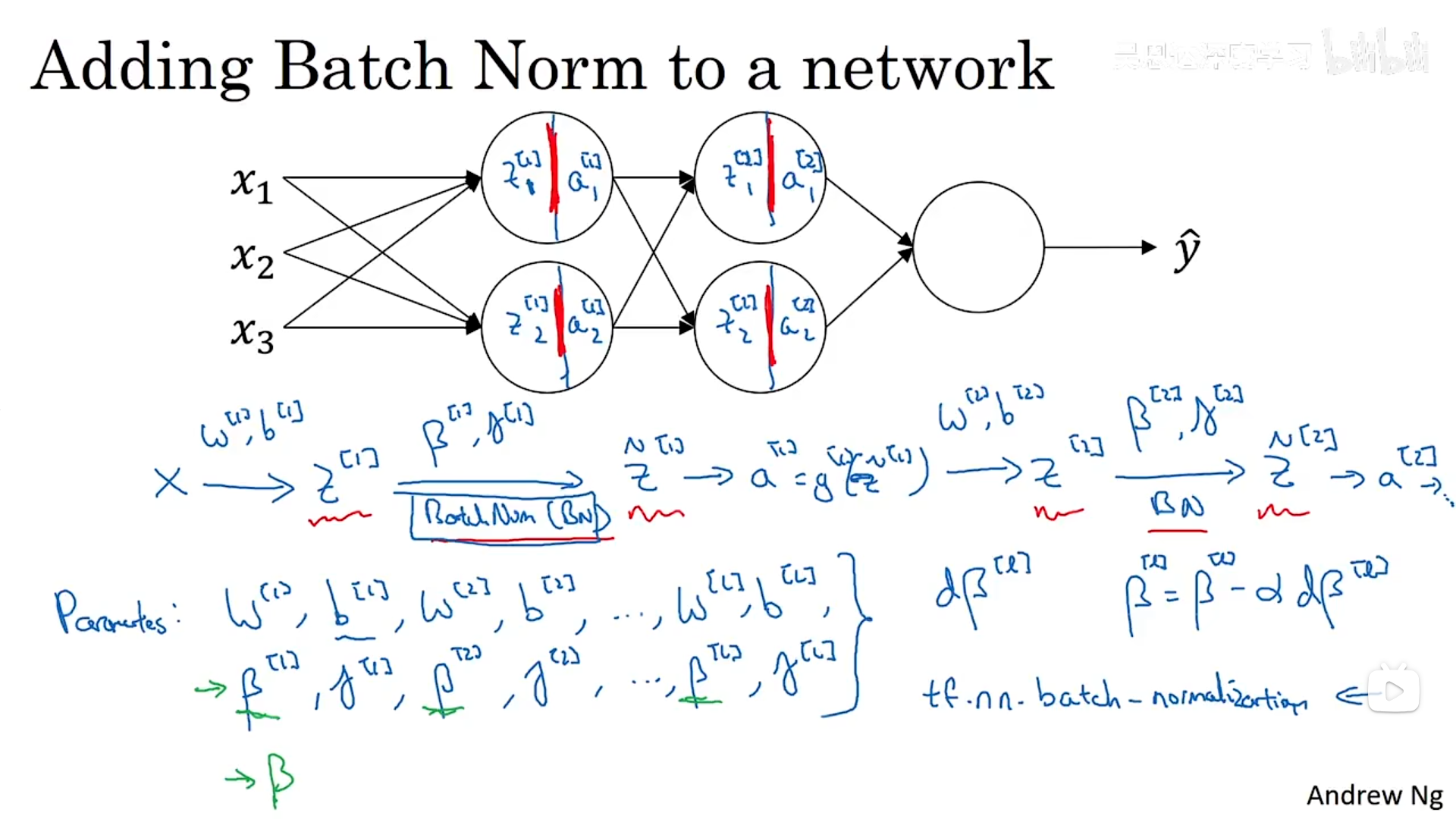
批量归一化通常与训练集中的小批量一起使用。

如果你已将梯度计算如下，你就可以使用梯度下降法了，这就是我写到这里的，但也适 用于有 Momentum、RMSprop、Adam 的梯度下降法。与其使用梯度下降法更新 mini-batch， 你可以使用这些其它算法来更新，我们在之前几个星期中的视频中讨论过的，也可以应用其 它的一些优化算法来更新由 Batch 归一化添加到算法中的𝛽 和𝛾 参数。接下来，我们将所有东西放在一起，描述一下如何使用批量归一化实现梯度下降。

2.3 为什么批量归一化有效

协变量迁移：如果已经学习了某些x到y的映射，如果x的分布发生变化，那么我们可能需要重新训练我们的模型，即使从x到y的底层真实函数保持不变。如下所示：

协变量偏移如何影响神经网络呢？当数据集发生改变时，我们计算出的a也会发生改变，隐藏单元的值也在发生改变，这就发生了协变量偏移的问题。那我们的批量归一化是如何处理的呢？它减少了隐藏单元值分布的变化量，批量归一化保证我们的数据无论如何变化，归一化后的z的均值和方差保持不变。因此批量归一化减少了输入值变化的问题，真正改变这些值使其更稳定，它减弱了早期层参数必须做的与后续层参数必须做的之间的耦合。

事实证明批量归一化具有一定的正则化效果，因为我们是在小批量的数据上进行均值和方差的缩放，与整体数据有一定的偏差，具有噪声，另外从z到z tidle的缩放过程也是具有一定的噪声的，因为它使用稍微有点噪声的均值和方差计算的。类似于dropout，它为每一隐藏层添加了一些噪声（按照一定的概率取消某一个神经单元——乘法噪声），批量归一化具有乘法噪声（/标准差）和加法噪声（-均值），批量归一化因此有轻微的正则化效果，因想隐藏单元添加噪声，迫使下游隐藏单元不要过度依赖任一隐藏单元。

2.4 测试时的批量归一化

我们在使用批量归一化时，是一小批量地处理数据，然而在测试时，我们常常需要逐个处理示例。批量归一化处理过程中需要计算小批量地均值和方差，那么对于单一测试样例应该怎么做呢？我们需要另外一种方法来计算均值和方差。

在实际操作中，我们通常运用指数加权平均来追踪在训练过程中你看到的𝜇和𝜎2的值。还可以用指数加权平均，有时也叫做流动平均来粗略估算𝜇和𝜎2，然后在测试中使用𝜇和𝜎2的值来进行你所需要的隐藏单元𝑧值的调整。

三、softmax回归（识别多个类别）

3.1 softmax的基本思想

示例如下所示，输出的是四个特征，分别对应着4个类别的概率。

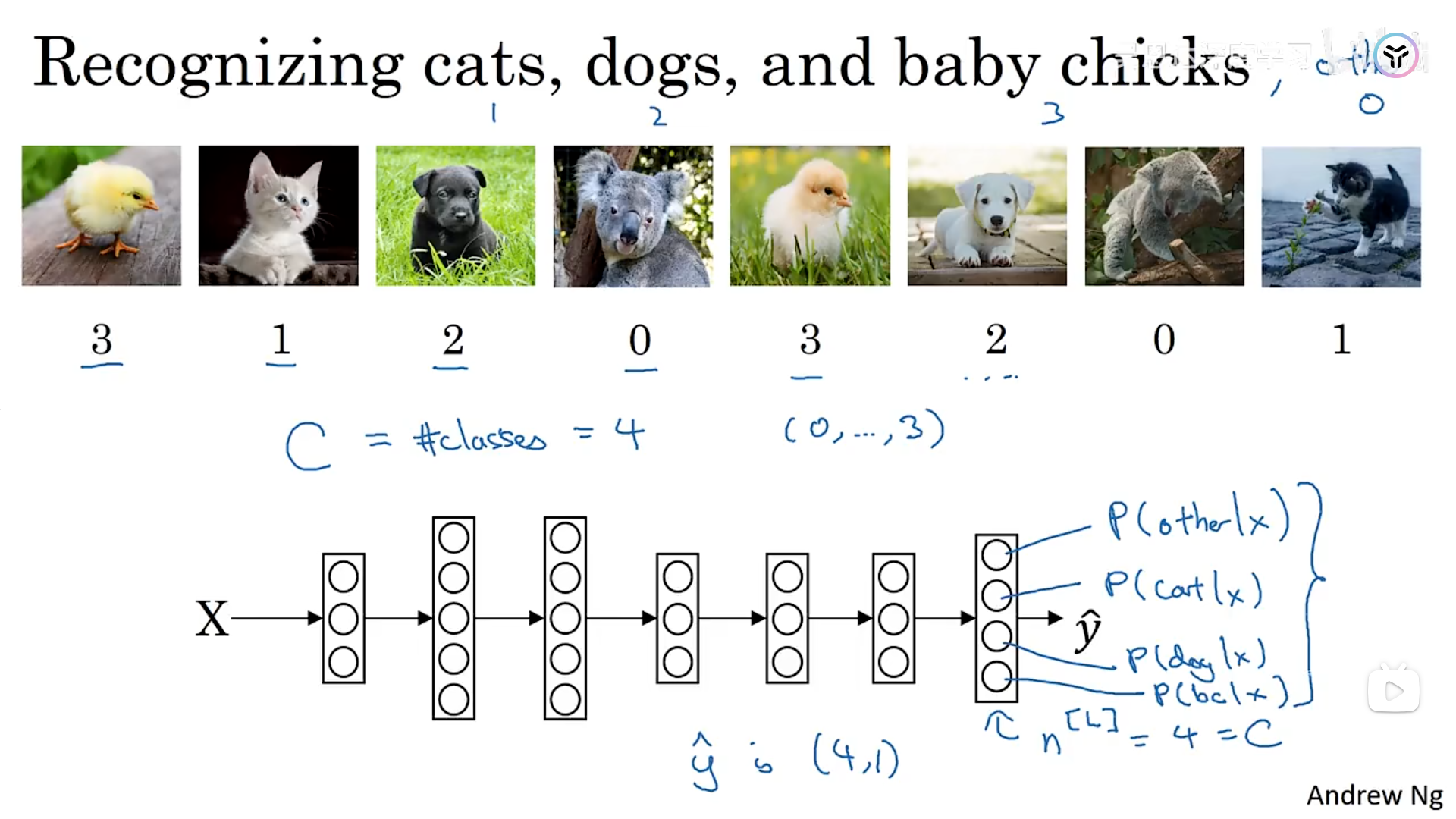
为了实现这个算法，我们应该使用输出层中的softmax，具体实现如下。

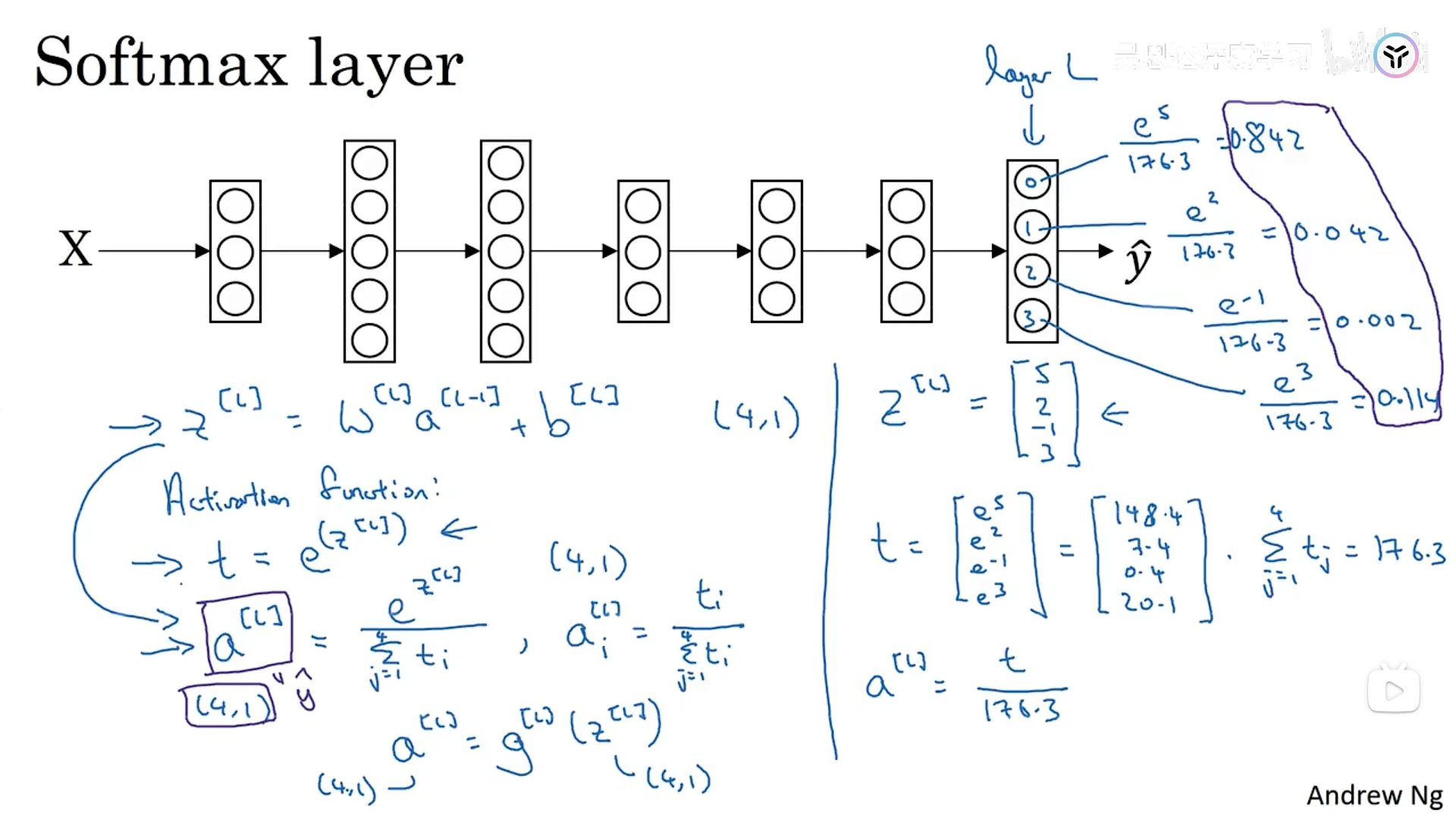
softmax的计算方法图中已经标明了，重点就是其中我们需要对z求指数次方，然后进行归一化，计算出来的值就代表这个数据属于某个类别的概率，和为1。

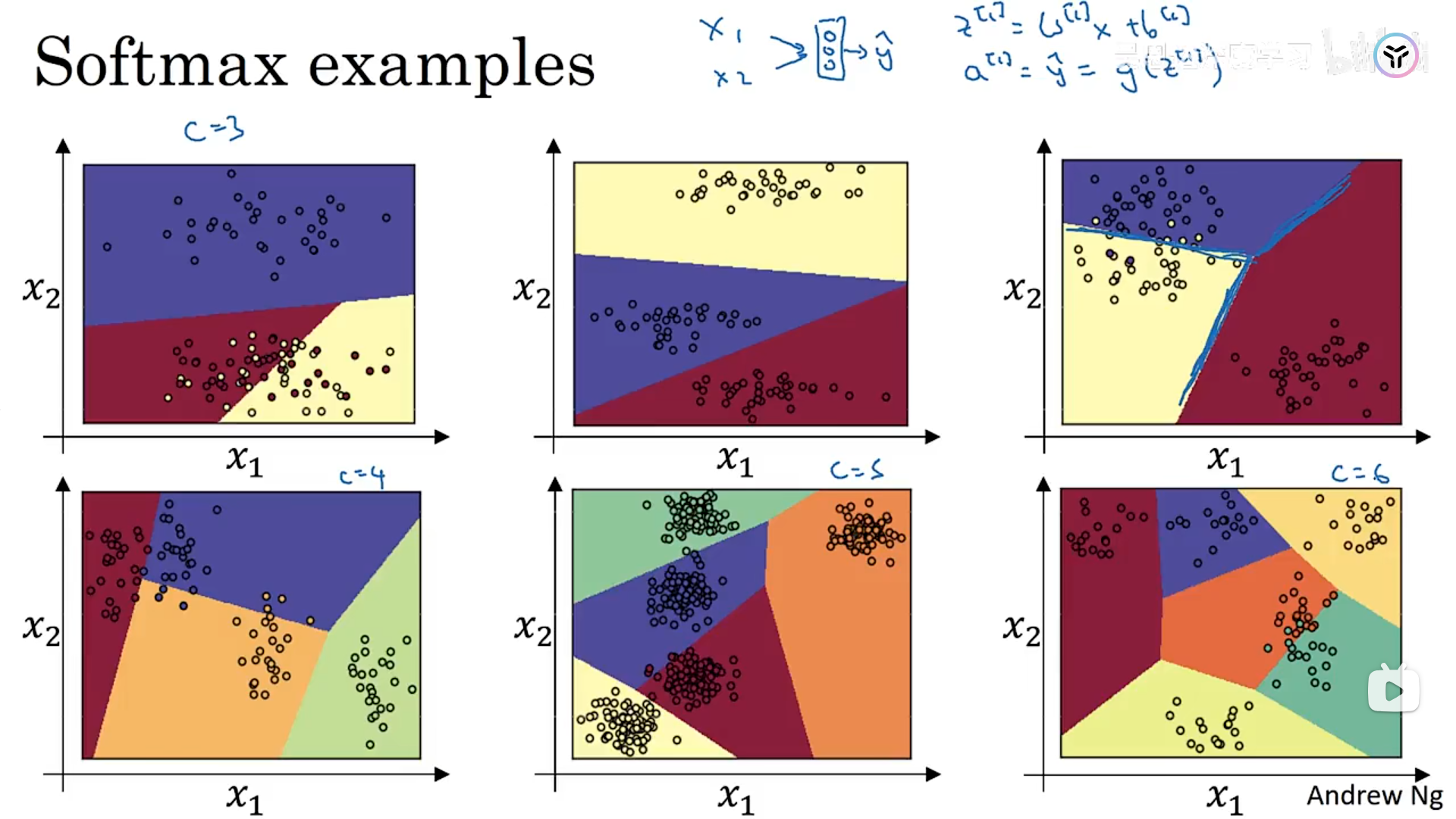
接下来是一些具体的应用示例：softmax分类器可以计算出决策边界，这是没有隐藏层的softmax，线性决策边界；当然使用深度神经网络，输出层用softmax，可以学习到更加复杂的决策边界。

3.2 训练一个softmax分类器

当我们将逻辑回归的输出类别数设置为2的话，实质上就是逻辑回归。

下面展示了softmax的损失函数和成本函数，其中预测值为0或者1是我们在模型输出时，将概率最大值输出为1，其他的输出为0，成本函数和损失函数的计算方式直接看ppt就能看懂。

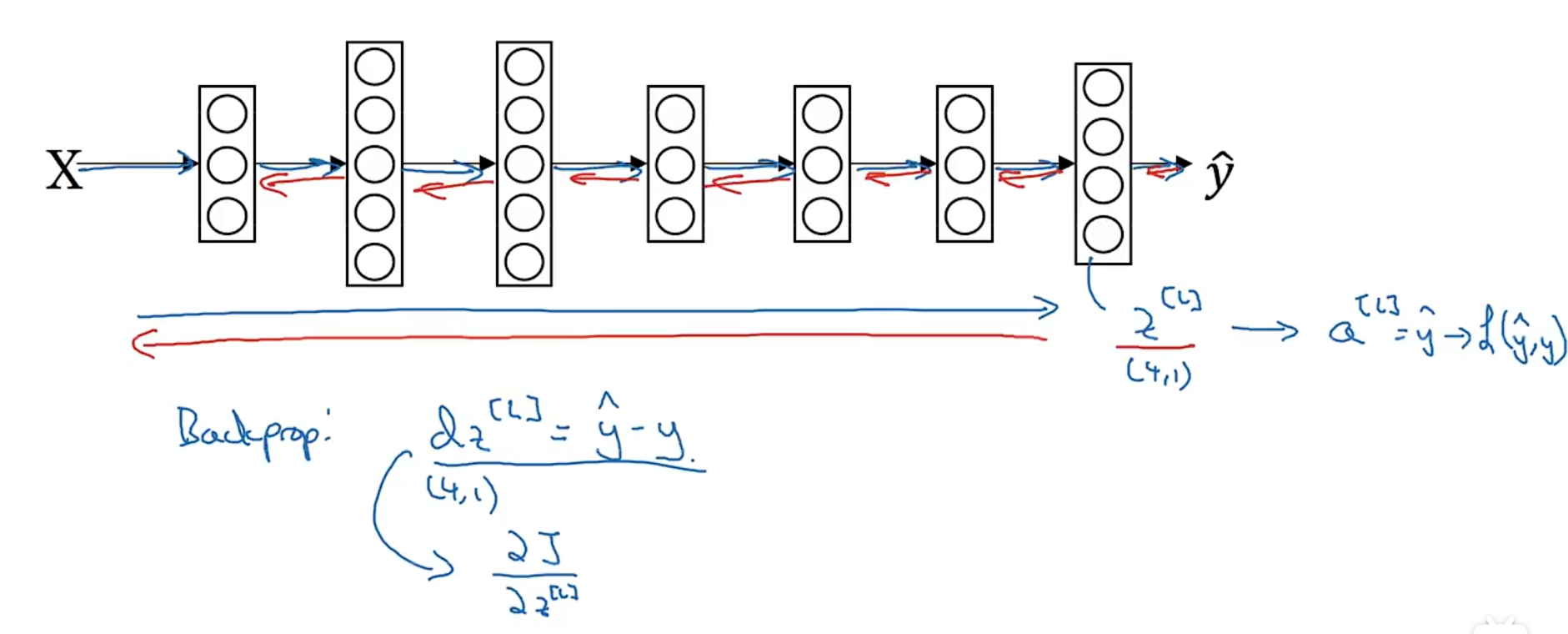
那当我们训练一个输出层为softmax激活函数的深度神经网络是，最后一层的反向传播应该如何做（图示）。

四、一些深度学习框架

选择深度学习框架的一些建议：编程容易、运行速度、真正开放、编程的语言。

五、tensorflow深度学习框架

下面是一个应用tensorflow框架的一个示例：在设置成本函数时，框架会构建一个成本函数的计算图，并内置了所有必要的逆函数，方便我们后续进行反向传播，因此无需显式实现反向传播。

5.1 介绍一些tensorflow框架会使用到的一些个函数

这里解释其中几个重要库的功能：math进行数学运算、numpy进行矩阵/张量运算、matplotlib进行图形绘制、tensorflow是深度学习库、ops是计算图。tf.constant(值，name=“常量名”)用于定义常量，tf.variable(变量初始值，name=“变量名”)用于定义变量，tf.multiply(a,b)计算ab的乘积。

x = tf.placeholder(tf.int64, name = ‘x’)

print(sess.run(2 * x, feed_dict = {x: 3}))，定义一个变量的占位符并传入值。

由于源代码给的是tensoflow1.x版本，版本太低，且只支持3.6/3.7python版本，因此我只截取了部分函数代码。