基本算法—d.三分法（Ternary Search）

三分法（Ternary Method）（数学应用、决策应用、社会应用、三分类）

三分法（Ternary Method），在不同的领域有不同的应用，主要指的是在某些情况下将问题或过程分成三部分进行处理。这里，我将从几个常见的角度介绍三分法，包括数学、算法和决策中的应用。

一、三分法在数学中的应用

在数学中，三分法通常指的是将一个区间分成三个部分，进行迭代计算的过程。最常见的应用是三分查找（Ternary Search），它是优化问题中寻找最优解的一种方法。

1. 三分查找法（Ternary Search）

三分查找是一种用于求解单峰函数最小值或最大值的优化算法，尤其适用于区间上的优化问题。其思想与二分查找相似，但每次将区间分为三个部分，而不是两个。三分查找能在每次迭代中缩小搜索范围的大小，从而加速寻找最优解的过程。

原理：

• 给定一个函数 f(x)，我们希望找到 f(x) 的最小值或者最大值。
• 假设目标函数是单峰的，即存在一个局部最小点或者最大点。
• 在每次迭代中，将区间 [low, high] 分成三部分，比较三个点的函数值，根据比较结果选择一个最优的区间进行递归。

步骤：

1. 将区间 [low, high] 分成三等分，分别为 x1 = low + (high - low) / 3 和 x2 = high - (high - low) / 3。
2. 计算 f(x1) 和 f(x2)。
3. 根据 f(x1) 和 f(x2) 的大小关系，判断最小值或最大值所在的区间。
4. 继续在选定的子区间进行搜索，直到区间足够小为止。

优缺点：

• 优点：比起二分查找，三分查找在某些问题上可能更有效，尤其是在目标函数是单峰的情况下。
• 缺点：三分查找相对而言计算开销稍大，因为每次计算时需要两个值而非一个。

示例：

假设我们有一个函数 f(x) = -(x - 2)^2 + 4，我们希望找到该函数的最大值。通过三分查找可以通过以下步骤逼近最值。

二、三分法在决策中的应用

三分法还常被应用于决策分析中，尤其是在有多个选择或可能结果的情况下，常用于将问题或任务分解为三部分或三种选择，并通过权衡分析做出决策。经典的例子包括：

1. 三分法决策模型

在决策分析中，三分法是一种用于判断问题或任务如何分配或进行决策的模型。它通常在面对三个主要选择时使用，比如：

• 第一种选择：一个方案或决定。
• 第二种选择：一个替代方案。
• 第三种选择：不做决定或选择一个完全不同的方案。

三分法在这种背景下通常通过以下方式运作：

• 对每种选择进行分析。
• 比较每种选择的优劣。
• 最终基于某些标准（如成本、效益、风险等）做出最适合的决策。

三、三分法在政治或社会决策中的应用

在一些复杂的社会和政治决策过程中，三分法也有应用。它常常涉及将复杂的决策问题分为三部分，以便不同的利益相关者或决策者可以分别对这三部分进行评估或投票，从而最终达成共识。这里的三分法可以帮助减少决策的复杂度，促使更具效率的解决方案。

四、三分法与三分类法（Ternary Classification）

在机器学习和数据科学中，三分法还可以指代三分类问题（Ternary Classification）。在这种情况下，目标是将数据点分类为三种不同的类别。

应用场景：

• 图像分类：将图像分为三种类型，如“猫”，“狗”，“鸟”。
• 情感分析：对文本进行情感分析，可能会将情感分为三类，如“正面”，“中性”，“负面”。
• 医学诊断：将病人分类为三种情况，如“健康”，“轻微疾病”，“严重疾病”。

# 1.原理 三分法常用于求单峰（或者单谷）的极值，是二分法的一个简单扩展。

三分法原理

• 给定一个函数 f(x)，我们希望找到 f(x) 的最小值或者最大值。
• 假设目标函数是单峰（单谷）的，即存在一个局部最小点或者最大点。
• 在每次迭代中，将区间 [low, high] 分成三部分，比较三个点的函数值，根据比较结果选择一个最优的区间进行递归。
• 最后将区间收敛缩小到可接受的范围，使用$ \frac{(low+high)} 2 $作为近似解

为什么不通过求导函数的零点来求极值点？

客观上，求出导数后，通过二分法求出导数的零点（由于函数是单峰函数，其导数在同一范围内的零点是唯一的）得到单峰函数的极值点是可行的。

但首先，对于一些函数，求导的过程和结果比较复杂。

其次，某些题中需要求极值点的单峰函数并非一个单独的函数，而是多个函数进行特殊运算得到的函数（如求多个单调性不完全相同的一次函数的最小值的最大值）。此时函数的导函数可能是分段函数，且在函数某些点上可能不可导。

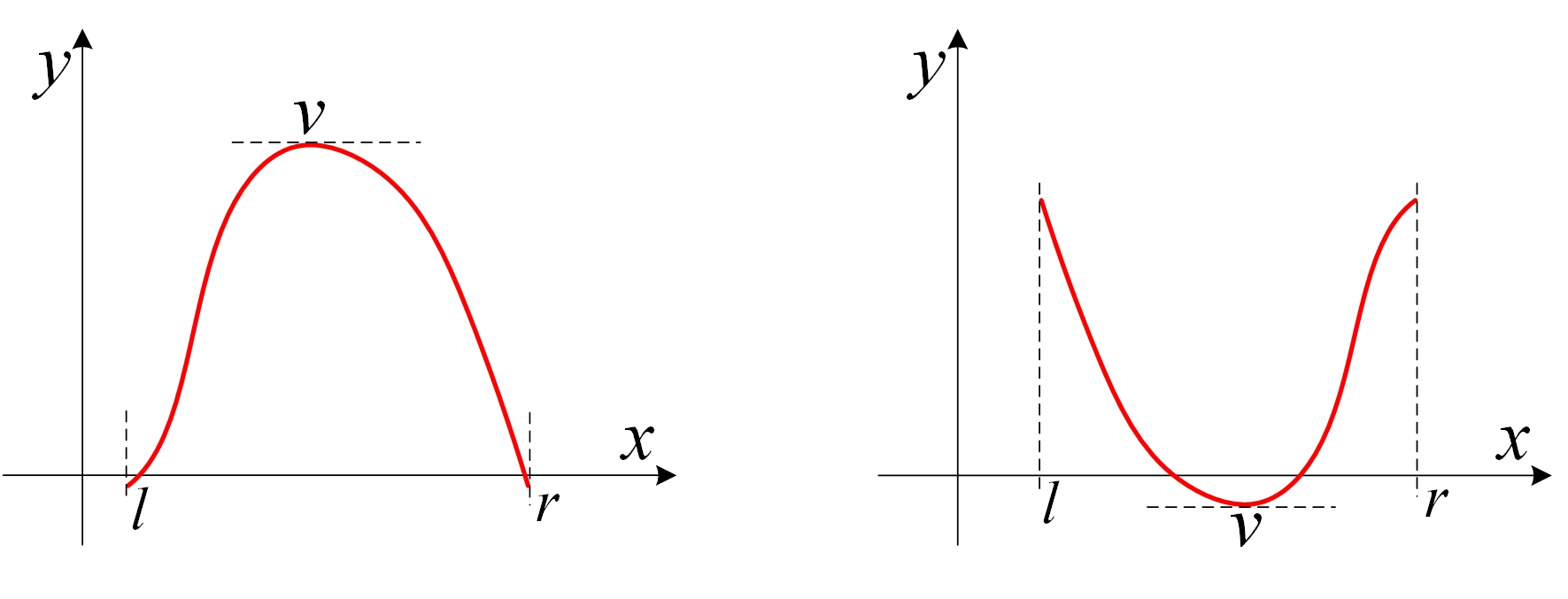
单峰函数和单谷函数

单峰函数 （左） 和单谷函数如下图，

1. 函数f(x)在区间[l, r]内，只有一个极值v，
2. 在极值点两边，函数是严格单调变化的。

以单峰函数为例，在v的左边，函数是严格单调递增的，在v右边是严格单调递减的。

区间迭代原理

虽然不能直接用二分法，不过，只要稍微变形一下，就能用了。

在[l, r]上任取2个点，mid1和mid2，把函数分成三段。有以下情况：

（1）若f(mid1) < f(mid2)，极值点v一定在mid1的右侧。此时，mid1和mid2要么都在v的左侧，要么分别在v的两侧。如下图所示。

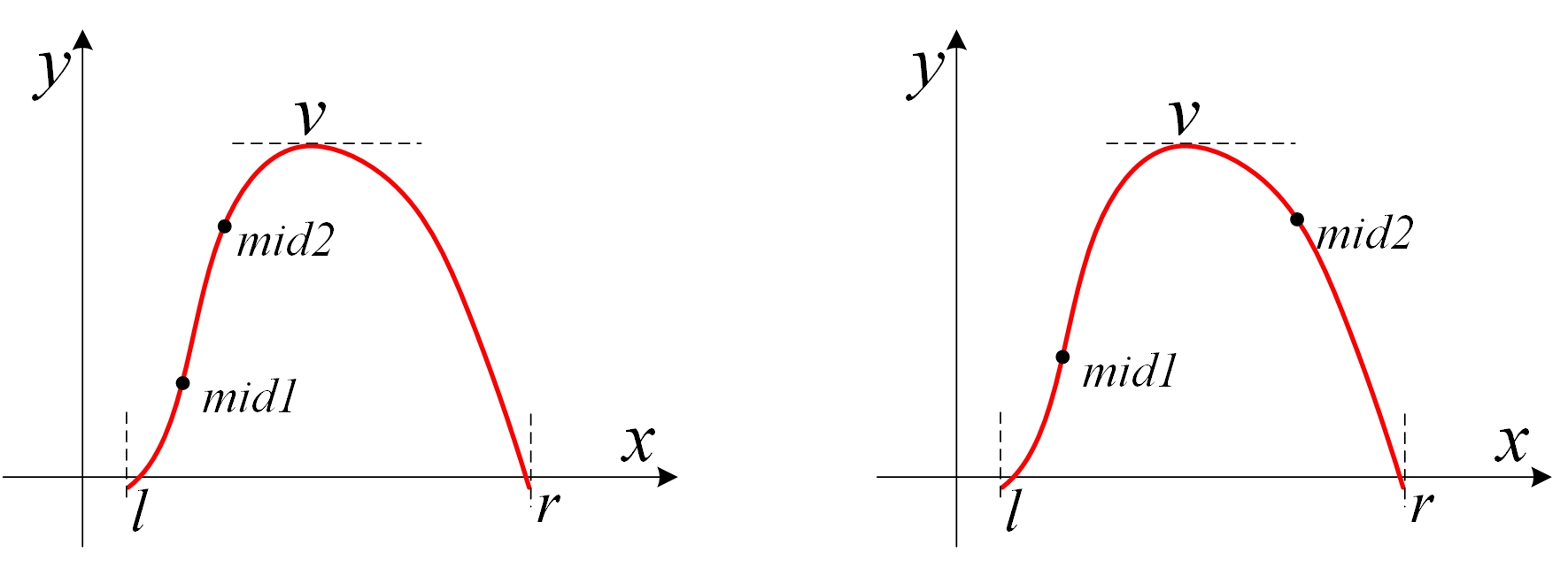
下一步，令l = mid1，区间从[l, r]缩小为[mid1, r]，然后再继续把它分成三段。

（2）同理，若f(mid1) > f(mid2)，极值点v一定在mid2的左侧。如下图所示。下一步，令 r = mid2，区间从[l, r]缩小为[l, mid2]。

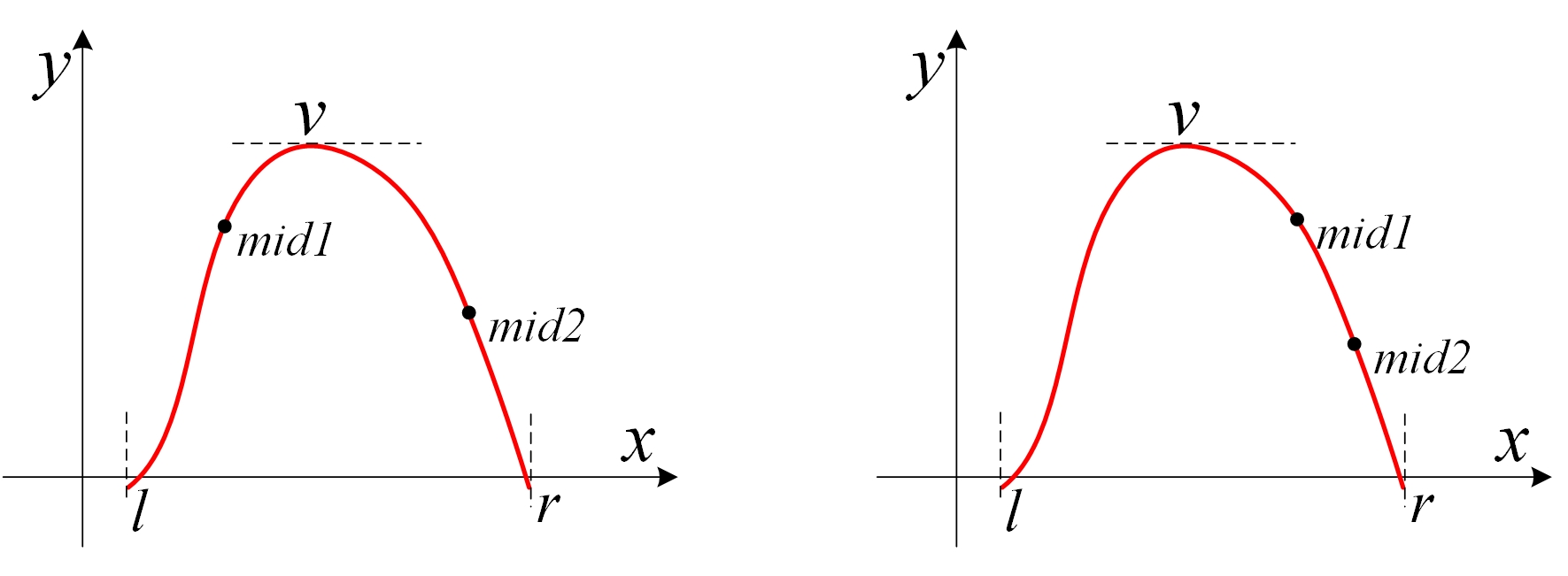
不断缩小区间，就能使得区间[l, r]不断逼近v，从而得到近似值。

mid1 和 mid2 的取法

（1）三等分：mid1和mid2为[l, r]的三等分点。那么区间每次可以减少三分之一。

（2）近似三等分（类似二分）：计算[l, r]中间点mid = (l + r) / 2，然让mid1和mid2非常接近mid，例如mid1 = mid - eps，mid2 = mid + eps，其中eps是一个很小的值。那么区间每次可以减少接近一半。

2.实数三分（原理同上）

3.整数三分（原理同上）

点击——快捷跳转到 codeforce 对应知识点题目