前言
微分方程是包含 连续变化的自变量、 未知函数及其 变化率的方程式。
当我们的研究对象涉及某个过程或物体随时间连续变化的规律时，通常会建立微分方程模型。
美赛的A题（连续型），用连续函数建立一类模型。常用方法就是微分方程，并多为“数值分析”领域的内容，需要熟练掌握偏微分方程建模能力。
本文正文第一部分关注捕鱼业的持续收获问题，从 logistics 方程入手分析产量，再具体深入，研究捕捞效益和过度捕捞的问题。
第二部分关注资金、劳动力与经济增长的问题，但本文不做深入，仅点到 Douglas生产函数为止。
一、捕鱼业的持续收获
本节要建立在捕捞情况下渔场遵从的方程，分析鱼量稳定的条件，并且在稳定的前提下讨论如何控制捕捞使持续产量或经济效益达到最大，最后研究捕捞过度的问题。
1.产量模型
记时刻 t 渔场中鱼量为 x( t )，关于 x( t )的自然增长和人工捕捞作如下假设：
- 在无捕捞条件下 x( t )的增长服从logistics 方程；
- 单位时间内捕捞量与渔场鱼量 x( t )成正比，比例常数 E 表示单位时间捕捞率，又称为捕捞强度，可以用捕鱼网眼大小或出海渔船数量来控制强度。
由假设1， 用 f( x )表示单位时间的增长量
由假设2，用 h( x )表示单位时间的捕捞量
得到
我们并不用解方程得到 x( t )的动态变化过程，只希望知道渔场的稳定鱼量和保持稳定的条件
令
得到两个平衡点
不难算出
所以，当捕捞适度（E < r），就可使渔场鱼量稳定在 
从而获得持续产量E。
进一步讨论渔场鱼量稳定在的前提下，如何控制捕捞强度E，使持续产量最大化
此时有
由 f( x )性质不难得到，当=N /2时，有最大产量 hm = rN /4，此时 E = r /2
2.效益模型
从经济角度看，不应追求产量最大，而应考虑效益最佳。
不妨简单假设：鱼的销售单价为常数 p，单位捕捞率的费用为常熟 c，那么单位时间的收入 T 和 支出 S 分别为
单位时间利润为
在稳定条件下代入得
不难得到，当利润最大时，捕捞强度为
3.捕捞过度
上面的效益模型是以计划捕捞为基础的。当渔场向众多盲目的经营者开放，比如在公海上无规则的捕捞，这种情况称为盲目捕捞，将导致捕捞过度
（1）式给出了利润与捕捞强度的关系，令 R = 0解为E1
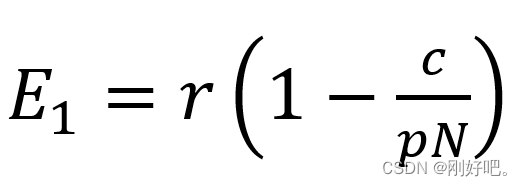
当E < E1,利润大于0，盲目的经营者会加大捕捞强度；若E > E1,利润小于0，他们当然要减小强度，所以E1 为盲目捕捞的临界强度。
将E1 代入可得，此时渔场稳定鱼量为 x1 = c / p，即鱼量完全由成本—价格比决定。
二.资金、劳动力与经济增长
本节的模型将首先建立产值与资金、劳动力之间的关系，然后研究资金与劳动力的最佳分配，使投资效益最大，最后讨论如何调节资金与劳动力的增长率，使劳动生产率得到有效的增长。
1.Douglas生产函数
用 Q( t )，K( t )，L( t )分别表示某一地区或部门在时刻 t 的产值、资金和劳动力，它们的关系一般记作
Q( t )=F( K( t )，L( t ) ) (1)
其中F为待定函数，对于固定的时刻 t ，上述关系写作
Q =F( K , L) (2)
为寻求F的函数形式，引入记号
z = Q / L，y = K/ L (3）
其中z 是每个劳动力的产值，y 是每个劳动力的投资。如下的假设是合理的：z 随着 y 的增加而增长，但增长速度递减。进而简化地表示为
z = c g(y)，g(y) = ，0<a<1 （4）
常数 c >0 可以看成技术的作用。由（3）,（4）可得（2）中 F 的具体形式为
Q=c ，0<a<1 （5）
由（5）易知，Q 有如下性质
，
，
,
（6）
即满足产值Q 随资金 K 和劳动力L 的增加而增长，但增长速度递减，且a 的大小反映了资金、劳动力对创造产值的轻重关系。
（5）式就是经济学中著名的 Douglas生产函数，它经受了资本主义社会的检验，更一般的形式为
Q=c，0<a,b<1 （7）
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
