【数学建模】微分方程（一）

前言

微分方程是包含 连续变化的自变量、 未知函数及其 变化率的方程式。
当我们的研究对象涉及某个过程或物体随时间连续变化的规律时，通常会建立微分方程模型。

美赛的A题（连续型），用连续函数建立一类模型。常用方法就是微分方程，并多为“数值分析”领域的内容，需要熟练掌握偏微分方程以及精通将连续性方程离散化求解的编程能力。

本文正文中的第一部分人口增长问题，重点介绍logistics模型，它就可以在2019年美赛A题中的科学养龙中，描述随着年龄增长龙的体重变化。

第二部分药物中毒急救，以简单的实例，让读者了解微分方程的建模过程。

---

一、人口增长

1. 指数增长模型

1789 年，Malthus 提出了 Malthus 人口模型，又称为 指数增长模型模型。

假设如下：

1. 将人口看作连续时间 t 的连续可微函数 x( t )

2. 单位时间人口的增长率 r 是常数（增长率=出生率—死亡率）

3. rx( t )就是单位时间内 x( t )的增量

然而，指数增长模型计算结果与实际数据相差很大，主要原因是增长率 r 并非常数。

2. logistics模型

在分析人口增长到一定数量后增长率下降的主要原因时，人们注意到，自然资源、环境条件等因素对人口增长起着阻滞作用，并且随着人口的增加，阻滞作用越来越大，由此提出logistics模型，又称阻滞增长模型。

假设如下：

1. 阻滞作用体现在对人口增长率 r的影响上,使得 r 随着人口数 x的增加而下降。

2. 自然资源和环境条件所能容纳的最大人口数据 Xm，称人口容量。当 x=Xm 时人口不再增长，即此时增长率为0。

由此导出

结合指数增长模型得

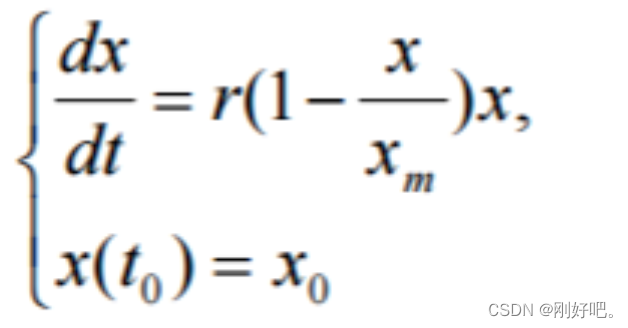
解得

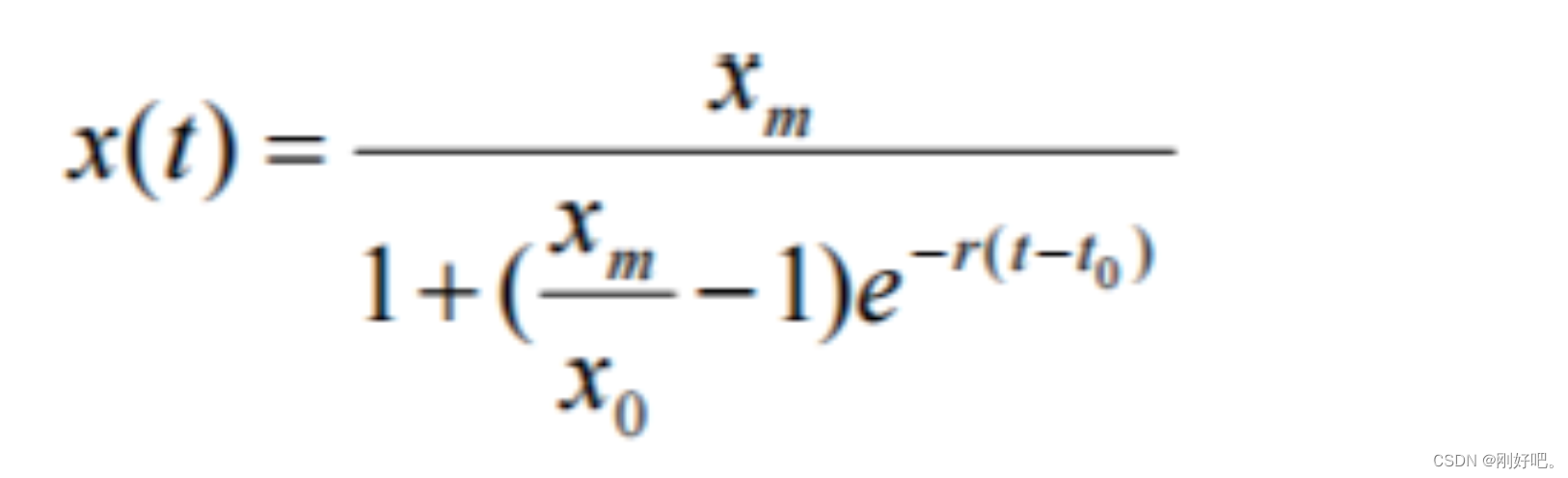
函数如图

---

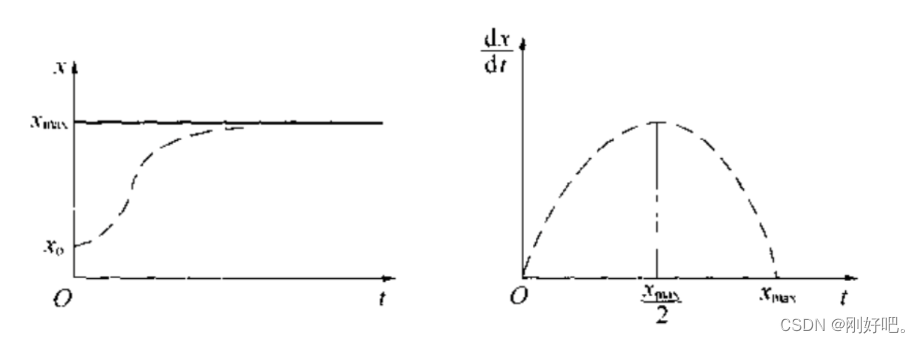
二、药物中毒急救

1.背景

两小时前，一小孩误服1100 mg 某药物，血药浓度达到0.1 mg/ml 时会严重中毒，达到0.2 mg/ml 时会致死。从药物说明书可知，该药物的吸收的半衰期约 5h，排除的半衰期约 6h。试计算此时的血药浓度。

2.假设

1. 孩子的血液总量为2000 ml

2. 该药物的吸收的半衰期为 5h，排除的半衰期为 6h

3. 肠胃道中药物向血液系统的转移率和药量 x( t ) 成正比，比例系数记作 m，总剂量1100 mg 的药物在 t = 0 瞬间进入肠胃道

4. 血液系统中药物的排除率与药量 y( t ) 成正比， 比例系数记作 n，t = 0 时血液中无药物

3.建模

由假设3 得

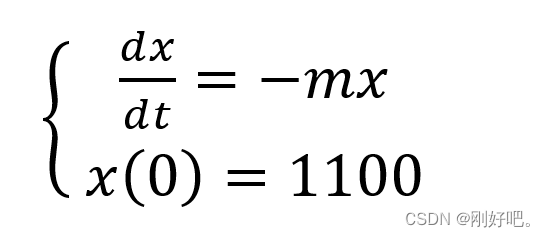
由假设4 得

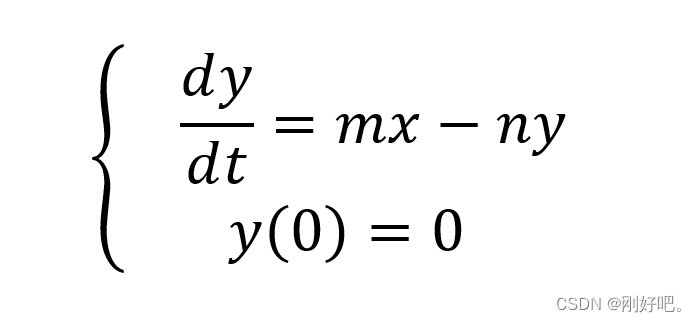
解得

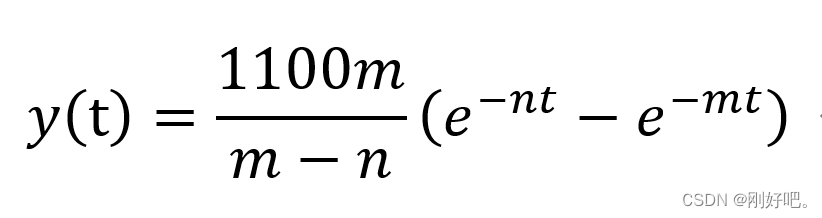
由药物吸收的半衰期和排除的半衰期可以确定m，n