西瓜书学习第三章学习笔记

3.1一元线性回归

例题引入  通过身高预测体重

收集到的一批样本数据并通过坐标轴表示，通过数据模型会发现一条于数据拟合的数学函数线。线性回归就是求得到的模型在x处获得的数据f（x）与样本数据y在平行Y轴上的误差并且使之最小，误差可以通过计算均方误差来进行比较，既

w（x,b）=Σ（yi-f（x））² 

给定由d个属性描述的示例x=(x1;x2;...;xa); 其中xi是x在第 i个属
性上的取值，线性模型(linear model)试图学得一个通过属性的线性组合来进行
预测的函数，即

                    f(x)=W1x1+w2x2+..+wxd+b,一般用向量形式写成
                    f(x)=wx+b,
其中w=(W1;w2;...;wa).w和b 学得之后，模型就得以确定。

下面是常用的模型（假设空间):

1.仅通过身高预测体重

f（x）=W1X1+b，,认为身高是连续的，所以给他一个权重W1

2.二值离散特征（颜值）（好看为1，不好看为0）

f(x)=W1X1+W2X2+b

3.有序的多值离散型特征（饭量）这种数值存在一种叫做序的关系，饭量大的叫做1，饭量小的叫0。

f(x)=W1X1+W2X2+W3X3+b

4.无序的多值离散型特征（肤色）（黄[1,0,0] 黑[0,1,0] 白[0,0,1])每个数据都有着相同的地位与权重，相当于把每个数据拆成二值特征

f(x)=W1X2+W2X2+W3X3+W4X4+W5X5+W6X6+b

3.1.2最小二乘估计
基于均方误差最小化来进行模型求解的方法称为最小二乘法

E（x,b）=Σ（yi-f（x））² =Σ（yi-（WXi+b））² =Σ（yi-WXi-b）² 

此时平行距离最小时为所求结果

3.1.3极大似然估计

用途：估计概率分布的参数值
方法：对于离散型(连续型)随机变量X，假设其概率质量函数为P(x；θ)(概率密度函数为p(x；θ)，其中θ为待估计的参数值(可以有多个)。现有X1，X2，X3，Xn是来自X的n个独立同分布的样本，它们的联合概率为
L(θ)=Π P(xi；θ)
其中X1，X2，X3，.，Xn是已知量，是未知量，因此以上概率是一个关于的函数，称L(0)为样本的似然函数。极大似然估计的直观想法：使得观测样本出现概率最大的分布就是待求分布，也即使得联合概率（似然函数）L(0)取到最大值的θ*即为θ的估计值。

例现有一批等待观测的样X1,X2,X3..Xn，假设其服从正态分布X～（μ，σ²），其中μ σ未知，请用极大似然估计求值。

1.第一步，写出随机变量X的概率分布函数

p（x；μ，σ²）=1/√2πσexp（-（x-μ）²/2σ²）

2.写出似然函数

L(μ,σ²)=Πp(xi;μ,σ²)=Π1/√2πσexp(-(xi-μ)²/2σ²

3.求出使得L（μ，σ²）取到最大值得μ，σ

对于线性回归来说，也可以其为一下模型

y=wx+b-ε

其中ε是不受控制的误差，通常假设为其服从均值为0的正态分布

所以ε的概率密度函数为

1/√2π σexp(-ε²/2σ²)

可利用y-wx-n替换ε 得到

L(μ,σ²)=Π1/√2πσexp（(-y-wx-b)²/2σ²）

=Σln1/√2πσ+Σlnexp（(-y-wx-b)²/2σ²）

=mln1/√2πσ-1/2σ²Σ(y-wx-b)²

其中，μσ是常数，所以最大化L（）就是最小化Σ(y-wx-b)²，等价于最小二乘估计。即为损失函数。 

3.1.3求解在损失函数最小时的对应的w和b

1.证明E（w，b）是一个凸出集

定理设D∈R∧n是非空凸出集f：D∈R∧n->R,并f（小）在D上二阶连续可微，如果f（小）的海塞矩阵在D上是半正定的，则f（x）是D上的凸函数。因此，只需要证明E(w,b)=Σ（yi-wxi-b）的海塞矩阵是半正定的。

Δ²E（w，b）=[δ²E(w,b)/δγ²       δ²E(w,b)/δbγ  ]                                         

                       [ δ²E(w,b)/δγb       δ²E(w,b)/δ ²  ]

经过二阶求导所得到的矩阵为

Δ²E（w，b）=[2ΣXi² 2ΣXi]

                       [2ΣXi  2m ]

半正定的矩阵的判定定理是若实对称矩阵的所有顺序子式均是非负的，该矩阵半正定。

Δ²E（w，b）=[2ΣXi² 2ΣXi]

                       [2ΣXi  2m ]=4mΣxi²-4（Σxi）²

可得次矩阵大于0，E（w，b）是一个凸函数

2.根据凸函数性质求w，b。

凸函数充分性定理：若f是凸函数，并且f一阶连续可微，则x*是全局的必要条件是ΔE（x* ）=0。

ΔE（w，b）=0的点也是最小值点。即

ΔE（w，b）=[δE(w,b)/δw]=[0]

                     [δE(w,b)/δb]   [0]

根据两个一阶导数列出方程组即可求解w，b。

小结

机器学习三要素

 

1.模型：根据具体问题，确定假设空间。

2.策略：根据评价标准，确定最优模型的策略（通常会产出一个损失函数）

3.算法：求解损失函数，确定最优模型。

3.2多元线性回归

更一般的情况下，类似开头提到的含有多个属性的情况即

f(x)=W1x1+w2x2+..+wxd+b,一般用向量形式写成。

与一元线性回归一样，也需要通过求的最小的损失函数来确定w与b。

为此我们可以将f（x）的b改写，写成

f(x)=W1x1+w2x2+..+WdXd+W(d+1)*1

w∧=(W1,W2..,W（d+1) )

x∧=(X1,X2..,1)

因此f（x）可以写成f（x∧）=w∧*x∧（两个向量内积的形式）

又最小二乘法

Ew=Σ（yi-f（x∧））²=Σ（yi-w∧x∧）² 

线。 

      与前面一元线性回归推导过程类似，不再具体推导。

       此时要拟合的曲线可能受多个因素影响。       

f（x）=W1X1+W2X2+...+WdXd+b

前面提到的 X 就变为西瓜书中所示： 

x=[x11  x12 ..x1d]     [X1t   1]

   [x21  x22..x2d]  = [X2t    1]

   .        .           .       .       .

  [xm1 xm2..xmd]    [x3t  1]

      求解W仍然是：

W=(XtX)∧-1XY

3.3.1 单位跃迁函数与对数几率函数

分类任务也可以作为线性模型的推广，以二分类为例，对z=wTae+b，我们需要把z转化

为0/1值，那么理想的转化是这样的

               {    0， z<0;

    f(x)=   {  0.5, z = 0;

               {   1， z ＞ 0;

这就是“单位跃阶函数”。但它的缺陷是不连续，所以没法直接用作广义线性模型中的

g1（·）为此我们选择了一个能近似单位跃阶函数的替代函数，这里我们选择了对数几率函数

y = 1/1+e∧-2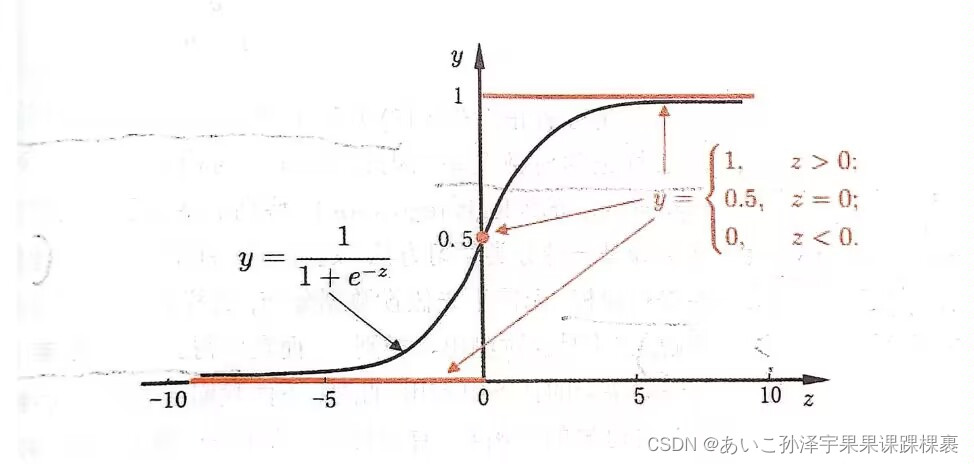

 

将对数几率函数作为g-1(·)建立广义的线性模型

y= 1/1+exp(wTx+b)

可化为

ln(y/1-y) =wTx+b

如果把y视为样本c作为正例的可能性，则1-y是其反例的可能性，两者的比值

称为几率，反映了x作为正例的相对可能性，对几率取对数，就称为“对数几率”

1n(y/1-y)

所以说对数几率模型的本质是用线性回归的预测结果去逼近真实标记的对数几率。这种方法的优点如下：

1.直接对分类可能性进行建模，无需事先假设数据分布，避免了假设分布不准确的问题；

2.不仅预测出“类别”，而是得到近似概率预测，对概率辅助决策的任务很有用；

3.对数回归模型需要求解的目标函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解。