[蓝桥杯 2023 省 A] 更小的数--题解

题目链接在这里：

[蓝桥杯 2023 省 A] 更小的数 - 洛谷

# [蓝桥杯 2023 省 A] 更小的数

## 题目描述


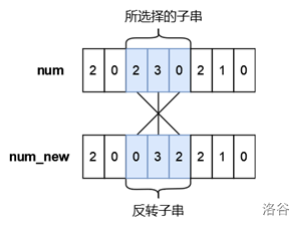
小蓝有一个长度均为 $n$ 且仅由数字字符 $0 \sim 9$ 组成的字符串，下标从 $0$ 到 $n-1$，你可以将其视作是一个具有 $n$ 位的十进制数字 $num$，小蓝可以从 $num$ 中选出一段连续的子串并将子串进行反转，最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 $num_{new}$ 满足条件 $num_{new}<num$，请你帮他计算下一共有多少种不同的子串选择方案，只要两个子串在 $num$ 中的位置不完全相同我们就视作是不同的方案。

注意，我们允许前导零的存在，即数字的最高位可以是 $0$，这是合法的。

## 输入格式

输入一行包含一个长度为 $n$ 的字符串表示 $num$（仅包含数字字符 $0 \sim 9$），从左至右下标依次为 $0 \sim n-1$。

## 输出格式

输出一行包含一个整数表示答案。

## 样例 #1

### 样例输入 #1

```
210102
```

### 样例输出 #1

```
8
```

## 提示

#### 【样例说明】

一共有 $8$ 种不同的方案：

1. 所选择的子串下标为 $0\sim1$，反转后的 $num_{new} = 120102 < 210102$；
2. 所选择的子串下标为 $0\sim2$，反转后的 $num_{new} =  012102 < 210102$；
3. 所选择的子串下标为 $0\sim3$，反转后的 $num_{new} =  101202 < 210102$；
4. 所选择的子串下标为 $0\sim4$，反转后的 $num_{new} =  010122 < 210102$；
5. 所选择的子串下标为 $0\sim5$，反转后的 $num_{new} =  201012 < 210102$；
6. 所选择的子串下标为 $1\sim2$，反转后的 $num_{new} =  201102 < 210102$；
7. 所选择的子串下标为 $1\sim4$，反转后的 $num_{new} =  201012 < 210102$；
8. 所选择的子串下标为 $3\sim4$，反转后的 $num_{new} =  210012 < 210102$。

#### 【评测用例规模与约定】

对于 $20\%$ 的评测用例，$1 \le n \le 100$；

对于 $40\%$ 的评测用例，$1 \le n \le 1000$；

对于所有评测用例，$1 \le n \le 5000$。

题解：

这道题虽然说是找到更小的数，其实就是在这个字符串里找到一对数num[i]和num[j]（i<j），保证num[i]>num[j]，这样交换之后肯定能保证交换后的数一定比原来小（这里题干给的前导零允许存在就大大降低了难度），如果num[i]<num[j]，那么交换之后肯定不会比原来小，那么就只剩下一种情况：num[i]==num[j]，这时候就要判断num[i+1]和num[j-1]的大小，如此循环往复，直到分出大小，然后再根据上面的情况进行判断， 因为有一直相等的情况，所以循环条件也有tempi<tempj这一限制，最后附上代码：

代码：

#include <bits/stdc++.h>
using namespace std;
#define N 100010
#define ll long long
int main()
{
    string s;
    cin >> s;
    ll res = 0;
    int len = s.size();
    for (int i = 0; i < len; ++i)
    {
        for (int j = i + 1; j < len; ++j)
        {
            if (s[i] > s[j])
            {
                res++;
            }
            else if (s[i] == s[j])
            {
                int tempi = i, tempj = j;
                while (tempi < tempj && s[tempi] == s[tempj])
                {
                    tempi++;
                    tempj--;
                }
                if (s[tempi] > s[tempj])
                {
                    res++;
                }
            }
        }
    }
    cout << res;
    return 0;
}