【算法】一篇文章弄清楚KMP算法的实现

目录

 

前言：

        一.KMP算法简介：

        二.next数组的介绍及实现

        三.next数组的优化

        四.伪代码和完整代码的实现

总结：        

---

博客主页：张栩睿的博客主页

欢迎关注：点赞+收藏+留言

系列专栏：c语言学习

        家人们写博客真的很花时间的，你们的点赞和关注对我真的很重要，希望各位路过的朋友们能多多点赞并关注我，我会随时互关的，欢迎你们的私信提问，也期待你们的转发！

        希望大家关注我，你们将会看到更多精彩的内容！！！

前言：

        我们都知道，BF算法，就是用两层循环来实现，外层循环用一个循环变量 i 遍历主字符串str1，每当在主字符串中找到子字符串的首元素就进入第二层循环进行两个字符串的匹配，若匹配失败，指针 i 回溯到匹配的起始位置继续寻找下一个子字符串首字符，同时 j 指针也回到子字符串的首地址，重复上述步骤。

        而KMP 算法是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 三位神人共同提出的，称之为 Knuth-Morria-Pratt 算法，简称 KMP 算法。该算法相对于 Brute-Force（暴力）算法有比较大的改进，主要是消除了主串指针的回溯，从而使算法效率有了某种程度的提高。那么，KMP是如何提高算法效率的呢？

   一.KMP算法简介：

        上面说道 KMP 算法主要是通过消除主串指针的回溯来提高匹配的效率的，那么，它是则呢样来消除回溯的呢？就是因为它提取并运用了加速匹配的信息！
        KMP算法在主串和模式串匹配失败时，会利用匹配过程中已经成功匹配的部分字符的相关信息(字符串最大相等前后缀长度)，让维护模式串的指针回退到合适的位置而维护主串的指针不进行回退操作，继续向后匹配。kmp算法中维护主串的指针只递增不回退，从而使查找的时间复杂度降为线性复杂度。

        这里我们就不得不引出一个数组：Next数组。这是一个神奇的数组，也是KMP算法最难弄懂的代码。只要弄懂了 next 的求解方法，也就弄懂了 KMP 算法的十之七八了。

对于BF比较，我们逐个比较，时间复杂度大，而且是没有必要的

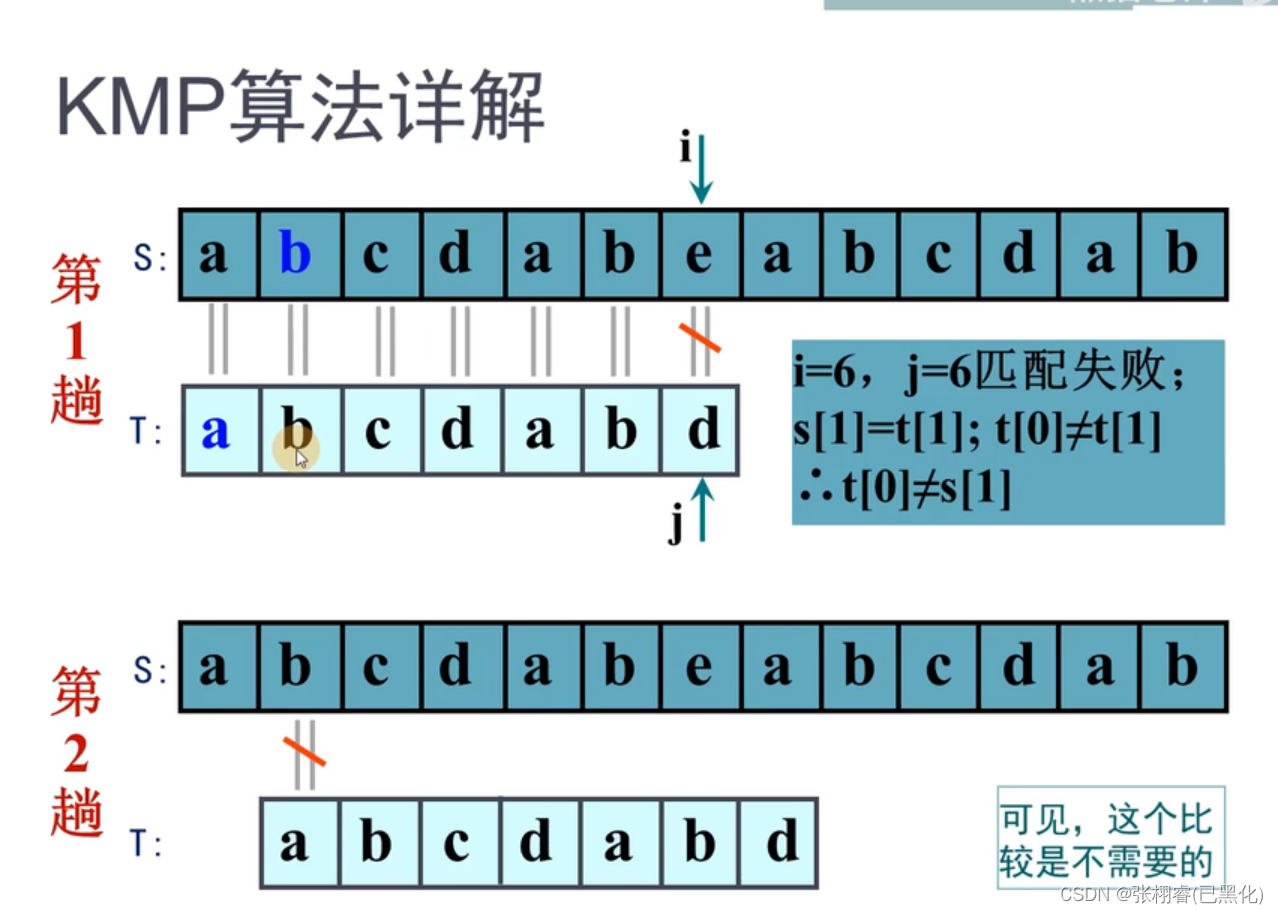
 所以我们通过KMP算法省去这些多余的比较。

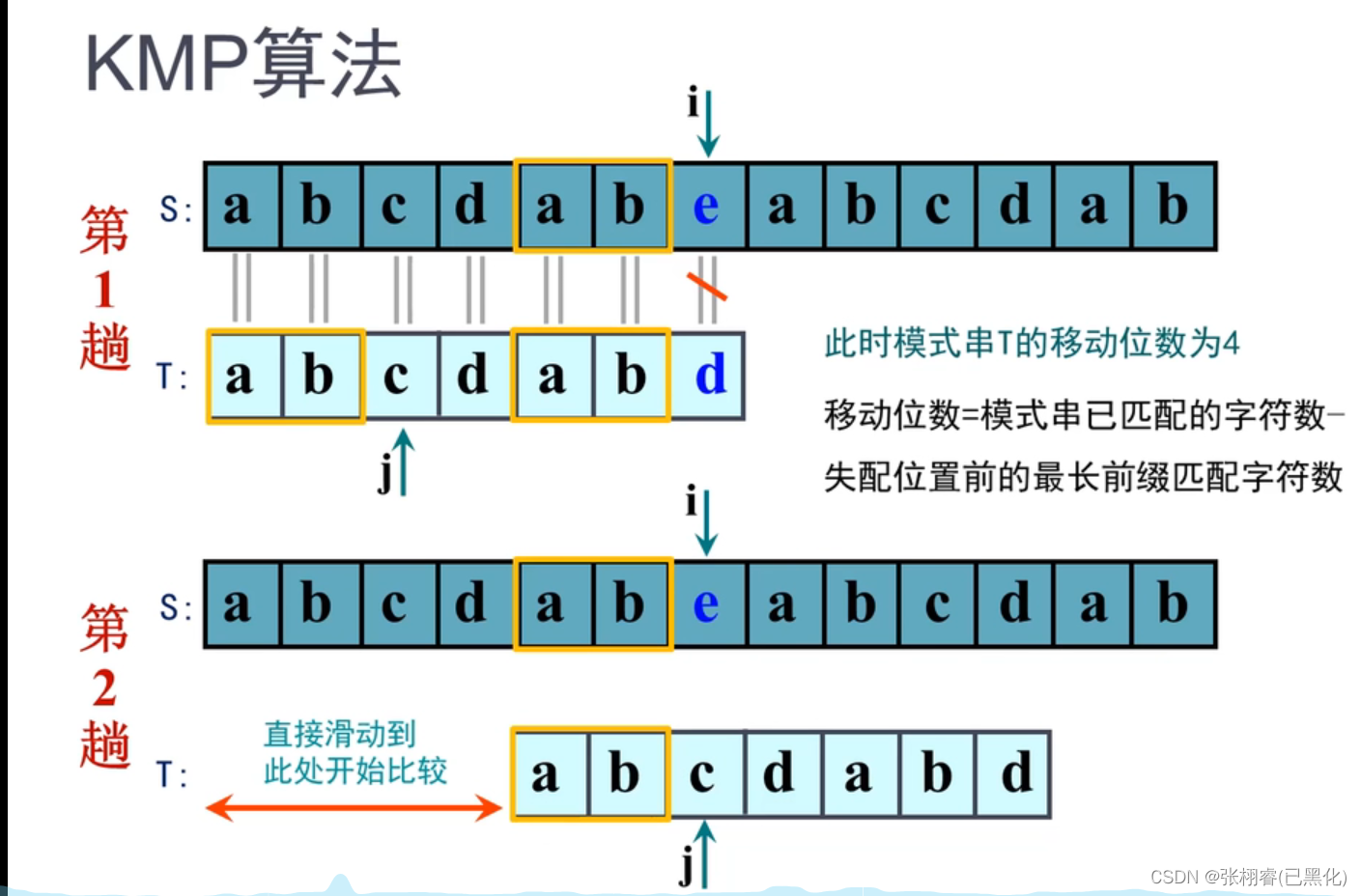
        同学们可能对于移动位数不太理解，其实这些移动的位数就是在我之前说的next数组里面存着的每个元素。

下面，我们就来讲述一下这个奇妙的next数组。

二.next数组的介绍及实现

        什么是next数组呢？实际上，next就是根据字串sub重复的字符构造出来的数组。next的长度和字串的长度是相同的。

 可能看到这里，同学们还是有点蒙，没关系我在来解释一下：

        我们先让next数组与字串sub对齐。只需要找到next数组对应的该位置前缀（前缀不包括该位置的字符）最长的两个相同字串，这两个相同字串的长度就是这个next的值。

我们再来看一个例子：

        对于下标为4的子串，我们发现，sub子串a==a，长度为一，所以下标为4的next数组填入4，同理，下标为5的子串 ，sub子串ab==ab，长度为2，所以我们填入2.。。。。所以我们只需要找到该位置前缀，以字串第一个字符开头，以该位置前一个位置的字符作为结束的字符串即可。

ok，下面咱们分三种情况来讲 next 的求解过程

特殊情况
当 j 的值为 0 或 1 的时候，它们的 k 值都为 0，即 next[0] = 0、next[1] =0。但是为了后面 k 值计算的方便，我们将 next[0] 的值设置成 -1。

当 t[j] == t[k] 的情况
举个栗子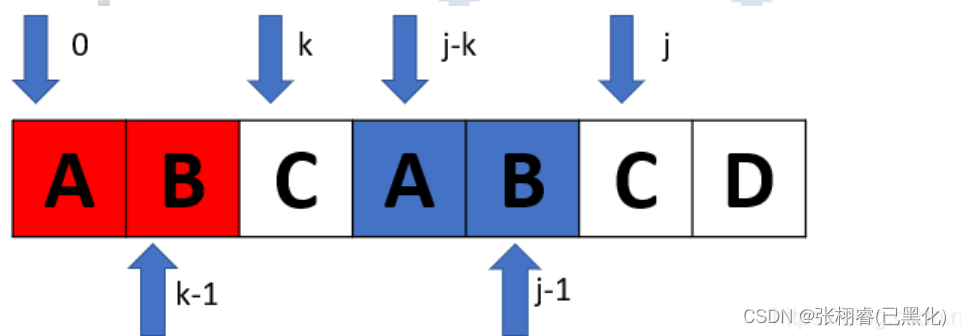

        观察上图可知，当 t[j] == t[k] 时，必然有"t[0]…t[k-1]" == " t[j-k]…t[j-1]"，此时的 k 即是相同子串的长度。因为有"t[0]…t[k-1]" == " t[j-k]…t[j-1]"，且 t[j] == t[k]，则有"t[0]…t[k]" == " t[j-k]…t[j]"，这样也就得出了next[j+1]=k+1。

当t[j] != t[k] 的情况
        关于这种情况，在代码中的描述就是“简单”的一句 k = next[k]；为什么呢？如果我们的t[j] != t[k]，就已经说明之前的t[0]…t[k]" == " t[j-k]…t[j]发生了断裂，不知道大家有没有发现next数组的规律，都是递增，然后突然变为0或1，并且回溯的时候，除了回溯到的第一个元素，其他元素和回溯之前的元素都是一样的！所以回溯的意义其实是找到首元素！下面我会优化这段代码。

void GetNext(int* next, char* sub)
{
	next[0] = -1;
	if (strlen(sub) == 1)
		return;
	next[1] = 0;
	int k = 0;
	int i = 2;
	while (i < strlen(sub))
	{
		if ((k==-1)||sub[i - 1] == sub[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else
		{
			k = next[k];
		}
	}
}

三.next数组的优化

        上面我们发现，next数组回溯以后得到的元素，和该元素是一样的，而且本质上next数组的意义就是找到首元素！所以我们可以把刚刚的代码优化并且可以更容易理解！

void GetNext(int* next, char* sub)
{
	next[0] = -1;
	if (strlen(sub) == 1)
		return;
	next[1] = 0;
	int k = 0;
	int i = 2;
	while (i < strlen(sub))
	{
		if (sub[i - 1] == sub[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else if(sub[0]==sub[i-1])
		{
			sub[i]=1;
			i++;
			k++;
		}
		else if (sub[0] != sub[i - 1])
		{
			sub[i] = 0;
			i++;
			k++;
		}
	}
}

四.伪代码和完整代码的实现

原代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<string.h>
#include<stdlib.h>
//str主串
//sub子串
//pos从主串哪里开始找
void GetNext(int* next, char* sub)
{
	next[0] = -1;
	if (strlen(sub) == 1)
		return;
	next[1] = 0;
	int k = 0;
	int i = 2;
	while (i < strlen(sub))
	{
		if (sub[i - 1] == sub[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else if(sub[0]==sub[i-1])
		{
			sub[i]=1;
			i++;
			k++;
		}
		else if (sub[0] != sub[i - 1])
		{
			sub[i] = 0;
			i++;
			k++;
		}
	}
}
int KMP(char* str, char* sub, int pos)
{
	assert(str && sub);
	int lenstr = strlen(str);
	int lensub = strlen(sub);
	if (pos < 0 || pos >= lenstr)return -1;
	int* next = (int*)malloc(sizeof(int) * lensub);
	GetNext(next, sub);
	int i = pos;
	//遍历主串
	int j = 0;
	//遍历字串
	while (i < lenstr && j < lensub)
	{
		if ((j == -1) || (str[i] == sub[j]))
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];
		}
	}
	free(next);
	if (j >= lensub)
		return i - j;
	return -1;
}
int main()
{
	printf("%d", KMP("abcabcaad", "ad", 0));
}

总结：       

        KMP算法是鹏哥让我们课余时间研究的一个算法，虽然弄懂她花了我好多时间，但是真正搞清楚以后就非常的开心。辛苦各位小伙伴们动动小手，三连走一波 最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！