离散时间信号的分析

实验项目	离散时间信号的分析
实验类别	基本性实验	实验学时	4学时
实验目的及设备	一、实验目的 认识常用的各种信号，理解其数学表达式和波形表示。 掌握在计算机中生成及绘制数字信号波形的方法。 掌握序列的简单运算及计算机实现与作用。 理解离散时间傅立叶变换、Z变换及它们的性质和信号的频域特性。 二、实验设备 计算机，MATLAB语言环境。

预  习

实验基础理论： 1.序列的概念  序列是时间上不连续的一串样本值的集合{x(n)},n为整形变量，x(n)表示序列中的第n个样本值 2.常见序列 (1）单位脉冲序列 (2）单位阶跃序列 (3）矩形序列 (4）实指数序列 (5）正弦序列 (6）复指数序列 3.序列的基本运算 ◆ 序列加法     序列加法是指把两个序列  、 中同序号的序列值逐项对应相加，形成新的序列 ◆ 序列乘法      序列乘法是指把两个序列 、 中同序号的序列值逐项对应相乘，形成新的序列   序列的乘法是一种非线性运算，它用于信号的调制 ◆ 序列的倍乘 序列倍乘是指把序列x(n)中所有序号下的序列值同乘一个常数 a ◆ 序列移位 、翻转及尺度变换 当n0>0时，序列右移n0个序数，称为x(n) 的延时序列 当n0<0时，序列左移n0个序数，称为x(n) 的超前序列 4.离散傅里叶变换的相关概念 离散傅里叶变换（DFT），是傅里叶变换 在时域和频域上都呈现离散的形式，将时域信号的采样变换为在离散时间傅里叶变换（DTFT）频域的采样。 在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。 5.Z变换的相关概念（4、5的关系？） Z变换（Z-transformation）是对离散序列进行的一种数学变换，常用于求线性时不变差分方程的解。它在离散系统中的地位如同拉普拉斯变换在连续系统中的地位。 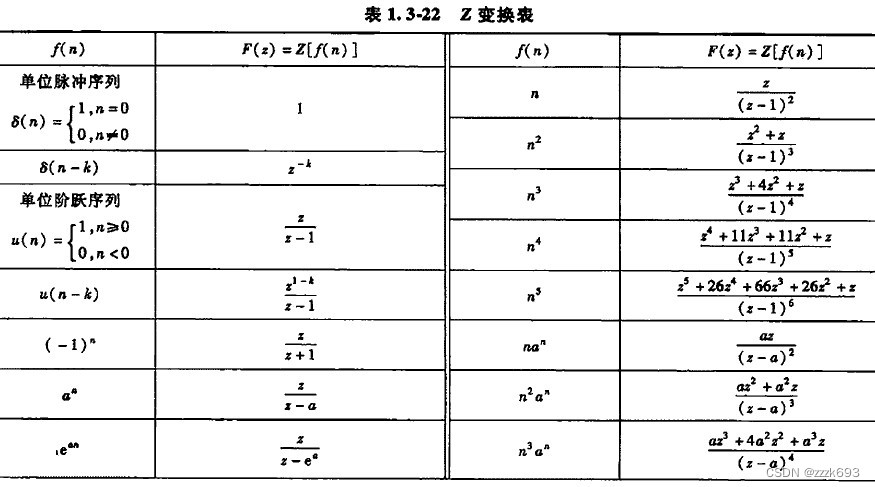Z变换是傅里叶变换的推广,当傅里叶变换不存在时,Z变换所定义的幂级数可能收敛。傅里叶变换是在单位圆上的Z变换,也就相当于在概念上把线性频率轴缠绕在单位圆上,因此傅里叶变换在频率上的固有周期性就自然得到了。 Z变换公式中,令,可以得到离散序列的傅里叶变换与Z变换的关系:再根据Z反变换,将积分围线取在单位圆上,得:可见,Z平面单位圆上的一周正好对应的一个周期。

实 验 内 容

(说明：此部分应包含：实验内容、实验步骤、实验数据与分析过程等) 一、离散时间信号（序列）的产生 利用MATLAB语言编程产生和绘制单位样值信号、单位阶跃序列、指数序列、正弦序列及随机离散信号的波形表示。 （1）单位样值信号： 代码：   波形： （2）单位阶跃序列： 代码： 波形： （3）指数序列： 代码： 波形： （4）正弦序列： 代码： 波形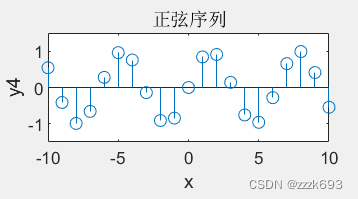： （5）随机离散信号： 代码： 波形： 二、序列的运算 （１）利用ＭＡＴＬＡＢ语言编程实现信号平滑运算。 smooth(y)可得到 平滑处理后的曲线序列y，并且可以迭代使用，多次使用平滑效果更加明显。 代码： 波形： （２）利用MATLAB语言编程实现信号的调制。 常见的模拟调制方式有幅度（线性）调制和角度（非线性）调制，其中幅度调制包括：调幅（AM）、双边带（DSB）、单边带（SSB）和残留边带（VSB）等调制方式。 产生一个频率为1Hz、功率为1的余弦信源（设载波频率为10Hz） a.A=2的AM调制    代码： clc,clear,close all; dt=0.001; t=-10:dt:10;% 仿真时间 A=2; fm=1;%基带信号频率 fc=10;%载波频率 fm = 0.3; % 带通滤波器通带 mt=sqrt(2)*cos(2*pi*fm*t);%基带信号 c=cos(2*pi*fc*t);%载波信号 st_AM=(mt+A).*c;%AM %绘制基带信号 subplot(221) plot(t,mt) xlabel('t'); ylabel('mt'); %plot(t,mt,'r--') title('基带信号波形'); axis([-5,5,-1.5,1.5]); grid on; %绘制AM波形 subplot(222) plot(t,st_AM) xlabel('t'); ylabel('st_AM'); hold on; plot(t,mt+2,'r--'); title('AM调制波形'); legend('AM','基带信号') axis([-5,5,-5,5]); grid on; 波形结果： b.双边带（DSB）调制： clc,clear,close all; dt=0.001; t=-10:dt:10; % 仿真时间 fm=1;%基带信号频率 fc=10;%载波频率 mt=sqrt(2)*cos(2*pi*fm*t);%基带信号 c=cos(2*pi*fc*t);%载波信号 st=mt.*c;%DSB %绘制基带信号 subplot(223) plot(t,mt) xlabel('t'); ylabel('mt'); %plot(t,mt,'r--') title('基带信号波形'); axis([-5,5,-1.5,1.5]); grid on; subplot(224) plot(t,st) xlabel('t'); ylabel('st'); hold on; plot(t,mt,'r--'); title('DSB调制波形'); legend('DSB','基带信号') axis([-5,5,-1.5,1.5]); grid on; 波形： 单边带（SSB）调制： clc,clear,close all; dt=0.001; t=-10:dt:10;% 仿真时间 fm=1;%基带信号频率 fc=10;%载波频率 mt=sqrt(2)*cos(2*pi*fm*t);%基带信号 c=cos(2*pi*fc*t);%载波信号 st=real(hilbert(mt).*exp(j*2*pi*fc*t));%SSB Hilbert（希尔伯特）变换 %绘制基带信号 subplot(411) plot(t,mt) xlabel('t'); ylabel('mt'); title('基带信号波形'); axis([-5,5,-2,2]); grid on; %绘制SSB波形 subplot(412) plot(t,st) xlabel('t'); ylabel('st'); hold on; plot(t,mt,'r--'); title('SSB调制波形'); legend('SSB','基带信号') axis([-5,5,-2,2]); grid on; 波形： 构建函数fftseq代码： 频率调制： 代码： %% 频率调制 FM clear all;close all; t0 = 0.15;%信号保持时间 ts = 0.0005;%采样时间 fc = 200;%载波频率 kf = 50;%调制系数 fs = 1/ts;%采样频率 df = 0.25;%频率分辨率 t_v = [0:ts:t0];%时间序列 m = [ones(1,t0/(3*ts)),-2*ones(1,t0/(3*ts)),zeros(1,t0/(3*ts)+1)];%消息信号m(t)，t/ts是序列的数目。注意端点，要+1 m_int(length(m)) = 0; %以下两种方法都可实现对m(t)的积分。法二更直观，一定要乘以ts！ for i = 1:length(m)-1     m_int(i+1) = m_int(i) + m(i)*ts; end % for i = 1:length(m) %     m_int(i) = ts*sum(m(1:i)); % end [M,m,df1] = fftseq(m,ts,df);%傅里叶变换 M = M/fs; f = [0:df1:df1*(length(m)-1)]-fs/2;%画[-fs/2,fs/2]的图像 u = cos(2*pi*fc*t_v + 2*pi*kf*m_int);%调制信号 figure plot(t_v,u) [U,u,df1] = fftseq(u,ts,df);%傅里叶变换 U = U/fs; %画图 figure; subplot(221);plot(t_v,m(1:length(t_v)));%经过fftseq函数后，m的长度与t_v的长度不一定相等，但有效长度相等 axis([0 0.15 -2.1 2.1]); xlabel('时间');title('消息信号') subplot(222);plot(t_v,u(1:length(t_v))) axis([0 0.15 -2.1 2.1]); xlabel('时间');title('调频信号') subplot(223);plot(f,abs(fftshift(M))); xlabel('频率');title('消息信号频谱') subplot(224);plot(f,abs(fftshift(U))); xlabel('频率');title('调制信号频谱') 结果： 相位调制： 代码： clear all;close all; t0 = 0.25;%信号保持时间 ts = 0.0005;%采样时间 fc = 200;%载波频率 fs = 1/ts;%采样频率 df = 0.25;%频率分辨率 t_v = [0:ts:t0];%时间序列 m(length(t_v)) = 0; lent = length(t_v)-1; for i = 1:(t0/ts/4)     m(i) = i; end for i = (lent/4+1):3*(lent/4)     m(i) = m(lent/4) - i+lent/4; end for i = (3*lent/4+1):lent+1     m(i) = m(3*lent/4) + i-lent*3/4 end m = m/50; [M,m,df1] = fftseq(m,ts,df);%傅里叶变换 M = M/fs; f = [0:df1:df1*(length(m)-1)]-fs/2;%画[-fs/2,fs/2]的图像 u = cos(2*pi*fc*t_v + m(1:length(t_v)));%调制信号 [U,u,df1] = fftseq(u,ts,df);%傅里叶变换 U = U/fs; %画图 figure; subplot(221);plot(t_v,m(1:length(t_v)));%经过fftseq函数后，m的长度与t_v的长度不一定相等，但有效长度相等 axis([0 0.25 -3 3]); xlabel('时间');title('消息信号') subplot(222);plot(t_v,u(1:length(t_v))) axis([0 0.15 -2.1 2.1]); xlabel('时间');title('调频信号') subplot(223);plot(f,abs(fftshift(M))); xlabel('频率');title('消息信号频谱') subplot(224);plot(f,abs(fftshift(U))); xlabel('频率');title('调制信号频谱') 结果： （３）利用MATLAB语言编程实现信号卷积运算。 可使用Conv函数来计算卷积和多项式乘法，用法:w = conv(u,v)，返回向量u和v的卷积。 代码： a=[4 5 6]; b=[1 2 3]; y=conv(a,b); 结果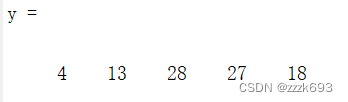： （４）利用MATLAB语言编程实现信号离散傅立叶的正反变换。 信号离散傅立叶变换： 构造函数： 信号离散傅立叶反变换： 构造函数： 代码： clc;clear;close all; xn = [0,1,2,3]; N = 4; Xk = dft(xn,N);  figure; subplot(221);plot(Xk); axis([-10 10 -5 5]); xn = idft(Xk,N) subplot(222);plot(xn); axis([-10 10 -5 5]); 结果： 利用MATLAB语言编程实现信号的圆周移位、圆周卷积，验证DFT 的圆周时移、圆周卷积性质和圆周卷积与线性卷积的关系。 Circshift函数可实现序列的圆周移位 x=0:3;       y=[1 2 3 4];       subplot(2,2,1);       stem(x,y);       xlabel('x');       ylabel('y');       title('原序列');             subplot(2,2,2);       y=circshift(y,1,2);       stem(x,y);       xlabel('x');       ylabel('y');       title('圆周移位1次');             subplot(2,2,3);       y=circshift(y,1,2);       stem(x,y);       xlabel('x');       ylabel('y');       title('圆周移位2次');             subplot(2,2,4);       y=circshift(y,1,2);       stem(x,y);       xlabel('x');       ylabel('y');       title('圆周移位3次'); 结果： 圆周卷积： 线性卷积： 线性时不变系统输入、输出间的关系为：当系统输入序列为x(n) ，系统的单位脉冲响应为h(n)，输出序列为y(n)，则系统输出为： 上式称为线性卷积 构建的卷积函数： 线性卷积代码： nx=0:3;      x=(nx+1); nh=0:3;     h=4-nh; ny=0:6;    y=conv(x,h); figure;  subplot(3,1,1); stem(nx,x); xlabel('n');ylabel('x(n)'); subplot(3,1,2);  stem(nh,h); xlabel('n');ylabel('h(n)'); subplot(313);  stem(ny,y); xlabel('n');ylabel('y(n)'); title('线性卷积'); 结果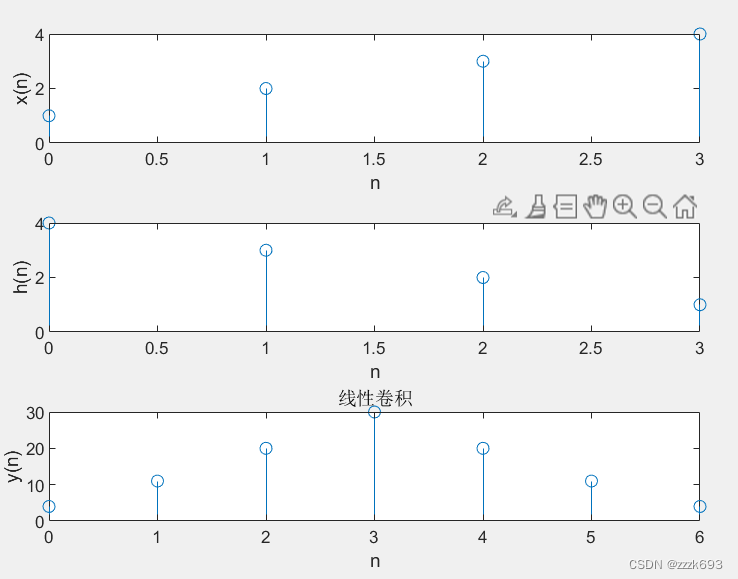： 循环卷积代码： nx=0:3;     x=(nx+1); nh=0:3;     h=4-nh; yc5=circonv([x,0],[h,0]);            yc6=circonv([x,0,0],[h,0,0]); yc7=circonv([x,0,0,0],[h,0,0,0]); yc8=circonv([x,0,0,0,0],[h,0,0,0,0]); figure; subplot(2,2,1);stem(0:4,yc5);  title('循环卷积yc5'); subplot(2,2,2);stem(0:5,yc6);  title('循环卷积yc6'); subplot(2,2,3);stem(0:6,yc7);  title('循环卷积yc7'); subplot(2,2,4);stem(0:7,yc8);  title('循环卷积yc8'); 结果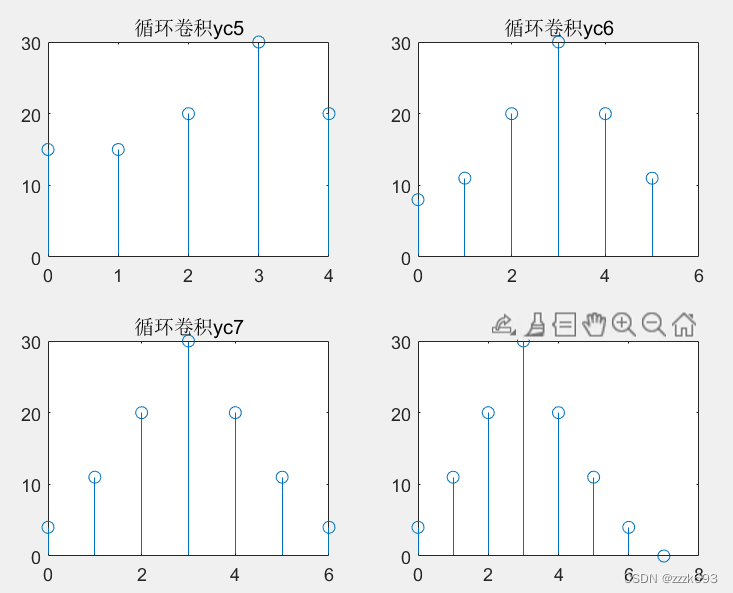： 循环卷积（圆周卷积）与线性卷积的关系： 验证一个周期实序列奇偶部分的DFT与此序列本身的DFT之间的关系。 对x=sin(pi*n/8)+sin(pi*n/4) 进行DFT 分别显示其原函数、幅度和相位的分布图 原序列 代码： N=16; n=0:N-1;k=n; x=sin(pi*n/8)+sin(pi*n/4); y=x*exp(-j*2*pi/N).^(n'*k); subplot(3,1,1);stem(n,x,'filled');ylabel('x'); subplot(3,1,2);stem(k,abs(y),'filled');ylabel('mag X(k)'); subplot(3,1,3);stem(k,angle(y),'filled');ylabel('ang X(k)'); 结果： 偶数部分DFT： 代码： N=16; n=[0:2:N-1];k=n; x=sin(pi*n/8)+sin(pi*n/4); y=x*exp(-j*2*pi/N).^(n'*k); subplot(3,1,1);stem(n,x,'filled');ylabel('x'); subplot(3,1,2);stem(k,abs(y),'filled');ylabel('mag X(k)'); subplot(3,1,3);stem(k,angle(y),'filled');ylabel('ang X(k)'); 结果： 奇数部分DFT： 代码： N=16; n=[1:2:N-1];k=n; x=sin(pi*n/8)+sin(pi*n/4); y=x*exp(-j*2*pi/N).^(n'*k); subplot(3,1,1);stem(n,x,'filled');ylabel('x'); subplot(3,1,2);stem(k,abs(y),'filled');ylabel('mag X(k)'); subplot(3,1,3);stem(k,angle(y),'filled');ylabel('ang X(k)'); 结果： 利用MATLAB语言编程实现信号的Z变换及其反变换、Z变换的零、极点分布。 代码： syms n; f=(1/2)^n+(1/3)^n; F=ztrans(f); syms z; F=2*z/(z-2)^2; f=iztrans(F) 结果：      代码： B=[1,0.32]; A=[1,1,0.16]; [R,P,K]=tf2zp(B,A) 结果：   则零点为z=0.32，极点为p1=0.8,p2=0.2; 五、实验扩展与思考   1. 编程产生方波信号序列和锯齿波信号序列。 x = sawtooth(t,xmax)产生锯齿波序列，有两个参数，其中第二个参数xmax可省略。 该函数周期为2 π 2\pi2π，t是时间刻度序列，xmax是刻度伸缩系数，介于0到1之间，默认为1，默认幅度从-1到+1锯齿上升。 x = square(t,duty)与sawtooth函数类似，周期为2 π 2\pi2π，t是时间刻度序列，duty是占空比。 代码： A = input('The peak value =');%峰值7 L = input('Length of sequence =');%序列长度100 N = input('The period of sequence =');%序列重复周期13 FT = input('The desired sampling frequency =');%采样频率20000 DC = input('The square wave duty cycle = ');%波形占空比60 % Create signals T = 1/FT;%采样时间间隔 n = 0:L-1;%序列的序号 x = A*sawtooth(2*pi*n/N);%产生周期为N的锯齿波 y = A*square(2*pi*(n/N),DC);%产生周期为N，占空比为DC的方波 % Plot subplot(211) stem(n,x); ylabel('Amplitude'); xlabel(['Time in ',num2str(T),'sec']); subplot(212) stem(n,y); ylabel('Amplitude'); xlabel(['Time in ',num2str(T),'sec']); 结果： 上面是幅度为6的锯齿波，下面是幅度为6，占空比为60%的方波（的数字采样信号）   2. 实验中你所产生得正弦序列的频率是多少？怎样才能改变它？分别是哪些参数控制该序列的相位、振幅和周期？  产生的正弦序列的角频率是1，可通过改变f的值来改变正弦序列的频率；参数phase控制该序列的初相位；参数A控制振幅，T控制周期。   3. 编程实现序列长度为N的L点的正反离散傅里叶变换，并分析讨论所得出的结果，其中L≥N，如L=8，N=6。 可以使用内置函数fft和ifft来实现正反离散傅里叶变换（DFT和IDFT）。 代码： % 定义输入序列长度为N N = 6; x = [1, 2, 3, 4, 5, 6]; % 填充输入序列到长度L L = 8; x_padded = [x, zeros(1, L - N)]; % 计算DFT X = fft(x_padded); % 计算IDFT x_reconstructed = ifft(X); % 显示原始序列 subplot(3, 1, 1); stem(0:N-1, x, 'r', 'LineWidth', 1.5); title('原始序列'); xlabel('时域索引'); ylabel('Amplitude'); % 显示DFT结果 subplot(3, 1, 2); stem(0:L-1, abs(X), 'b', 'LineWidth', 1.5); title('DFT结果'); xlabel('频域索引'); ylabel('幅度'); % 显示IDFT结果 subplot(3, 1, 3); stem(0:L-1, real(x_reconstructed), 'g', 'LineWidth', 1.5); title('IDFT结果'); xlabel('时域索引'); ylabel('Amplitude'); % 调整图形布局 sgtitle('正反离散傅里叶变换结果'); % 显示图形 figure; 结果： 在分析结果时，可以观察以下几点： DFT结果（X）：X是输入序列x在频域的表示。它包含了原始信号的幅度和相位信息。 IDFT结果（x_reconstructed）：x_reconstructed是DFT结果X进行逆变换得到的序列。它应该与原始序列x相匹配。 零填充的影响：在DFT中，我们对输入序列进行了零填充，这意味着在频域中我们对信号进行了插值。在IDFT中，我们将这个填充的效果去除，得到了与原始信号相似但长度为L的序列。 通过观察这些结果，可以更好地理解DFT和IDFT之间的关系，以及零填充对频域和时域表示的影响。   4. 由实验说明离散傅里叶变换的对称关系，说明序列的时域和频域的关联特性。 代码： % 创建一个简单的序列 x = [1, 2, 3, 4]; % 计算DFT X = fft(x); % 获取序列长度 N = length(x); % 绘制原始序列和DFT结果的幅度 subplot(2, 2, 1); stem(0:N-1, x); title('时域序列'); xlabel('时域样本索引'); ylabel('幅度'); subplot(2, 2, 2); stem(0:N-1, abs(X)); title('频域序列 (幅度)'); xlabel('频域样本索引'); ylabel('幅度'); % 计算DFT结果的相位 phaseX = angle(X); % 绘制DFT结果的相位 subplot(2, 2, 3); stem(0:N-1, phaseX); title('频域序列 (相位)'); xlabel('频域样本索引'); ylabel('相位'); % 绘制DFT结果的对称性 subplot(2, 2, 4); stem(0:N-1, abs(X)); hold on; stem(0:N-1, flip(abs(X)), 'r'); title('DFT结果的对称性'); xlabel('频域样本索引'); legend('正频率', '负频率'); % 调整图形窗口大小 set(gcf, 'Position', get(0, 'Screensize')); % 显示图形 grid on; 结果： 时域序列（图1）的幅度在频域（图2）中找到对应的频率成分，其相位信息在频域（图3）中展示。 频域序列 X（图2）在正频率和负频率上是对称的。这是DFT的一个重要性质，即 X[k] = X[N-k]，其中 N 是序列的长度。这个对称性关系在图4中也有所展示，其中正频率和负频率部分的幅度在相对位置上是对称的。

实 验 总 结

（说明：总结实验认识、过程、效果、问题、收获、体会、意见和建议。） 通过本次实验，我更加深入的理解了如何借助matlab在计算机中生成及绘制数字信号波形，掌握了序列的简单运算及计算机实现与作用，同时理解了离散时间傅立叶变换、Z变换及它们的性质和信号的频域特性，实验的图形清晰的表示了序列的相加、相乘、移位、反折等的形成，这使得我能更形象地了解信号变化的具体过程，基本达成本次实验目标。 在实验过程中，我遇到了些许问题，在验证一个周期实序列奇偶部分的DFT与此序列本身的DFT之间的关系时遇到了困难，通过翻看课本、网上查阅相关资料与同学讨论，于是我采取将复指数函数分解为用幅度与相位角两方面来分析考虑，最后得到验证结果。通过在错误中不断学习，我对matlab语言以及其基本语言规范有了更深入的了解，如：matlab中函数表达式不可省略符号“a*b”不能简写为“ab”,并学习了新的函数，如smooth(y)可得到 平滑处理后的曲线序列y，并且可以迭代使用；Abs（）：取绝对值和复数的模；angle()：取相位角；imag（）：取复数的虚部等；同时了解到了fft()和fftshift()的区别：M =fft(m)是对消息信号m(t)进行快速FFT变换，得到取值范围为(0,fs)的函数M(f)，如果想画出取值范围为(-fs/2,fs/2)的函数时，需要用到 fftshift0)函数。