OTFS调制，及其与OFDM的对比

了了J

已于 2025-03-31 22:33:13 修改

阅读量1.1k

点赞数 30

文章标签：网络

于 2025-03-25 09:57:00 首次发布

本文链接：https://blog.csdn.net/qq_74921796/article/details/146475242

版权

#参考于matlab2024版的帮助文档https://ww2.mathworks.cn/help/comm/ug/otfs-modulation.html#

一、前言

此例子模拟了使用正交时频空间（OTFS）调制的通信链路，并与标准正交频分复用（OFDM）调制进行对比，突出了其消除载波间干扰（ICI）的能力。OTFS是一种多载波调制技术，在由高多普勒多径组成的信道环境中具有适应力。大多数现代无线系统使用OFDM，由于无法消除ICI，在高多普勒信道中会受到影响。该示例实现了一个简单的OTFS发射机和接收机，通过具有移动散射体的信道对数据进行滤波，并使用估计的信道参数在延迟多普勒（DD）域中对信道进行均衡，以检测传输的码字。

二、OTFS的基本原理

在高多普勒信道中，信道特性的变化非常迅速，导致信道的相干时间低。相干时间与信道参数变化成反比。多年来，OFDM一直是各种无线系统的首选调制方案。使用OFDM，在高多普勒信道环境中需要频繁的进行信道测量减少ICI。OFDM在高多普勒信道环境中的两个缺点包括需要更频繁的进行信道测量和ICI：

.OFDM在时频（TF）域中传输数据，每个数据符号在其自己的正交频率子载波中。参考（导频）符号能够进行信道测量，但会占用部分传输带宽。由于信道特性的快速变化，导频必须频繁传输。这些导频取代了数据，从而降低了吞吐量。

.当各个路径由于散射体的不同相对速度而具有不同的频率偏移时，OFDM在高多普勒多径信道中会受到ICI的影响。来自不同路径的频率偏移破坏了无干扰符号检测所必需的频域正交性。

OTFS调制消除了频繁测量信道的需要，因为它在延迟多普勒域中传输数据。该域表示相对于接收机具有延迟（传输延迟）和速度（多普勒频移）的移动散射体。假设散射体的数量有限，则散射体的信道表示变为稀疏矩阵（除了表示散射体的少数非零条目外，延迟域信道矩阵大多为零）。高效的信道估计和均衡技术利用了这种稀疏性。此外，如果散射体保持稳定的速度，则信道在DD域中是准平稳的。对导频传输的需求减少，有效的增加了吞吐量。由于其对高多普勒信道的适应性，OTFS被视为5G NR和6G的调制候选者，以满足高速用例的新要求。

2.1、OTFS数据网格

在OTFS调制中，信息符号被映射到表示延迟多普勒域的M×N的二维传输数据网格Xdd[k,l]，其中k是延迟轴索引，k=0,1,...,M−1，l是多普勒轴索引，l=0,1...,N−1。此网格是一个OTFS符号，网格中的每一列都是一个子符号。索引k和l通过延迟=k/（M*df）和多普勒=l/（N*T）的关系与实际延迟和多普勒频移有关，其中df是以赫兹为单位的子载波间隔，T是包括任何循环前缀在内的OTFS子符号的持续时间（秒）。索引k和l是归一化延迟和归一化多普勒频偏。

2.2、延迟多普勒域

在延迟多普勒域中的操作类似于脉冲多普勒雷达信号处理中的雷达回波处理。雷达发射窄带脉冲，并根据返回信号的到达时间（通过传输和接收之间的延迟测量）和基于多普勒频移回波的速度将返回的回波分类到一定范围内。类似地，发射机可以向接收机发送具有多径反射的信号，就像雷达回波一样。由于反射器相对于接收器的运动，每个多径反射可能相对于发射器具有一定的延迟和一定的多普勒频移。在下图中，基站向位于移动汽车中的接收器发送信号。右上角所示的二维延迟多普勒信道响应Hdd表示具有相应路径号的各个路径。路径的数量和厚度的大小与路径强度成正比。

直接视线是参考时间，用0个样本延迟的粗线表示。汽车正以130公里/小时的速度向基站移动，但由于汽车中的接收器调整载波频率以补偿任何多普勒频移效应，因此该路径的多普勒频移指数为0。路径1表示来自比接收车慢的相邻卡车的反射。由于信号传输的距离较长，路径1的传输延迟稍长，并且由于汽车缓慢远离卡车，路径1具有负多普勒频移。路径2是来自救护车在更远距离向汽车移动的另一个反射，因此它具有正多普勒、更长延迟和更小的路径增益。

多路径对单个DD网格元素的影响如下所示。Xdd包含五个传输信号，Hdd是信道响应。Ydd是Xdd和Hdd的二维卷积。在OTFS中，时间有限信号意味着卷积是循环的，包括相位旋转，这被称为扭曲卷积。

2.3、延迟多普勒域到时频域的表示

为了解延迟多普勒域如何转换为时频域，可以将该过程与OFDM联系起来。下图显示了作为预编码OFDM调制解调系统的OTFS调制和解调。M等于OFDM符号中的子载波数量，N等于一帧中包含的OFDM符号数量。

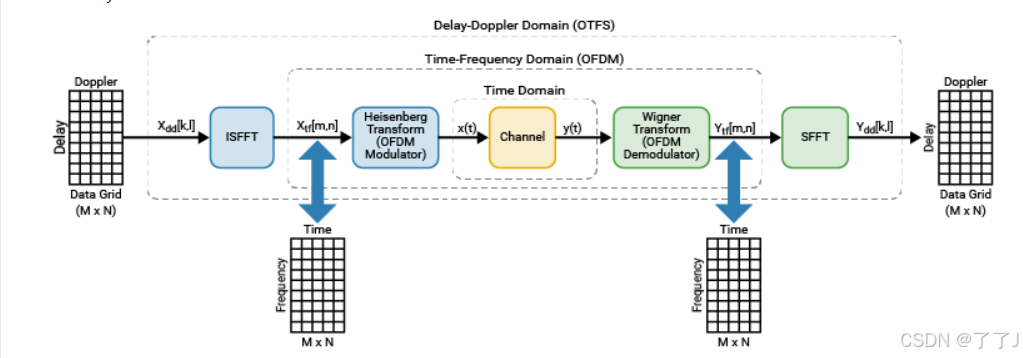
图的内部部分是OFDM调制器、信道和OFDM解调器的OFDM处理线路。海森堡变换和维格纳变换分别是OFDM调制器和OFDM解调器的推广。首先，辛有限傅里叶逆变换（ISFT）将调制信号从延迟多普勒域Xdd变换到时频域Xtf：

内部求和项是Xdd在多普勒轴上的离散傅里叶逆变换（IDFT）:

此操作将Xdd从延迟多普勒域转换到延迟时域，由Xdt表示。在MATLAB中，数组的DFT对每一列独立操作。IDFT应用于Xdd的转置，在多普勒轴上操作IDFT，然后对结果进行转置，使结果回到正确的阵列维度。

ISFT表达式中的外部求和项是延迟轴上的DFT：

所以ISFT可化简为：

（注：下文用到的helperOTFSdemod函数便是用这个公式写的）

此时，Xtf[m,n]表示为常见的时频域中的数据。海森堡变换将变换后的符号Xtf转换为时域信号Xt：

T是一个OFDM符号的持续时间。脉冲整形滤波器给g(t)减轻了由少数多普勒频移引起的信道扩展（当多普勒频率不在1/（NT）的倍数上时）。当滤波器是一个时间限制为0到T的矩形窗口时，海森堡变换只是一个在Xtf的每一列上工作的OFDM调制器。OTFS调制变为二维预编码OFDM调制，其中预编码操作是ISFT。ISFT是沿多普勒维度操作用于将其转换为时间维度的IDFT，以及沿延迟维度操作用于将它转换为频率维度的DFT。海森堡变换是一种沿频率维度运行的IDFT，相当于OFDM调制。

2.4、逆Zak变化

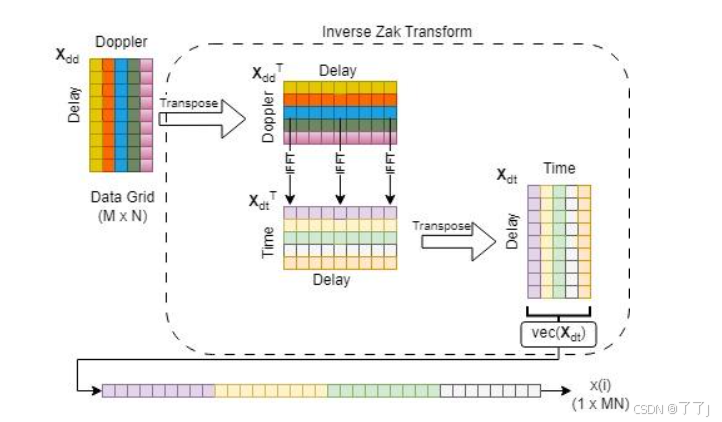
ISFT和海森堡变换的组合也可以使用逆Zak变换进行数学表示。它结合了ISFT和海森堡变换来消除IDFT-DFT对，从而将操作简化为多普勒轴上的IDFT。

回想一下，矩形脉冲整形将海森堡变换转换为普通的OFDM调制器，这只是Xtf中每列上的IFFT。则Xtf的IFFT为：

其中Xdt是输入数据的延迟时域表示。注意到IFFT-FFT组合抵消了每个操作，中间结果是逆Zak变换Xdt：

这一结果与之前使用ISFT和海森堡变换对得出的结果相同。逆Zak变换从Xdt[m,n]的矢量化表示输出离散化时域样本x(i)：

2.5、符号间干扰（ISI）的减少

在OTFS子符号或符号之间插入循环前缀或零序列以防止ISI，类似于OFDM使用循环前缀的方式。零填充（ZP）是一种ISI缓解技术，它为每个OTFS子符号附加长度为零的ZPLen样本。

循环前缀（CP）是一种在每个OTFS子符号前添加相应子符号的最后CPLen样本的技术。

缩减循环前缀（RCP）将OTFS符号的最后一个CPLen样本添加到符号的开头。缩减零填充（RZP）在OTFS符号的末尾附加ZPLen零。

三、OTFS在高移动性信道上的仿真

在延迟多普勒域中发送导频信号，以探测高移动性信道，并观察延迟多普勒域的信道响应。此示例使用零填充(cp)来演示信道探测和数据传输,并且只发送一个导频信号，其余为0。

3.1、仿真参数设置

配置仿真参数。为了演示基本的OTFS概念，设M=64，N=30。将信噪比设置为高值，以显示ISI和ICI在不同调制和信道条件下的影响。等概念理解更加深刻后，可以设置不同的信噪比用for循环得到误码率的曲线图。

M=64;           %子载波数
N=30;           %一帧中子符号数
df=15e3;        %子载波间隔
fc=5e9;         %载波中心频率
padLen=10;      %需要添加的前缀长度，需大于信道时延
padType='ZP';   %添零
SNRDB=40;       %设置大信噪比

3.2、用于信道测量的数据网格

创建一个大小为M×N的空数组，其中M行对应于延迟，N列对应到多普勒频偏。为了演示延迟多普勒域中的数据如何通过高移动性信道传播，在网格位置（1,16）放置导频信号以对信道进行检测。将其他网格元素留空，以便散射体回波出现在接收到的延迟多普勒网格中。

%产生导频用于检测信道响应,在(1,16)插入导频，其余为0
pilotBin=floor(N/2)+1;
Pdd=zeros(M,N);
Pdd(1,pilotBin)=exp(1i*pi/4);

3.3、OTFS调制

对单个导频符号的DD数据网格作为数据进行OTFS调制。使用helperOTFSmod函数在导频网格Pdd上操作逆Zak变换。

%OTFS调制
txout=helperOTFSmod(Pdd,padLen,padType);    
%此函数不是 MATLAB 内置函数，是来自工具箱（ Communications Toolbox 或第三方库）。
% 需确保 helperOTFSmod.m 文件存在于当前工作目录或 MATLAB 路径中




function [y,isfftout] = helperOTFSmod(x,padlen,varargin)
%HELPEROTFSMOD Modulate the delay-Doppler domain input signal
%
%   [Y,ISFFT] = HELPEROTFSMOD(X,PADLEN,PADTYPE) performs OTFS modulation
%   on X using a rectangular pulse shaping window and outputs the results
%   in Y. Specify X as an M-by-N array of real or complex values. M is
%   the number of subcarriers and N is the number of OTFS subsymbols.
%   X - OTFS grid (M x N)
%   PADLEN - CP or ZP length (in samples)
%   PADTYPE (optional)
%     'CP'   = cyclic prefix (default)
%     'RCP'  = reduced cyclic prefix
%     'ZP'   = zero padding
%     'RZP'  = reduced zero padding
%     'NONE' = no CP/ZP
%   Y - vector of time domain output with selected cyclic prefix of size
%   M*N+PADLEN if PADTYPE is RCP or RZP, or of size (M+PADLEN)*N if
%   PADTYPE is CP or ZP, else size M*N if PADTYPE is NONE
%   ISFFTOUT - TF domain output of size M-by-N produced during the
%   two-step OTFS modulation.
%
%   See also helperOTFSdemod and OTFSModulationExample.mlx.

%   Copyright 2023-2024 The MathWorks, Inc.

M = size(x,1);              %求矩阵x的行数
if isempty(varargin)
    padtype = 'CP';
else
    padtype = varargin{1};
end

% Inverse Zak transform
y = ifft(x.').' / M;

% ISFFT to produce the TF grid output
isfftout = fft(y);

% Add cyclic prefix/zero padding according to padtype
switch padtype
    case 'CP'
        % % CP before each OTFS column (like OFDM) then serialize
        y = [y(end-padlen+1:end,:); y];  % cyclic prefix
        y = y(:);                        % serialize
    case 'ZP'
        % Zeros after each OTFS column then serialize
        N = size(x,2);
        y = [y; zeros(padlen,N)];    % zero padding
        y = y(:);                    % serialize
    case 'RZP'
        % Serialize then append OTFS symbol with zeros
        y = y(:);                    % serialize
        y = [y; zeros(padlen,1)];    % zero padding
    case 'RCP'
        % Reduced CP
        % Serialize then prepend cyclic prefix
        y = y(:);                        % serialize
        y = [y(end-padlen+1:end); y];    % cyclic prefix
    case 'NONE'
        y = y(:);                   % no CP/ZP
    otherwise
        error('Invalid pad type');
end
end

3.4、高移动性信道

使用固定发射机和移动接收机以及不同延迟和多普勒频移的移动散射体创建AWGN高移动性信道：

.创建一条视线路径，表示从基站到接收器的主传播路径，具有零延迟和零归一化多普勒。视线路径具有零延迟和零多普勒，因为接收器在时间和频率上与基站同步。

.创建散射体1，延迟来自接收器的五个样本，并使用归一化多普勒的三倍多普勒远离接收器。

.创建散射体2，从接收器延迟八个样本，并以归一化多普勒的五倍多普勒向接收器移动。

%信道参数配置
chanParams.pathDelays=[0 5 8];      %时延
chanParams.pathGains=[1 0.7 0.5];   %增益
chanParams.pathDopplers=[0 -3 5];   %多普勒频偏

assert(strcmp(padType,'ZP'),'Example must ZP pad type');
%加入cp或zp时，参数如下

fsamp=M*df;             %符号带宽，奈奎斯特速率下的采样率
Meff=M+padLen;          %一个OTFS子符号的样本数
numSamps=Meff*N;        %一个OTFS符号的样本数
T=((M+padLen)/(M*df));  %符号时间

%从多普勒索引中计算实际的多普勒频移，chanParams结构体的参数都很重要
chanParams.pathDopplerFreqs=chanParams.pathDopplers*1/(N*T);    %doppler=l/NT

%OTFS调制信号通过信道
dopplerOut=dopplerChannel(txout,fsamp,chanParams);

%加入高斯白噪声
Es=mean(abs(pskmod(0:3,4,pi/4).^2));
no=Es/(10^(SNRDB/10));
chOut=awgn(dopplerOut,SNRDB,'measured');

(注：Es=mean(abs(pskmod(0:3,4,pi/4).^2));no=Es/(10^(SNRDB/10));计算的是单位符号下的信号平均功率与信号噪声，没用实际的意义，应该换成实际信号进行计算功率，求得实际的噪声功率，在后续进行信道估计时更加准确)

dopplerChannel函数为：

function y = dopplerChannel(x,fs,chanParams)
    % Form an output vector y comprising paths of x with different
    % delays, Dopplers, and complex gains
    numPaths = length(chanParams.pathDelays);
    maxPathDelay = max(chanParams.pathDelays);
    txOutSize = length(x);
    
    y = zeros(txOutSize+maxPathDelay,1);
    
    for k = 1:numPaths
        pathOut = zeros(txOutSize+maxPathDelay,1);

        % Doppler
        pathShift = frequencyOffset(x,fs,chanParams.pathDopplerFreqs(k));
    
        % Delay and gain
        pathOut(1+chanParams.pathDelays(k):chanParams.pathDelays(k)+txOutSize) = ...
            pathShift * chanParams.pathGains(k);
            
        y = y + pathOut;
    end
end

根据归一化的延迟与多普勒频偏，可以计算出实际的延迟与多普勒频偏并打印出来。

%打印实际的延时与多普勒频移
for k = 1:length(chanParams.pathDelays)
    fprintf('Scatterer %d\n',k);
    fprintf('\tDelay = %5.2f us\n', 1e6*chanParams.pathDelays(k)/(Meff*df));
    fprintf('\tRelative Doppler shift = %5.0f Hz (%5.0f km/h)\n', ...
        chanParams.pathDopplerFreqs(k), (physconst('LightSpeed')*chanParams.pathDopplerFreqs(k)/fc)*(3600/1000));
end                         %dopplerf=(v/c)*fc,v=(dopplerf*c)/fc

结果为：

Scatterer 1
   Delay = 0.00 us
   Relative Doppler shift = 0 Hz ( 0 km/h)
Scatterer 2
   Delay = 4.50 us
   Relative Doppler shift = -1297 Hz ( -280 km/h)
Scatterer 3
   Delay = 7.21 us
   Relative Doppler shift = 2162 Hz ( 467 km/h)

3.5、OTFS解调

为了开始解调过程，将接收到的信号向量打包到M×N的矩阵Ydt中。维格纳变换是海森堡变换的逆变化。因为这个例子使用了矩形脉冲整形，所以维格纳变换只是一个OFDM解调操作。在维格纳变换之后，SFFT将时频域网格转换为延迟多普勒域。在这个例子中，使用更有效的Zak变换来解调信号：

（注：helperOTFSdemod函数就是用到这个公式）

在OTFS帧中收集样本，并在延迟多普勒域中解调信号：

%截取信号有效长度
rxIn=chOut(1:numSamps);

%OTFS解调
Ydd=helperOTFSdemod(rxIn,M,padLen,0,padType);




function [y,tfout] = helperOTFSdemod(x,M,padlen,offset,varargin)
%HELPEROTFSDEMOD OTFS demodulate the time-domain input received signal
%
%   [Y,TFOUT] = HELPEROTFSDEMOD(X,M,PADLEN,SYMOFFSET,PADTYPE) performs
%   OTFS demodulation on X using a rectangular pulse shaping window and
%   outputs the results in Y. Specify X as a vector of real or complex
%   values. M is the number of subcarriers. The number of OTFS
%   subsymbols is inferred from the input size, PADTYPE, and PADLEN.
%   X - time-domain input including CP of size M*N+PADLEN if PADTYPE is
%   RCP or RZP, or of size (M+PADLEN)*N if PADTYPE is CP or ZP
%   M - number of subcarriers
%   PADLEN - CP or ZP length (in samples)
%   OFFSET - sample offset from beginning/end of OTFS symbol/subsymbol
%   PADTYPE (optional)
%     'CP'   = cyclic prefix (default)
%     'RCP'  = reduced cyclic prefix
%     'ZP'   = zero padding
%     'RZP'  = reduced zero padding
%     'NONE' = no CP/ZP
%   Y - DD domain output of size M-by-N
%   TFOUT - TF domain output produced during the two-step OTFS
%   demodulation of size M-by-N
%
%   See also helperOTFSmod and OTFSModulationExample.mlx.

%   Copyright 2023-2024 The MathWorks, Inc.

    if isempty(varargin)
        padtype = 'CP';
    else
        padtype = varargin{1};
    end

    % Remove CP and form delay-Doppler grid
    if strcmp(padtype,'CP') || strcmp(padtype,'ZP')
        % Full CP (offset = padlen) or Zero Padding (offset = 0)
        N = size(x,1)/(M+padlen);
        assert((N - round(N)) < sqrt(eps)); % check that M*N is an integer
        
        rx = reshape(x,M+padlen,N);
        Y = rx(1+offset:M+offset,:); % remove CPs
    elseif strcmp(padtype,'NONE')
        N = size(x,1)/M;
        assert((N - round(N)) < sqrt(eps)); % check that M*N is an integer
        
        Y = reshape(x,M,N);
    elseif strcmp(padtype,'RCP') || strcmp(padtype,'RZP')
        % Reduced CP (offset = padlen) or Reduced ZP (offset = 0)
        N = (size(x,1)-padlen)/M;
        assert((N - round(N)) < sqrt(eps)); % check that M*N is an integer

        rx = x(1+offset:M*N+offset); % remove CP
        Y = reshape(rx,M,N);
    else
        error('Invalid pad type');
    end

    % This code segment shows the SFFT/OFDM demod representation
    % Wigner transform with rectangular window (OFDM demodulator)
    tfout = fft(Y);

    % This code segment shows the simpler Zak transform representation
    y = fft(Y.').' * M;
end

注意函数里的这句话：% Reduced CP (offset = padlen) or Reduced ZP (offset = 0)，当前缀的类型设置为CP时，要使得参数offset的值核padlen一致，否则跑不起来。

3.6、多普勒信道响应

OTFS解调信号的输出是在（1,16）处传输的导频信号与DD域（5，-10）和（8,6）中的信道表示的卷积。这与OFDM解调不同，在OFDM解调中，OFDM解调信号是OFDM符号与频域信道系数的哈达玛（逐元素）乘积。

线性最小均方误差（LMMSE）估计器是一种使观测值Y（接收信号）和实际值P（已知导频信号）之间的均方误差最小化的估计方法，其给出如下：

其中P*是P的复共轭，σ2n是噪声功率。为了在延迟多普勒域中估计信道响应，在每个网格元素Ydd[k,l]上对单个导频符号Pdd使用LMMSE，并计算信道响应Hdd:

%用线性最小均方误差[linear minimum mean square error (LMMSE)]估计信道
Hdd = Ydd * conj(Pdd(1,pilotBin)) / (abs(Pdd(1,pilotBin))^2 + no);

用网格图可视化接收到的DD网格:

%信道响应三维图
figure;
xa = 0:1:N-1;
ya = 0:1:M-1;
mesh(xa,ya,abs(Hdd));
% view([-26.441 62.412]);
title('Delay-Doppler Channel Response H_{dd} from Channel Sounding');
xlabel('Normalized Doppler');
ylabel('Normalized Delay');
zlabel('Magnitude');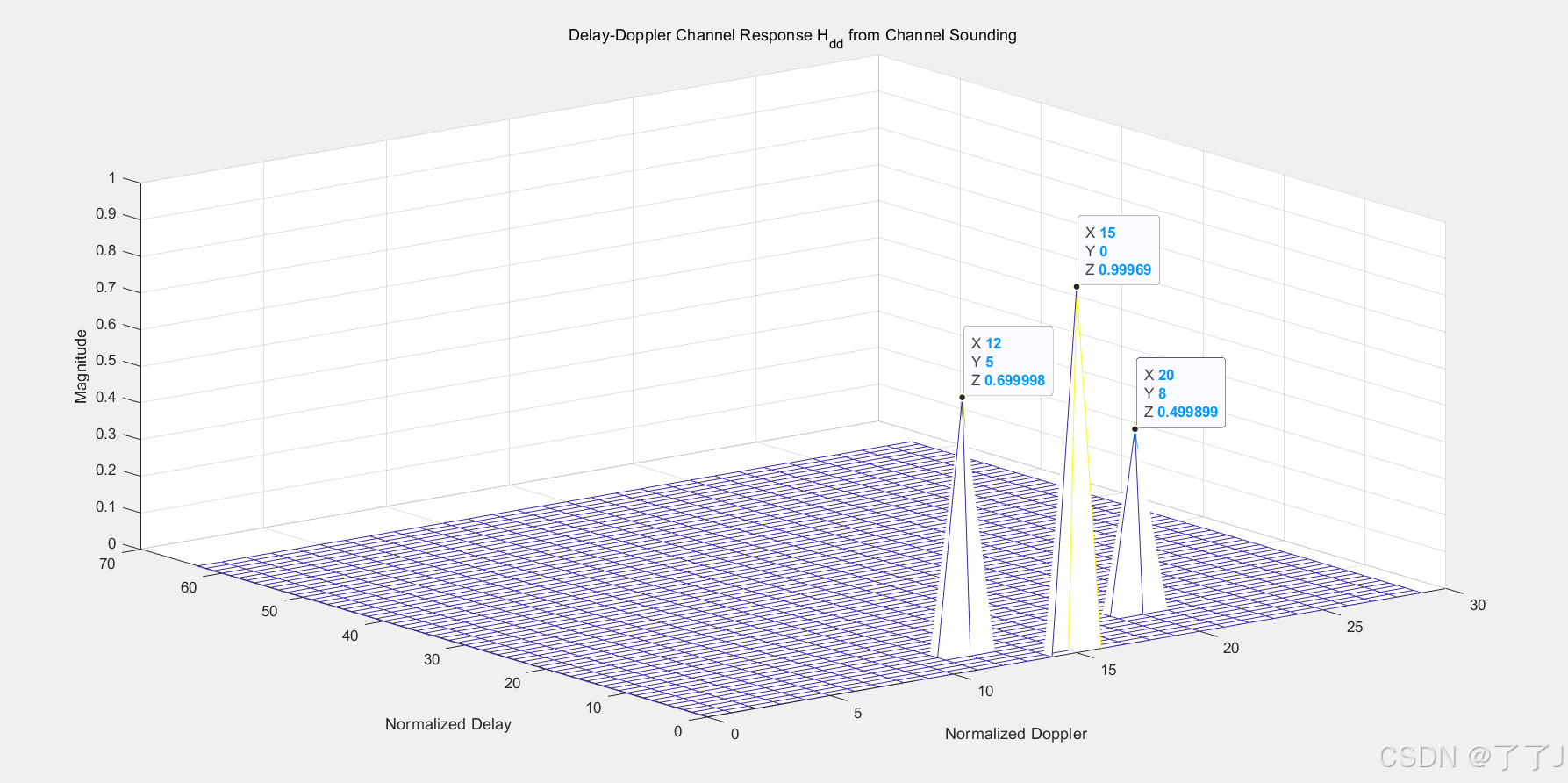

信道探测的DD网格显示了接收机从单个导频看到的所有路径、每条路径的延迟、每条路径上的多普勒频移和每条路径的复增益。观察导频符号如何在延迟多普勒域中与DD信道响应卷积。导频在正确的网格位置（1,16）被正确接收。另外两个散射体也出现在DD网格中。

.散射体1位于网格位置（1,16）+（5，-3）=（6,13）

.散射器2位于网格位置（1,16）+（8,5）=（9,21）

3.7、信道估计

延迟多普勒域中的信道估计需要估计信道响应中所有散射体的参数（延迟、多普勒和复增益）。从信道响应Hdd中，找到超过预设增益阈值的路径，并存储每个唯一路径的参数。存储信道估计值，以便以后在同一信道上传输数据时使用：

%通过Hdd找到信道中的时延与多普勒并映射到DD网格中
[lp,vp]=find(abs(Hdd)>=0.05);           %找出Hdd中幅值较大的点
chanEst.pathGains=diag(Hdd(lp,vp));     %信道增益
chanEst.pathDelays=lp-1;                %归一化时延
chanEst.pathDopplers=vp-pilotBin;       %归一化多普勒频谱

得到的增益，延迟与多普勒频偏的值与信道参数设置值一致，说明使用LMMSE进行信道估计效果非常好。

四、OFDM和OTFS在高移动性信道中的对比

OTFS和OFDM都通过循环前缀来抵消ISI的影响。然而，OFDM接收机中通常使用的单抽头频域均衡器（FDE）无法消除不同路径的多普勒频移对ICI的影响。在本节中，形成QPSK映射符号的M×N网格，并令OFDM和OTFS在高移动性信道上进行传输，以比较性能。

生成用于传输的数据：

%数据产生
Xgrid=zeros(M,N);
Xdata=randi([0,1],2*M,N);
Xgrid(1:M,:)=pskmod(Xdata,4,pi/4,InputType="bit");

4.1、OFDM经过高多普勒信道

在OFDM中，通过传输已知符号（导频）并在接收机处测量导频的失真来估计信道。通过在所有N个符号的所有M个子载波上传输导频来估计信道：

txout1=ofdmmod(exp(1i*pi/4)*ones(M,N),M,padLen);            %传输导频，全都是导频
dopplerOut1=dopplerChannel(txout1,fsamp,chanParams);        %经过时延多普勒信道
chOut1=awgn(dopplerOut1,SNRDB,"measured");                  %添加噪声
Yofdm=ofdmdemod(chOut1(1:(M+padLen)*N),M,padLen);           %解调
Hofdm=Yofdm*conj(Pdd(1,pilotBin))/(abs(Pdd(1,pilotBin))^2+no);    %LMMSE信道估计

由于导频信息都是已知的信号()，对接收到的信号Yofdm中的每一个点使用LMMSE便可得到估计的信道响应Hofdm。

使用OFDM传输数据网格。使用上述估计得到的信道响应Hofdm，在所有符号上使用单抽头FDE进行均衡：

txout2=ofdmmod(Xgrid,M,padLen);                           %调制
dopplerOut2 = dopplerChannel(txout2,fsamp,chanParams);    %经过时延多普勒信道
chOut2 = awgn(dopplerOut2,SNRDB,'measured');              %添加噪声
rxWindow = chOut2(1:(M+padLen)*N);                        %窗函数用于截取信号
Yofdm1 = ofdmdemod(rxWindow,M,padLen);                    %解调
Xhat_ofdm = conj(Hofdm) .* Yofdm1 ./ (abs(Hofdm).^2+no);  %用LMMSE进行均衡

用估计得到的信道响应Hofdm对接收信号Yofdm1上每一个点进行均衡，补偿经过信道后的损耗。

显示接收到的星座图并打印误码率。可以看到，即使具有高信噪比，星座图也会有噪声。

constDiagOFDM = comm.ConstellationDiagram( ...
    'ReferenceConstellation',pskmod(0:3,4,pi/4), ...
    'XLimits',[-2 2], ...
    'YLimits',[-2 2], ...
    'Title','OFDM with Single-Tap FDE');
constDiagOFDM(Xhat_ofdm(:));


XhatDataOFDM = pskdemod(Xhat_ofdm,4,pi/4, ...
    OutputType="bit",OutputDataType="logical");         % 解码
[~,berOFDM] = biterr(Xdata,XhatDataOFDM);
fprintf('OFDM BER with single-tap equalizer = %3.3e\n', berOFDM);

误码率结果为：OFDM BER with single-tap equalizer = 1.745e-02

将另外两个散射体的多普勒频移设置为零，在显示星座图并打印误码率：

误码率结果为：OFDM BER with single-tap equalizer = 0.000e+00

可以观察到即使噪声很小，BER也很高。虽然循环前缀可以减轻ISI，但时频域中的单抽头均衡无法补偿由多普勒频移路径引起的ICI，从而导致了BER的增加。

4.2、OTFS经过高多普勒信道

使用OTFS调制传输一样的数据网格：

%OTFS
txout3=helperOTFSmod(Xgrid,padLen,padType);                %OTFS调制
dopplerOut3 = dopplerChannel(txout3,fsamp,chanParams);     %经过多普勒信道
chOut3 = awgn(dopplerOut3,SNRDB,'measured');               %添加噪声

通用信号模型为y=Gx+n，其中x和y分别是传输到信道中的长度为MN的时域信号和从时域信道矩阵G接收的信号。如果已知G，则可以使用LMMSE来均衡信道。在矩阵形式中，LMMSE表示为：

通过时域均衡，可以使用单个路径的延迟和多普勒频移信息来消除ICI。根据之前发现的延迟多普勒信道参数估计形成信道矩阵:

% Form G matrix using channel estimates
G = getG(M,N,chanEst,padLen,padType);


function G = getG(M,N,chanParams,padLen,padType)
    % Form time domain channel matrix from detected DD paths
    if strcmp(padType,'ZP') || strcmp(padType,'CP')
        Meff = M + padLen;  % account for subsymbol pad length in forming channel
        lmax = padLen;      % max delay
    else
        Meff = M;
        lmax = max(chanParams.pathDelays);  % max delay
    end
    MN = Meff*N;
    P = length(chanParams.pathDelays);  % number of paths
    
    % Form an array of channel responses for each path
    g = zeros(lmax+1,MN);
    for p = 1:P
        gp = chanParams.pathGains(p);
        lp = chanParams.pathDelays(p);
        vp = chanParams.pathDopplers(p); 

        % For each DD path, compute the channel response.
        % Each path is a complex sinusoid at the Doppler frequency (kp)
        % shifted by a delay (lp) and scaled by the path gain (gp)
        g(lp+1,:) = g(lp+1,:) + gp*exp(1i*2*pi/MN * vp*((0:MN-1)-lp));
    end    

    % Form the MN-by-MN channel matrix G
    G = zeros(MN,MN);
    % Each DD path is a diagonal in G offset by its path delay l
    for l = unique(chanParams.pathDelays).'
        G = G + diag(g(l+1,l+1:end),-l);
    end
end

在延迟多普勒域中使用LMMSE对接收到的数据进行均衡和检测。假设噪声功率是已知的。

rxWindow = chOut3(1:numSamps);
y_otfs = ((G'*G)+no*eye(Meff*N)) \ (G'*rxWindow); % LMMSE
Xhat_otfs = helperOTFSdemod(y_otfs,M,padLen,0,padType); % OTFS demodulation

显示星座图并打印误码率：

constDiagOTFS = comm.ConstellationDiagram( ...
    'ReferenceConstellation',pskmod(0:3,4,pi/4), ...
    'XLimits',[-2 2], ...
    'YLimits',[-2 2], ...
    'Title','OTFS with Time-Domain LMMSE Equalization');
constDiagOTFS(Xhat_otfs(:));

XhatDataOTFS = pskdemod(Xhat_otfs,4,pi/4,OutputType="bit",OutputDataType="logical");
[~,berOTFS] = biterr(Xdata,XhatDataOTFS);
fprintf('OTFS BER with LMMSE equalization = %3.3e\n', berOTFS);

误码率结果为：OTFS BER with LMMSE equalization = 0.000e+00

可以看到，接收到的星座图比OFDM星座图更清晰，说明对于高多普勒信道环境，OTFS抗干扰能力大大优于OFDM。

五、总结

OTFS是一种有前景的调制方案，可以抵消移动环境中高多普勒的影响。本示例介绍了延迟多普勒域的概念、移动信道对该域中传输符号的影响以及如何调制和解调OTFS符号。使用OTFS和OFDM在同一信道上传输相同的数据，并在简单的信道估计和均衡后观察它们的BER，表明OTFS有效地对抗了ICI，而OFDM则不能。

文献中提供了更精确的信道估计和更有效的数据检测方法。该示例使用简单的信道估计技术和直接的信道均衡方法来展示OTFS在高多普勒信道中优于OFDM的优点。

六、参考文献

1. R. Hadani et al. "Orthogonal Time Frequency Space Modulation." 2017 IEEE Wireless Communications and Networking Conference (WCNC). San Francisco, CA, USA, 2017, pp. 1-6.

2. 3GPP TSG RA WG1. OTFS modulation waveform and reference signals for new RAT: Meeting #84-bis R1-162930. Busan, South Korea: 3GPP, 2016.

3. TSDSI. “6G Use Cases and Enabling Technologies.” Oct. 2022.

4. Y. Hong, T. Thaj, and E. Viterbo. Delay-Doppler Communications. London, Elsevier 2022.