《算法设计与分析》第二章：递归

已于 2024-06-01 22:10:53 修改
阅读量1k 收藏 30
点赞数 28
文章标签： 算法
于 2024-05-19 20:06:54 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_75027857/article/details/139026905
版权

文章目录

2.1 关于递归

2.1.1 递归的定义

  • 在定义一个过程或函数时出现调用本过程或本函数的成分，称之为递归。
  • 若调用自身，称之为直接递归。
  • 若过程或函数p调用过程或函数q，而q又调用p，称之为间接递归。
  • 任何间接递归都可以等价地转换为直接递归。
  • 如果一个递归过程或递归函数中递归调用语句是最后一条执行语
    句，则称这种递归调用为尾递归。

例：
在这里插入图片描述

int fun(int n)
{
  if(n==1)
    return (1);
  else
   return(fun(n-1)*n);
  }

在该函数fun(n)求解过程中，直接调用fun(n-1)（语句4）自身，所以它是一个直接递归函数。又由于递归调用是最后一条语句，所以它又属于尾递归。

2.1.2 何时使用递归

在以下三种情况下，常常要用到递归的方法。

  • 定义是递归的
  • 数据结构是递归的
  • 问题的求解方法是递归的

定义是递归的

有许多数学公式、数列等的定义是递归的。例如，求n!
和Fibonacci数列等。这些问题的求解过程可以将其递归定
义直接转化为对应的递归算法。
例如：
在这里插入图片描述

数据结构是递归的

有些数据结构是递归的。例如单链表就是一种递归数据结构，其
结点类型声明如下：

typedef struct LNode 
{ ElemType data;
 struct LNode *next; 
} LinkLis;

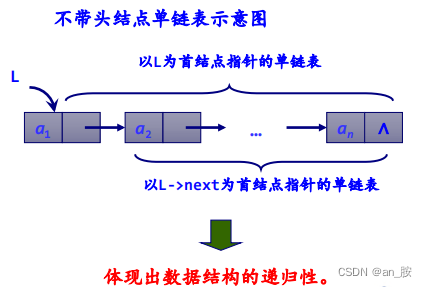
在这里插入图片描述

结构体LNode的定义中用到了它自身，即指针域next是一种指向自身类型的指针，所以它是一种递归数据结构。

例如:

  • 求一个不带头结点的单链表L的所有data域（假设为int型）之和的递归
    算法如下：
int Sum(LinkList *L)
{ if (L==NULL)
　　　　return 0;
　　else 
　　　　return(L->data+Sum(L->next));
}
  • 分析二叉树的二叉链存储结构的递归性，设计求非空二
    叉链bt中所有结点值之和的递归算法，假设二叉链的data域为int型。
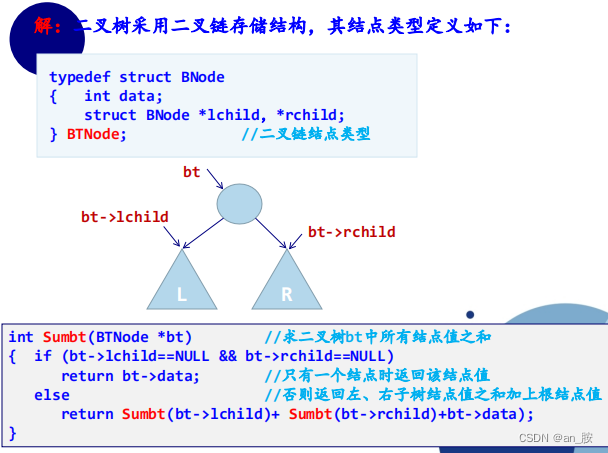
    在这里插入图片描述

问题求解方法是递归的

汉诺塔（Hanoi）问题求解

在这里插入图片描述
三阶汉诺塔问题解题步骤
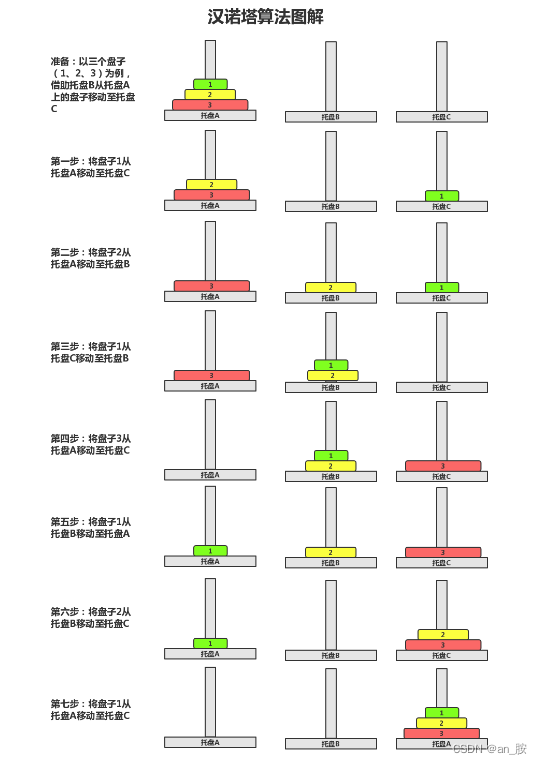
在这里插入图片描述

问题解法：

当n=1时，只要将编号为1的圆盘从柱子A直接移到柱子C上即可。
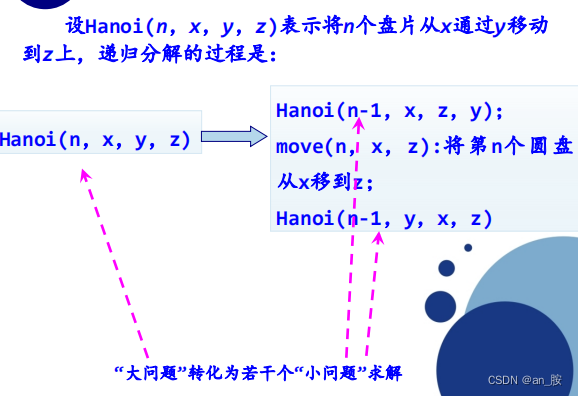
当n>1时，就需要借助另外一根柱子来移动。将n个圆盘由A移到C上可以分解为以下几个步骤：

(1)  将A柱子上的n-1个圆盘借助C柱子移到B柱子上;

(2)  把A柱子上剩下的一个圆盘从A柱子移到C柱子上;

(3)  最后将剩下的n-1个圆盘借助A柱子从B柱子移到C柱子上。

在这里插入图片描述

#include <stdio.h>

void move(int numberOfDisks, char start, char destination) {
    printf("将 %d 号盘子从 %c 柱移到 %c 柱\n", numberOfDisks, start, destination);
}

void hanoi(int numberOfDisks, char start, char spare, char destination) {
    if (numberOfDisks == 1) {
        move(1, start, destination);
        return;
    }
    hanoi(numberOfDisks - 1, start, destination, spare);
    move(numberOfDisks, start, destination);
    hanoi(numberOfDisks - 1, spare, start, destination);
}

int main() {
    int numberOfDisks;
    printf("请输入盘子数量: ");
    scanf("%d", &numberOfDisks);
    hanoi(numberOfDisks, 'A', 'B', 'C');
    return 0;
}

在这里插入图片描述
hanoi 函数的实现:

  • 如果只有一个盘子需要移动,直接调用 move 函数打印移动步骤即可。
  • 如果有多个盘子,则先将上面的 numberOfDisks - 1 个盘子从 start 移动到 spare柱子上,然后将最大的盘子从 start 移动到 destination柱子上,最后再将 spare 柱子上的 numberOfDisks - 1 个盘子移动到 destination 柱子上。这就是汉诺塔问题的典型递归解法。

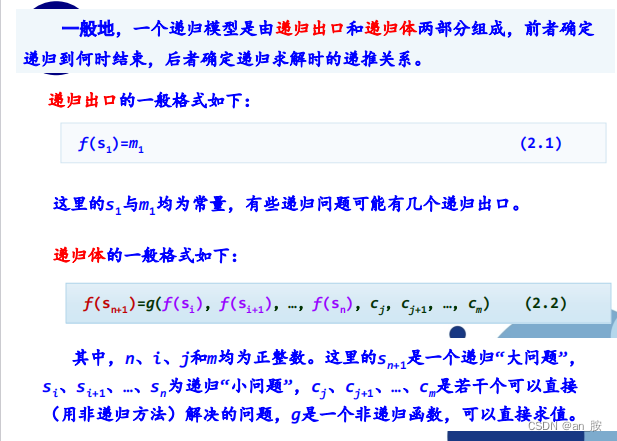
2.1.3 递归模型

递归模型是递归算法的抽象，它反映一个递归问题的递归结构。
在这里插入图片描述
在这里插入图片描述

2.1.4 递归算法的执行过程

  • 一个正确的递归程序虽然每次调用的是相同的子程序，但它的参量、输入数据等均有变化。
  • 在正常的情况下，随着调用的不断深入，必定会出现调用到某一层的函数时，不再执行递归调用而终止函数的执行，遇到递归出口便是这种情况。
  • 系统为每一次调用开辟一组存储单元，用来存放本次调用的返回
    地址以及被中断的函数的参量值。
    - 这些单元以系统栈的形式存放，每调用一次进栈一次，当返回时
  • 执行出栈操作，把当前栈顶保留的值送回相应的参量中进行恢复，并按栈顶中的返回地址，从断点继续执行。
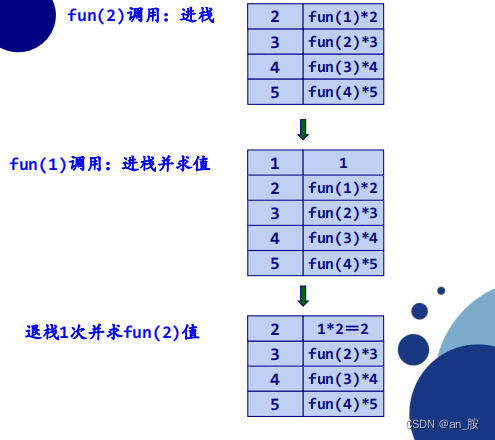
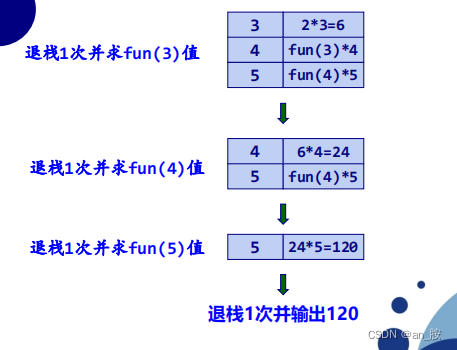
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

递归调用的实现是分两步进行:

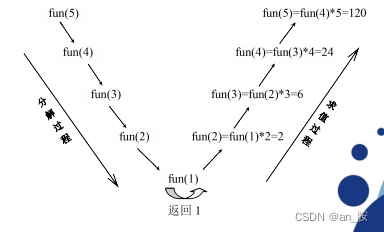
  1. 第一步是分解过程，即用递归体将“大问题”分解成“小问题”，直到
    递归出口为止；
  2. 第二步的求值过程，即已知“小问题”，计算“大问题”。前面的
    fun(5)求解过程如下所示。
    在这里插入图片描述

2.2 递归算法设计

2.2.1 递归算法设计的一般步骤

  1. 先找出 递归模型
  2. 转换为对应的C/C++语言函数
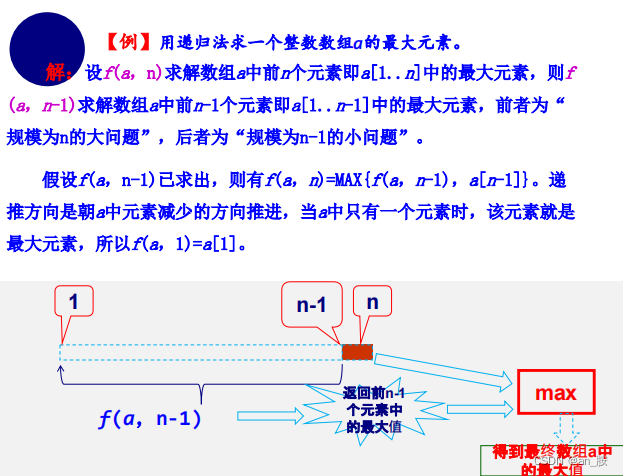
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
#include <stdio.h>
#include <stdlib.h>

int fmax(int a[], int n) {
    if (n == 1) {
        return a[0];
    } else {
        return max(a[n-1], fmax(a, n-1));
    }
}

int main() {
    int arr[] = {5, 2, 8, 1, 9, 3};
    int size = sizeof(arr) / sizeof(arr[0]);
    int max = fmax(arr, size);
    printf("The maximum element is: %d\n", max);
    return 0;
}

在这里插入图片描述

#include <stdio.h>

int Max(int A[], int i, int j) {
    if (i == j) {
        return A[i];
    } else {
        int mid = (i + j) / 2;
        int max1 = Max(A, i, mid);
        int max2 = Max(A, mid + 1, j);
        return (max1 > max2) ? max1 : max2;
    }
}

int main() {
    int arr[] = {5, 2, 8, 1, 9, 3};
    int size = sizeof(arr) / sizeof(arr[0]);
    int max = Max(arr, 0, size - 1);
    printf("The maximum element is: %d\n", max);
    return 0;
}

2.2.2 递归数据结构及其递归算法设计

1. 递归数据结构的定义
采用递归方式定义的数据结构称为递归数据结构。

在递归数据结构定义中包含的递归运算称为基本递归运算。

2. 基于递归数据结构的递归算法设计

  • 1）单链表的递归算法设计

【例1】有一个不带头结点的单链表L，设计一个算法释放其中所有结点。
在这里插入图片描述
【例2】设L为不带头结点的单链表，实现从尾到头反向输出链表中
每个结点的值。
在这里插入图片描述

2）二叉树的递归算法设计

【例】对于含n（n>0）个结点的二叉树，所有结点值为int
类型，设计一个算法由其先序序列a和中序序列b创建对应的二叉
链存储结构。
在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>

typedef char ElemType;
typedef struct BTNode {
    ElemType data;
    struct BTNode *lchild, *rchild;
} BTNode;

BTNode *CreateBTree(ElemType pre[], ElemType in[], int n) {
    int k;
    if (n <= 0) return NULL;
    ElemType root = pre[0]; // 根结点值
    BTNode *bt = (BTNode *)malloc(sizeof(BTNode));
    bt->data = root;
    for (k = 0; k < n; k++) // 在in中查找in[k]=root的根结点
        if (in[k] == root)
            break;
    bt->lchild = CreateBTree(pre + 1, in, k); // 递归创建左子树
    bt->rchild = CreateBTree(pre + k + 1, in + k + 1, n - k - 1); // 递归创建右子树
    return bt;
}

int main() {
    ElemType pre[] = {'A', 'B', 'D', 'E', 'C', 'F'};
    ElemType in[] = {'D', 'B', 'E', 'A', 'F', 'C'};
    BTNode *root = CreateBTree(pre, in, 6);
    // 您可以在这里添加遍历二叉树的代码进行测试
    return 0;
}

2.3 递归算法设计示例

青蛙跳台阶

问题描述：
青蛙跳台阶问题：一只青蛙一次可以跳上1级台阶，也可以
跳上2级。编写代码求青蛙跳上一个n级的台阶，总共有多少
种跳法？

思路：
如果青蛙第一次跳 1 级台阶,那么剩下 n-1 级台阶的跳法数为 f(n-1);
如果青蛙第一次跳 2 级台阶,那么剩下 n-2 级台阶的跳法数为 f(n-2);
所以 f(n) = f(n-1) + f(n-2)。

#include <stdio.h>

int frog_steps(int n) {
    if (n == 1) {
        return 1;
    } else if (n == 2) {
        return 2;
    } else {
        return frog_steps(n - 1) + frog_steps(n - 2);
    }
}

int main() {
    int n;
    printf("Enter the number of steps for the frog: ");
    scanf("%d", &n);
    printf("The number of ways for the frog to climb %d steps is: %d\n", n, frog_steps(n));
    return 0;
}

这个函数使用递归的方式实现了动态规划的思想。我们可以看到,当 n 较大时,这个递归实现效率会较低,因为会有大量重复计算。

为了提高效率,我们可以使用一个数组来存储中间结果,这样就不需要重复计算了。使用一个数组 dp 来存储中间结果。dp[i] 表示青蛙跳上 i 级台阶的总跳法数。我们先初始化 dp[1] 和 dp[2],然后使用动态规划的方法计算出 dp[3] 到 dp[n]。最后返回 dp[n] 作为最终结果。

下面是改进后的代码:

#include <stdio.h>

int frog_steps(int n) {
    int dp[n + 1];
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

int main() {
    int n;
    printf("Enter the number of steps for the frog: ");
    scanf("%d", &n);
    printf("The number of ways for the frog to climb %d steps is: %d\n", n, frog_steps(n));
    return 0;
}

瓷砖覆盖问题

问题描述：
编写代码求用2╳1小矩形横着或竖着去覆盖2╳n的大矩形。输
出总共有多少种覆盖方法。
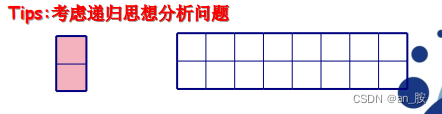
在这里插入图片描述
分析：

  • 我们先把2xn的覆盖方法记为f(n)。
  • 用第一个1x2小矩阵覆盖大矩形的最左边时有两个选择，竖着放或者横着放。
  • 当竖着放的时候，右边还剩下2x(n-1)的区域，这种情况下的覆盖方法记为f(n-1)。
  • 横着放的时候。当1x2的小矩形横着放在左上角的时候，左下角也必须横着放一个1x2的小矩形，而在右边还剩下2x(n-2)的区域，这种情况下的覆盖方法记为f(n-2)。
#include <stdio.h>

int cover_rectangle(int n) {
    if (n == 1) {
        return 1;
    } else if (n == 2) {
        return 2;
    } else {
        return cover_rectangle(n - 1) + cover_rectangle(n - 2);
    }
}

int main() {
    int n;
    printf("Enter the width of the rectangle: ");
    scanf("%d", &n);
    printf("The number of ways to cover the %d x 2 rectangle is: %d\n", n, cover_rectangle(n));
    return 0;
}

改进，使用数组记录数据，提高效率

#include <stdio.h>

int cover_rectangle(int n) {
    int dp[n + 1];
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

int main() {
    int n;
    printf("Enter the width of the rectangle: ");
    scanf("%d", &n);
    printf("The number of ways to cover the %d x 2 rectangle is: %d\n", n, cover_rectangle(n));
    return 0;
}

全排列问题

#include <stdio.h>
#include <stdlib.h>

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void Perm(int list[], int k, int m) {
    if (k == m) { // 找到一个完整的排列
        for (int i = 0; i <= m; i++) {
            printf("%d ", list[i]);
        }
        printf("\n");
    } else {
        for (int j = k; j <= m; j++) {
            swap(&list[k], &list[j]); // 交换第 k 个元素和第 j 个元素
            Perm(list, k + 1, m); // 递归处理剩余元素
            swap(&list[k], &list[j]); // 交换回原来的位置
        }
    }
}

int main() {
    int n;
    printf("请输入数组的长度: ");
    scanf("%d", &n);

    int list[n];
    printf("请输入数组元素: ");
    for (int i = 0; i < n; i++) {
        scanf("%d", &list[i]);
    }

    printf("全排列结果如下:\n");
    Perm(list, 0, n - 1);

    return 0;
}

Perm 函数:
这个函数实现了递归全排列的核心逻辑。
它有三个参数:
list: 要排列的数组
k: 当前要处理的起始索引
m: 数组的结束索引
首先,我们检查当前递归是否已经到达数组末尾(k == m)。如果是,则说明我们已经找到了一个完整的排列,输出结果。
如果还没有到达数组末尾,我们需要生成从 k 到 m 的所有可能排列:
我们遍历从 k 到 m 的所有元素。
对于每个元素 list[j],我们将其与 list[k] 交换,模拟将 list[j] 放在第 k 个位置。
然后递归调用 Perm(list, k+1, m),处理剩余的元素。
最后,我们再将 list[k] 与 list[j] 交换回去,保持数组的原始顺序,继续处理下一个元素。

整数划分问题

在这里插入图片描述
分析：以f（6,4）为例
在这里插入图片描述

正整数n的划分算法

#include <stdio.h>

int split(int n, int m) {
    if (n == 1 || m == 1) {
        return 1;
    } else if (n < m) {
        return split(n, n);
    } else if (n == m) {
        return split(n, n - 1) + 1;
    } else {
        return split(n, m - 1) + split(n - m, m);
    }
}

int main() {
    int n;
    printf("请输入一个正整数 n: ");
    scanf("%d", &n);

    int result = split(n, n);
    printf("正整数 %d 的划分数为: %d\n", n, result);

    return 0;
}

递归的简单选择排序

#include <stdio.h>

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void SelectSort(int a[], int i, int n) {
    int j, k;
    if (i == n) // 满足递归出口条件
        return;
    else {
        k = i; // k 记录 a[i..n] 中最小元素的下标
        for (j = i + 1; j <= n; j++) // 在 a[i..n] 中找最小元素
            if (a[j] < a[k])
                k = j;
        if (k != i) // 若最小元素不是 a[i]
            swap(&a[i], &a[k]); // a[i] 和 a[k] 交换
        SelectSort(a, i + 1, n); // 递归处理剩余元素
    }
}

int main() {
    int n, i;
    printf("请输入数组长度: ");
    scanf("%d", &n);
    int a[n];
    printf("请输入数组元素:\n");
    for (i = 1; i <= n; i++)
        scanf("%d", &a[i]);

    SelectSort(a, 1, n);

    printf("排序后的数组:\n");
    for (i = 1; i <= n; i++)
        printf("%d ", a[i]);
    printf("\n");

    return 0;
}

递归的冒泡排序

#include <stdio.h>
#include <stdbool.h>

void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void BubbleSort(int a[], int i, int n) {
    int j;
    bool exchange;
    if (i == n) // 满足递归出口条件
        return;
    else {
        exchange = false; // 置 exchange 为 false
        for (j = 1; j <= n - i; j++) {
            if (a[j] > a[j + 1]) { // 当相邻元素反序时
                swap(&a[j], &a[j + 1]);
                exchange = true; // 发生交换置 exchange 为 true
            }
        }
        if (exchange == false) // 未发生交换时直接返回
            return;
        else // 发生交换时继续递归调用
            BubbleSort(a, i + 1, n);
    }
}

int main() {
    int n, i;
    printf("请输入数组长度: ");
    scanf("%d", &n);
    int a[n + 1]; // 使用 1 作为数组起始下标
    printf("请输入数组元素:\n");
    for (i = 1; i <= n; i++)
        scanf("%d", &a[i]);

    BubbleSort(a, 1, n);

    printf("排序后的数组:\n");
    for (i = 1; i <= n; i++)
        printf("%d ", a[i]);
    printf("\n");

    return 0;
}

2.4 递归算法转化非递归算法

在这里插入图片描述

2.5 递归算法分析

当一个算法包含对自身的递归调用过程时，该算法的运行时间复
杂度可用递归方程进行描述，求解该递归方程，可得到对该算法
时间复杂度的函数度量。
在这里插入图片描述

递归方程求解

（1）替换法

替换方法的最简单方式为：根据递归规律，将递
归公式通过方程展开、反复代换子问题的规模变量，
通过多项式整理，如此类推，从而得到递归方程的解。
在这里插入图片描述

在这里插入图片描述
总结：
在这里插入图片描述

（2）用特征方程求解递归方程

在这里插入图片描述
在这里插入图片描述
特征方程的k个根不同：
在这里插入图片描述
特征方程k个根有重根
在这里插入图片描述

前面2种情况下的c1,c2,…,ck均为待定系数； 将初始条件代入，建立联立方程，确定各个系数具体值， 得到通解f(n)。

  • 例【1】：
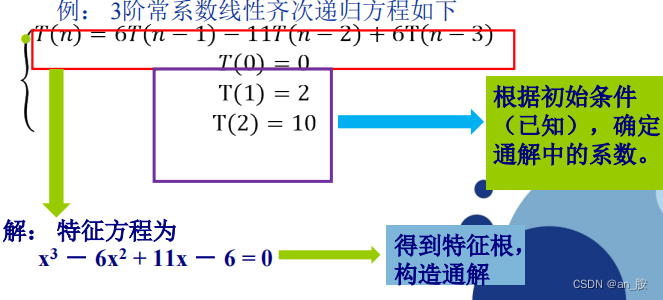
    在这里插入图片描述
    在这里插入图片描述
    ·
  • 例【2】：
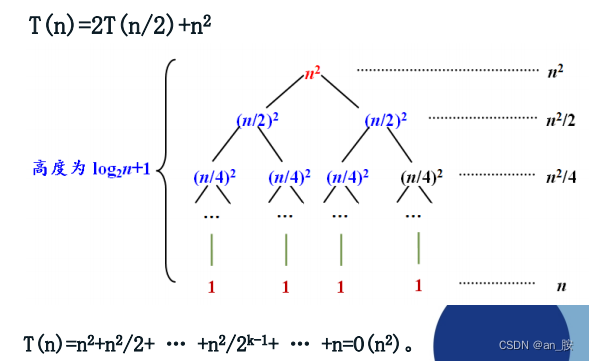
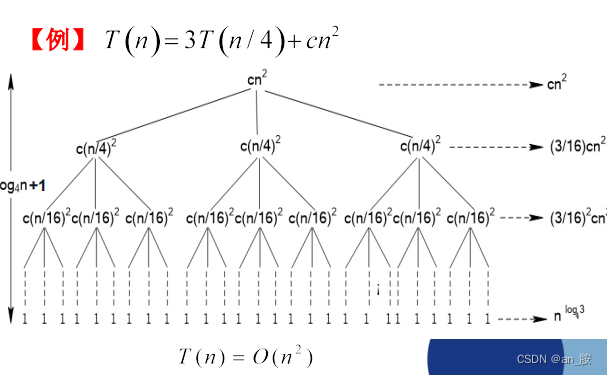
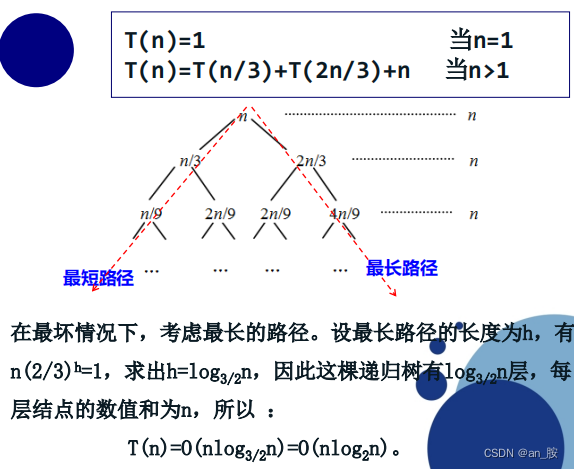
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

（3）递归树法

  • 用递归树求解递归方程的基本过程是：
    ① 展开递归方程，构造对应的递归树。
    ② 把每一层的时间进行求和，从而得到算法时间复
    杂度的估计
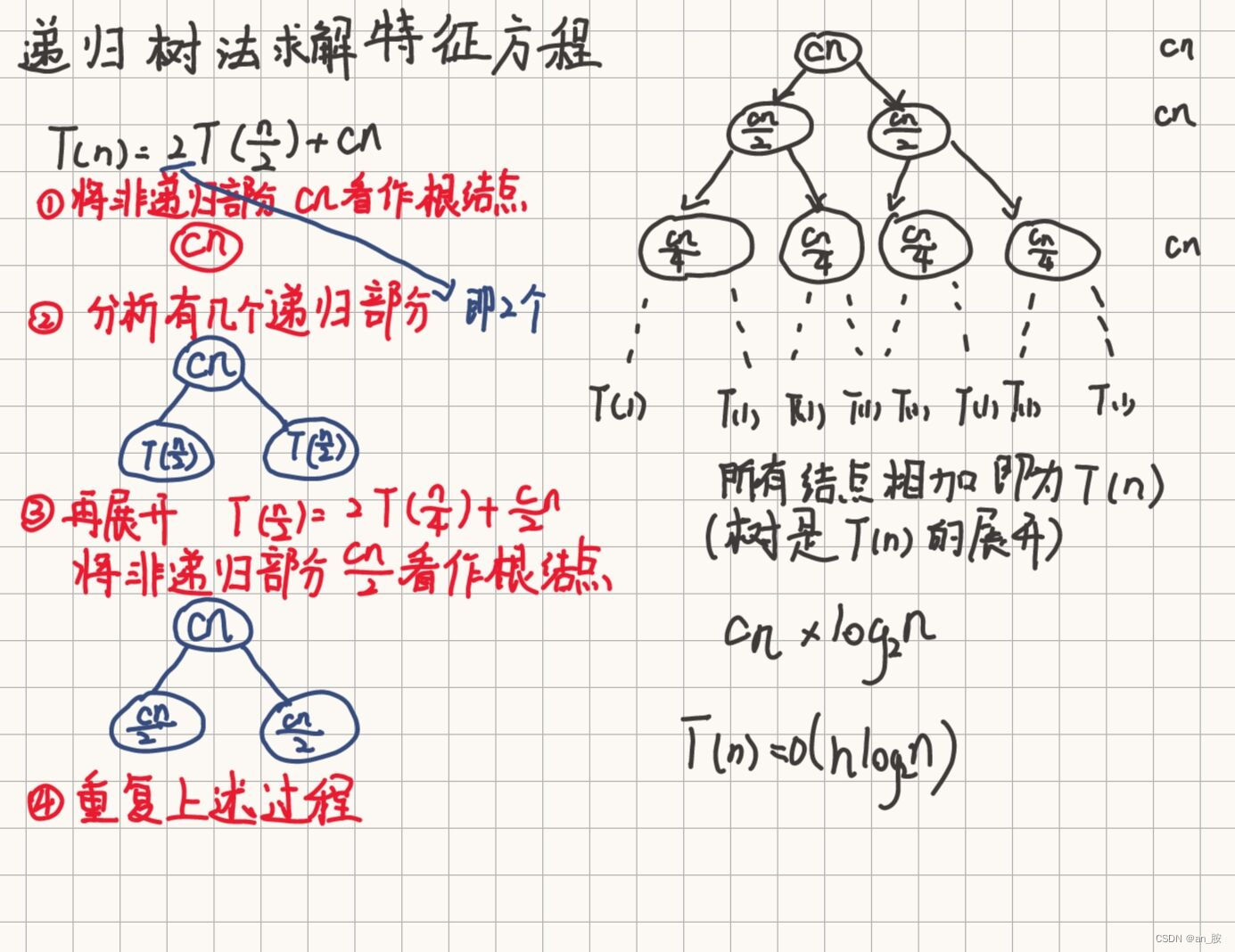
    在这里插入图片描述

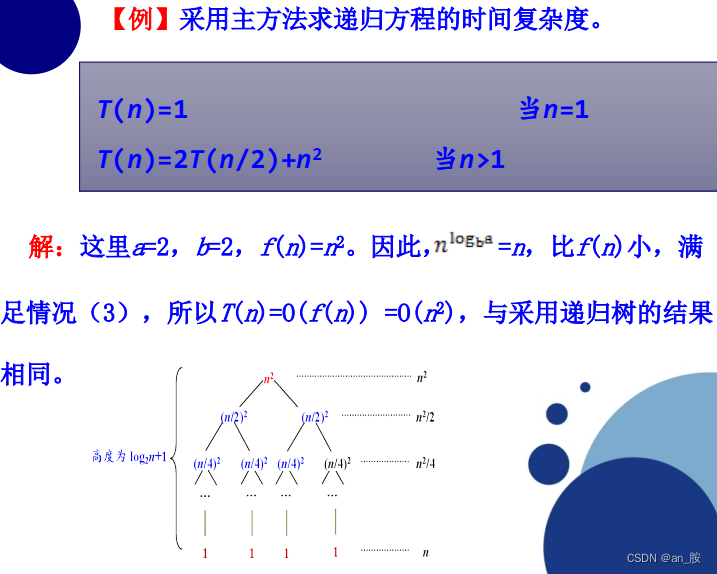
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
此处在这里插入图片描述

（4）主方法

在这里插入图片描述
应用方法：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

an_胺
关注
  • 28
    点赞
  • 踩
  • 30
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
算法设计与分析第四章1
08-03
【算法设计与分析第四章】主要探讨了动态规划这一重要的算法设计策略，通过解决一系列典型问题来阐述其原理和应用。动态规划是一种用于求解最优化问题的有效方法，它通过分解问题并存储中间结果，避免了重复计算，...
算法设计与分析第二章1
08-03
在算法设计与分析的学习中，第二章主要涵盖了算法分析的基础概念和理论，这些内容对于深入理解和评估算法效率至关重要。以下是对各个知识点的详细说明： 1. **大O符号与渐进行为**： - 大O记号表示算法运行时间的...
算法设计与分析第二章（递归算法） 课后习题答案（c++）
qq_46664080的博客
03-18 965
该文章是算法设计与分析（第二版）中各章的课后习题 主编 ： 李春葆 在本文中，主要是对该书第二章-递归算法设计技术章节中的在线编程题进行代码解答。 代码运行环境是：DEVc++
《算法设计与分析》第二章 递归与分治策略
Concise200的博客
01-18 1779
第二章 递归与分治策略1. 递归阶乘函数(O(n))Fibonacci数列（O(2^n)）排列问题Hanoi塔问题2.分治法二分搜索技术（O(logn)） 1. 递归 阶乘函数(O(n)) int factorial(int n) { if(n==0) return 1; return n*factorial(n-1); } Fibonacci数列（O(2^n)） int fibonacci(int n) { if(n<=1) return 1; return f
算法设计与分析第二章期末总结
聆风吟的博客
05-26 2369
本文主要总结一些常用的算法模板，适用于期末考试。
【精选】算法设计与分析（第二章递归算法设计技术）
VLOKL的博客
12-12 704
【精选】算法设计与分析（第二章递归算法设计技术）
算法设计与分析：第2章 递归法.pdf
09-17
算法设计与分析：第2章 递归法.pdf
算法设计与分析课后习题答案（c++）
06-02
算法设计与分析（第二版）中各章的课后习题 C++代码解答。主要是对 1 - 8章 以及 第10章中的课后习题进行代码解答，主要包括的章节有第1章概论、第2章递归算法设计技术、第3章分治法、第4章蛮力法、第5章回溯法、第6...
算法分析与设计第二章知识点以及思维导图
10-16
算法分析与设计第二章知识点以及思维导图 本章节主要介绍了递归与分治策略的概念和实例，旨在帮助读者理解和掌握递归和分治算法的设计和分析。 一、递归的概念 递归是指一个算法直接或间接地调用自身的函数，这种...
算法的学习笔记—删除链表中重复的结点（牛客JZ76）
最新发布
业精于勤，荒于嬉
08-14 779
本文介绍了一种删除排序链表中重复节点的高效算法。通过递归的方式，算法能够有效地删除所有重复节点，并保留链表中仅出现一次的节点。此方法的实现简单且易于理解，同时在时间和空间复杂度方面表现优异，适用于处理大规模数据链表中的重复节点问题。😁热门专栏推荐想学习vue的可以看看这个java基础合集数据库合集redis合集nginx合集linux合集手写机制微服务组件spring_尘觉springMVCmybits🤔欢迎大家加入我的社区尘觉社区。
【LeetCode每日一题】——623.在二叉树中增加一行
IronmanJay的博客
08-14 665
给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。 注意，根节点 root 位于深度 1 。 加法规则如下: 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。 cur 原来的左子树应该是新的左子树根的左子树。 cur 原来的右子树应该是新的右子树根的右子树。 如果 depth == 1 意味着 depth - 1 根本没有深度
代码随想录算法训练营第十一天
b1ankwall的博客
08-10 1242
参加代码随想录第43期算法训练营day11|150. 逆波兰表达式求值，239. 滑动窗口最大值，347.前 K 个高频元素，栈与队列总结
[算法2] 第二集 二叉树中的深度搜索
2301_80017277的博客
08-09 886
一、（DFS，全称为 Depth First Traversal），是我们树或者图这样的数据结构中常⽤的⼀种遍历算法。这个算法会尽可能深的搜索树或者图的分支，直到⼀条路径上的所有节点都被遍历完毕，然后再回溯到上⼀层，继续找⼀条路遍历。在⼆叉树中，常见的深度优先遍历为：前序遍历、中序遍历以及后序遍历。因为树的定义本⾝就是递归定义，因此采⽤递归的方法去实现树的三种遍历不仅容易理解⽽且代码很简洁。
算法：外卖调度
m0_73915763的博客
08-13 974
有N个餐厅和M个外卖员，每个餐厅在某个时间点会产生一个外卖订单，这些订单都有产生时间、所需送达时间和优先级。外卖员在空闲时会选择最优先的订单来配送，直到所有订单都被送达。具体规则如下: 对于每个餐厅的订单，优先级高的订单优先，其次是所需送达时间最短的订单，再次是产生时间最早的订单。外卖员在空闲时会从所有餐厅的最高优先级订单中挑选一个所需送达时间最短的订单进行配送，若所需送达时间相同则选择餐厅编号最小的订单。
【算法】二分查找
2301_80277275的博客
08-10 281
二分查找、在排序数组中查找元素的第一个和最后一个位置、x的平方根、搜索插入位置、山脉数组的峰顶索引、寻找峰值、寻找旋转排序数组中的最小值、点名
经典算法题总结：十大排序算法，外部排序和Google排序简介
技术研究记录
08-10 572
快速排序（Quick Sort）是一种常用的高效的排序算法，它是一种基于比较的排序算法，利用了分治（自顶向下）的思想。快速排序的主要思想是选择一个基准元素，将数组分成两个子数组，一个子数组的所有元素都小于基准元素，另一个子数组的所有元素都大于基准元素，然后递归地对这两个子数组进行排序，最后将它们合并起来。
浙大版《C语言程序设计（第3版）》题目集
qq_67330059的博客
08-09 382
其中a和b是用户传入的参数，函数返回的是两者中较大的数。
矩阵转置（c语言）
scy2429828663的博客
08-09 803
int m = 0;int a = 0;//输入 n m//将数据存储在arr上//输入 aj < n;j++)i < m;i++)//转置i < m;i++)j < n;
算法设计与分析：从递归到近似算法
第二章“递归与分治策略”讲解了递归的基本原理，递归是函数或过程调用自身的一种方法，通常用于解决复杂问题。分治策略是一种将大问题分解为小问题来解决的策略，它常与递归结合使用，例如在排序算法（如快速排序、...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值