Erlang排队系统

Erlang分布本身不就有无后效性，但K阶Erlang分布可看作K个相互独立、相同指数分布的随机变量之和的分布。因而，可以利用负指数分布的无后效性来分析Erlang排队系统。（M/Ek/1/∞和Ek/M/1/∞）

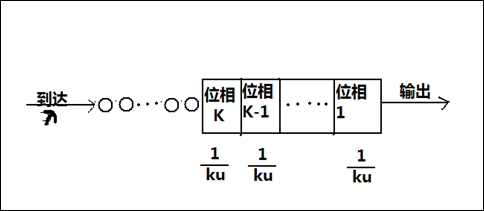
在M/Ek/1/∞系统中，把服务时间假想分为K个独立同分布的位相，一个顾客必须通过k个位相服务完成后才允许别的顾客进入服务。

 

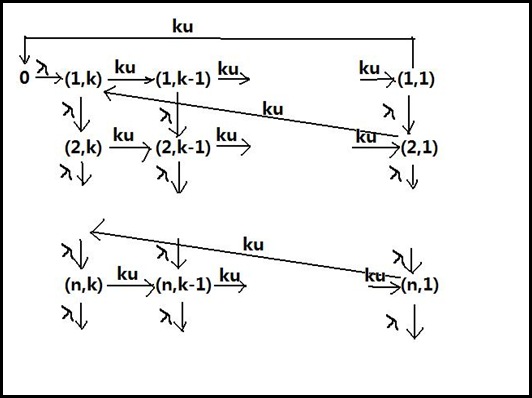
令N(t)为t时刻系统所处的状态，状态用二元组（n，j）表示，转移强度图为

根据转移强度图列出统计平衡下的差分方程，即可求解统计平衡下的平均队长、等待队长、平均等待时间和平均逗留时间。

对于Ek/M/1/∞系统，可用相似的办法来处理和计算。当然，计算过程比较复杂，需要一些技巧。