斐波那契数列

斐波那契数列又称“兔子数列”，因为这个数列可以用一个有关兔子的问题来描述：一对兔子在出生两个月后，每个月都可以生出一对小兔子，如果兔子能够长命百岁，那么１对兔子在第ｎ个月，会变成多少对兔子呢？

 第1、2个月，兔子都是1对，第3个月，第1对小兔子出生了，共2对……第n个月，比前一个月多出的小兔子总数就是两个月前（第n-2个月）的兔子总数。这样，兔子总数就构成了这样的一个数列：1,1,2,3,5,8,13…从第三项起，每一项都是前两项之和。

 这个问题是一个循环计算问题，从前两项的1,1起，循环计算最后两项的和来作为新项的值就可以。 在esProc中，可以通过下面的方法循环计算：

	A	B	C
1	20
2	/ for n Loop
3	=[1,1]
4	for A1-2	=A3.m(-1)+A3.m(-2)	>A3=A3|B4

这个方法是用for n循环来循环执行指定次数，由于在初始设定中已经设定了第一项和第二项的值，因此循环计算的次数也要减2。A3中存储斐波那契数列，B4中计算数列的最后两项之和，C4中的语句把B4中的结果添加到数列中。流程图如下：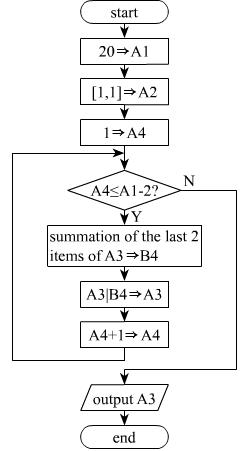

计算完成后，A3中的结果为：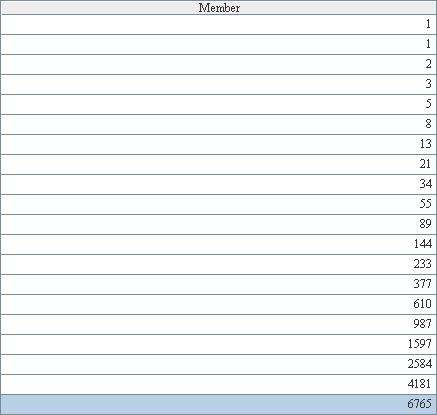

在esProc中，还可以选用for x循环，当x的值为true时一直循环执行语句块，如下图所示：

5	/while Loop
6	=[1,1]
7	for A6.len()<A1	>A6=A6|A6.m(-1)+A6.m(-2)

A6中存储斐波那契数列，根据A7中的语句，当项数小于指定总数时循环执行，B7中的语句相当于合并了B4和C4中的语句，直接计算出新项添加入数列。流程图如下：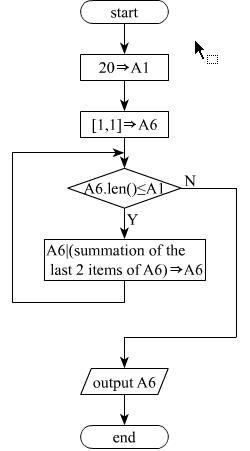

计算完成后，A6中的结果和A3中是相同的。
在esProc中，还可以不使用for循环语句，而使用循环函数来实现循环计算：

8	/n.(x)
9	>a>0,b=1
10	=A1.((b=a+b,a=b-a))

 A9中初始设定为第0项和第1项的值，在A10的循环函数中，每次计算出下一项的值赋值给b，并把原有的b值即当前项的值赋给a同时把数列的当前项设为a。使用循环参数，可以使代码量有效精简，流程图如下：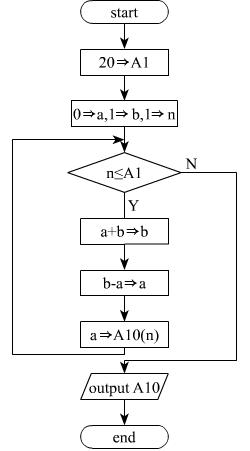

A10中的计算结果和A3是相同的。
还可以使用esProc中的子程序计算：

11	/fun
12	=func(A13,A1)
13	func	if A13<=2	return A13*[1]
14		=func(A13,A13-1)	return B14|B14.m(-1)+B14.m(-2)

A13格后面的子程序部分，使用递归计算指定项数的斐波那契数列。在子程序中，使用if语句判断，将斐波那契数列的产生划分为两种情况，当项数小于等于2时，直接在每一项中填1；如果项数大于2，在B14中通过递归调用函数获得前n-1项，再计算最后两项的和，把结果添加到数列中。A12中的计算结果和A3是相同的。

比较这几种计算方法，可以发现，for循环的思路简单，理解比较容易；循环函数的代码量最少；而子程序调用的使用比较方便，代码的复用率比较高，更适用于需要重复同种计算的时候。在应用中，可以根据需要做出选择.