挑战408——数据结构（6）——标准复杂类

合并算法的算法复杂度

上一篇，我们可以通过分治法实现了排序功能，现在我们来分析一下它的算法复杂度。按照以前的分析方式，调用合并排序算法来对一组含N个数的vector进行排序的时候，运行时间可以分为下面两个部分：

1. 执行非递归调用所需要的的时间。
2. 执行递归调用所需要的的时间。

我们先看非递归调用的时间，在递归调用sort函数之前，我们需要对N个vector中的数据进行分解，然后将分解的数据填充到两个小vector中，这个过程需要循环执行N轮。同样，合并填充的操作也跟当初分解填充是一样的。于是实际的非递归操作次数为 O（2N），忽略常数也就是O（N）。
那么递归调用所用的时间呢？要排序大小为N的vector，我们就必须递归排序大小为N / 2的两个vector。这些排序操作中的每一个都需要相同的时间。相同的逻辑，这些较小向量中的每一个进行排序需要与该级别的N / 2成正比，再加上其自身递归调用所需的时间，这个过程将一直持续到达到simple case（vector由单个元素组成或根本没有元素）。
解决问题所需的总时间就是每个级别中递归分解所需时间的总和。用回上篇的例子，这里分解一下递归分解的过程：

当我们向下递归分解时，vector虽然变小，但变得更多。但是，在每个层次上所做的工作总是与N成正比。因此，确定总工作量是一个发现有多少级别的问题。（即能分多少层就可以到达simple Case）。
上图可以看到，每一层的值都是上一层中的值除以所得，因此在vector大小被分到1之前，总层数 = N能被2除的次数，换成数学语言就是，找到这样的一个k，使得

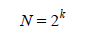
成立即可。显然：

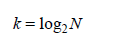
因为N可以分成k层，且每一层要完成的总操作数（执行次数）都是N，所以总的执行次数N log2N。对数通常以10（常用对数）或数学常数e（自然对数）的幂表示，但是与其他科学学科不同，计算机科学倾向于使用基于2的幂的二进制对数。因为使用不同的幂计算的对数 基数只有一个常数因子不同，因此在讨论计算复杂度时，我们通常省略对数基数。 因此，合并排序的计算复杂度通常写为：

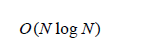
比较N^2 和N log2N的性能

但是O（N log N）有多好？ 我们查看一下实验数据，了解一下选择和合并排序算法的运行时间如何。 该时序信息如下图所示：

对于10个项目，合并排序的这种实现比选择排序慢五倍多。 在100个项目，选择排序仍然更快，但快的不是那么明显了。 当输入100,000个项目时，合并排序比选择排序快几百倍，选择排序算法需要两分半钟以上的时间来排序100,000个项目，而合并排序在不到半秒钟内完成作业。对于大型vector，合并排序显然是一个对大数据排序的显著的改进。
另外，我们还可以通过比较两种算法的计算复杂度公式获得相同的信息，如下所示：

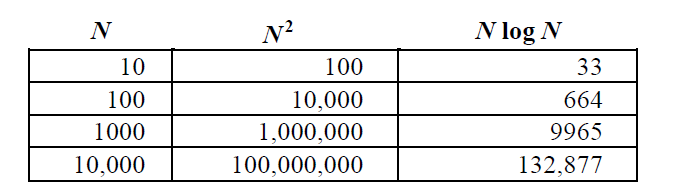
我们可以获得相同的信息： 随着N变大，两列中的数字都在增长，但N平方列的增长速度比N*log N列快得多。 因此，基于N log N算法的排序算法对于更大范围的vector是很有效果的。

标准复杂类

在编程中，大多数算法属于几种常见的复杂类。最重要的复杂性类别下表所示，它给出了类的通用名称以及相应的big-O表达式和该类中的代表性算法：

因为N的值会逐渐变大。下图显示了以对数刻度绘制的相同数据，可以更好地了解这些函数随着N增大时，复杂度的增长趋势：
当N很小的时候，

当N很大的时候：

属于常数，线性，二次和立方复杂度类以及其他更为一般的算法都是一般称为多项式算法（polynomial algorithms）。它们都在时间N的k次方中执行（k是常数）。从图中可以看出，随着N值的增加，函数N^k 无论k多大，都始终比 2的N次方涨的更慢。
这个属性在找到解决现实问题的实际算法方面具有重要的意义。比如选择排序示例清楚地表明，二次算法对于N的值变大也具有实质的解决方式（如我们的分开再合并），但是其复杂度为O（2^N）的算法都相当差。作为一般的经验法则，计算机科学家将可以通过多项式时间运算的算法解决的问题分类为易于解决的问题（intractable），因为它们可以在计算机上实现。没有多项式时间算法存在的问题都被认为是困难的（intractable）（比如2的N次方一类）。
然而，许多商业上重要的问题，所有已知算法都需要指数时间。比如我们学离散数学中，学习图的时候的邮递员问题（寻求找到一个可以通过一些交通系统连接的一组N个城市的最短路线，然后回到起点）。这些问题最有效的解决方案是尝试所有可能性，这当然需要指数时间。但是另一方面，没有人能够最终证明不存在这个问题的多项式时间算法。可能会有一些聪明的算法使这些问题易于处理。如果真的是这样，那么目前认为很困难的许多问题也将进入易处理的范围。
像邮递员这一类的问题，我们将它称为NP-完全问题（* NP-complete problems*），是否可以在多项式时间内解决问题是计算机科学中最重要的开放性问题之一，同样这也疏于数学领域的问题。