支持向量机（Supporting Vector Machine）SMO（Sequential Minimal Optimization）算法

reept

已于 2024-01-09 11:19:34 修改

阅读量436

点赞数 8

分类专栏：机器学习算法文章标签：算法支持向量机机器学习 svm

于 2023-12-24 10:08:46 首次发布

本文链接：https://blog.csdn.net/reept/article/details/134585955

版权

机器学习算法专栏收录该内容

8 篇文章 0 订阅

订阅专栏

一、算法提出的背景

SMO是一种支持向量机实现的算法，支持向量机的学习问题可以化为求解凸的二次规划问题。这样的凸二次规划问题，具有全局最优解，有许多优化算法可以用于这一问题的求解,但是当样本容量很大时，很多算法的时间复杂度和空间复杂度都会迅速增加，以致无法使用。因此高效实现SVM就成为一个重要的问题，SMO 就是在这样的背景下提出来的，这种算法由Platt 1998年提出。

二、算法的基本问题

如上所述，SMO要解决已经化为如下形式的凸二次规划的对偶问题：

$\underset{\alpha }{min}$ $\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha _{i}\alpha _{j}y_{i}y_{j}K(x_{i},x_{j}) - \sum_{i=1}^{N}\alpha _{i}$ -------------（1）

$s.t. \sum_{i=1}^{N} \alpha_{i}y_{i} =0$ -------------（2）

$0 \leqslant \alpha _{i} \leqslant C, i =1,2,3,...N$ -------------（3）

求解： $\alpha ^{*} = \left ( \alpha _{1}^{*}, \alpha _{2}^{*}......,\alpha _{N}^{*}\right )^{T}$

在该问题中，α 是拉格朗日乘子，一个变量 $\alpha ^{*}_{i}$ 对应一个样本点，变量的总数等于训练样本容量总数（由此也可知，SVM算法并不适合样本容量太多的数据集）。

拉格朗日乘子是上述问题的解充分必要条件是：满足KKT条件,即 $\alpha ^{}_{i}$ 取值在以下范围，并且满足相对应的检验（推导式右边）：

当 $\alpha _{i} = 0 \Rightarrow y_{i}g(x_{i}) \geqslant 1$

$0< \alpha _{i} < C \Rightarrow y_{i}g(x_{i}) = 1$

$\alpha _{i} = c \Rightarrow y_{i}g(x_{i}) \leqslant 1$

SMO算法的基本想法是：如果所有变量的解都满足此最优化问题的KKT条件，那么此时的所有变量就对应这个最优化问题的一个解。因为如上所述，KKT条件是该最优化问题的充分必要条件。否则，选择这些变量中的两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解。通过每次筛选两个变量，求解这个2变量规划问题，实现逐步接近问题最终解。

子问题有两个变量，一个是违反KKT条件最严重的那一个，另一个由约束条件自动确定。假设 $\alpha_{1}$ 、 $\alpha_{2}$ 为两个变量， $\alpha_{3}$ ， $\alpha_{4}$ 、 $\alpha_{5}$ ，......, $\alpha_{N}$ 固定，那么由等式（2）约束可知，

$\alpha _{1} = -y_{1}\sum_{i=2}^{N}\alpha _{i}y_{i}$

如果 $\alpha_{2}$ 确定，那么 $\alpha_{1}$ 也随之确定，所以问题同时更新两个变量。

三、两变量二次规划的求解方法

3.1 二次规划求解方法

对于上述，两变量二次规划，假设选择的变量是 $\alpha _{1}$ 、 $\alpha_{2}$ ,其他变量 $\alpha_{i}$ 是固定的。于是MSO的最优化问题可以写成下式：

$min \Psi (\alpha _{1}, \alpha _{2}) = \frac{1}{2}K_{11}\alpha ^{2}_{1} + \frac{1}{2}K_{22}\alpha ^{2}_{2} + y_{1}y_{2}K_{12}\alpha _{1}\alpha _{2} -(\alpha _{1}+ \alpha _{2}) + y_{1}\alpha _{1}\sum_{i=3}^{N}y_{i}\alpha_{i}K_{i1} + y_{2}\alpha_{2}\sum_{i=3}^{N}y_{i}\alpha_{i}K_{i2} + constant$ ----------（4）

s.t. $\alpha_{1}y_{1} + \alpha_{2}y_{2} = - \sum_{i=3}^{N}y_{i}\alpha_{i} = \zeta$ ----------（5）

$0 \leqslant \alpha_{i} \leqslant C, i = 1,2$ ----------（6）

其中， $K_{ij} = K(x_{i},x_{j}), i,j= 1,2,...,N, \zeta$ 是常数，目标函数式（4）省略了不含 $\alpha_{1}$ 、 $\alpha_{2}$ 的常数项。

不等式约束（6）使得 $(\alpha_{1},\alpha_{2})$ 在盒子[0,C] $\times$ [0,C] 内，等式约束（5）使得 $(\alpha_{1},\alpha_{2})$ 在平行于盒子对角线的直线上，因此求解问题的转为目标函数在平行于对角线的线段上的最优值。这样由约束条件可知，最优化问题变成了单变量的最优化问题，可以考虑为 $\alpha_{2}$ 的最优化问题。

假设（4）、（5）、（6）的初始可行解为 $\alpha ^{old}_{1}$ 、 $\alpha ^{old}_{2}$ 最优解为 $\alpha ^{new}_{1}$ 、 $\alpha ^{new}_{2}$ ,并且假设在沿着约束方向未经剪辑时 $\alpha_{2}$ 的最优解为 $\alpha ^{new ,unc}_{2}$ ， $\alpha ^{new}_{2}$ 必须满足（5）、（6）式约束，所以最优值 $\alpha ^{new}_{2}$ 满足：

$L \leqslant \alpha _{2}^{new} \leqslant H$

其中L 与H 是 $\alpha ^{new}_{2}$ 所在对角线端点的界。如果 $y_{1} \neq y_{2}$ (如下图所示），则

L =max(0, $\alpha ^{old}_{2}$ - $\alpha ^{old}_{1}$ ) , H = min(C,C + $\alpha ^{old}_{2}$ - $\alpha ^{old}_{1}$ ) --------------(7)

如果 $y_{1} = y_{2}$ ，则：

L =max(0, $\alpha ^{old}_{2}$ + $\alpha ^{old}_{1}$ -C) , H = min(C, $\alpha ^{old}_{2}$ + $\alpha ^{old}_{1}$ ) --------------(8)

图 3-1 二变量优化示意图

首先求沿着约束方向未经剪辑时的解，然后求经过剪辑的解（即考虑不等式（6））。

设 $g(x) = \sum_{i=1}^{N}\alpha _{i}y_{i} K(x_{i},x)+ b$ 令 $E_{i}$ = $g(x_{i}) - y_{i}$ = $\sum_{i=1}^{N}\alpha _{i}y_{i} K(x_{i},x)+ b -y_{i}$ i =1,2;

当 i =1,2时， $E_{i}$ 为函数 $g(x)$ 对输入 $x_{i}$ 的预测值与真实值之差。

由《统计学习方法》（李航，第二版）P145 定理7.6 可知:

优化问题（4）、（5）、（6）沿着约束方向未经剪辑时的解是：

$\alpha _{2}^{new,unc} =\alpha _{2}^{old} + \frac{y_{2}(E_{1}-E_{2})}{\eta }$ -----------(9)

其中， $\eta = K_{11} + K_{22} -2K_{12}$ = $\left \| \Phi (x_{1}) - \Phi (x_{2}) \right \|^{2}$ $E_{i}$ 为函数 $g(x)$ 对输入 $x_{i}$ 的预测值与真实值之差， $\Phi (x_{})$ 为输入空间到特征空间的映射。

经过剪辑后 $\alpha_{2}$ 的解是：

$\alpha_{2}^{new}$ = $\left\{\begin{matrix} H, \alpha _{2}^{new}>H\\ \alpha _{2}^{new} , L\leqslant \alpha _{2}^{new,unc} \leqslant H\\ L, \alpha _{2}^{new,unc} \leqslant L\\ \end{matrix}\right.$ ----------(10)

由 $\alpha_{2}^{new}$ 求得 $\alpha_{1}^{new}$ 是：

$\alpha_{1}^{new} = \alpha_{1}^{old} + y_{1}y_{2}(\alpha_{2}^{old} - \alpha_{2}^{new} )$ -----------(11)

要满足不等式约束，必须将其限制[L,H] 内，从而得到（10），由等式约束（5）得到（11），求解 $\alpha_{1}^{new}$ 。

上述过程可以简单叙述为，首先求解满足极值的α，然后求解满足在[0,C]区间的剪辑的α。

3.2 变量选择方法

第一个变量的选择方法： SMO称选择第一个变量为外层循环，外层循环在训练样本选择违反KKT条件最严重的样本点，并将其作为第一个变量。检验样本点是否满足KKT条件，即是否满足下列条件：

当 $\alpha _{i} = 0 \Rightarrow y_{i}g(x_{i}) \geqslant 1$

$0< \alpha _{i} < C \Rightarrow y_{i}g(x_{i}) = 1$

$\alpha _{i} = c \Rightarrow y_{i}g(x_{i}) \leqslant 1$

检验在 $\varepsilon$ 误差范围内进行，首先遍历整个样本集，选择违反KKT条件的 $\alpha _{i}$ 作为第一个变量，接着依据相关规则选择第二个变量，对这两个变量采用上述方法进行优化。当遍历完整个样本集后，遍历间隔边界上的（0< $\alpha _{i}$ <C）中违反KKT的 $\alpha _{i}$ 作为第一个变量，同样依据相关规则选择第二个变量，对此两个变量进行优化。当遍历完间隔边界样本集后，再次回到遍历整个样本集中寻找，即在整个样本集与间隔边界样本集上来回切换，寻找违反KKT条件的 $\alpha _{i}$ 作为第一个变量。直到遍历整个样本集后，没有违反KKT条件 $\alpha _{i}$ ，然后退出。

起初 $\alpha _{i}$ 都为0 ， $\alpha _{i}$ 很难变化，随着变量选择和二次优化的进行， $\alpha _{i}$ 符合 >0且<C 的数量越来越多， $\alpha _{i}$ 的变化幅度越来越大，两变量优化速度越来越快，直至没有变量违反KKT条件，即得到解。

第二个变量的选择： SMO称第二个变量的选择过程为内循环，假设在外循环中找个第一个变量记为 $\alpha _{1}$ ，第二个变量的选择希望能使 $\alpha _{2}$ 有较大的变换，由于 $\alpha _{2}$ 是依赖于| $E_{1}$ - $E_{2}$ |，当 $E_{1}$ 为正时，那么选择最小的 $E_{i}$ 作为 $E_{2}$ ，如果 $E_{1}$ 为负，选择最大 $E_{i}$ 作为 $E_{2}$ ，通常为每个样本的 $E_{i}$ 保存在一个列表中，选择最大的| $E_{1}$ - $E_{2}$ |来近似最大化步长。

特殊情况下，如果内层循环通过以上方法选择的 $\alpha _{i}$ 不能使目标函数有足够的下降，则采用以下启发式方法继续选择 $\alpha _{2}$ 。

首先在间隔边界集上选择能够使函数值足够下降的样本作为第二个变量，
如果间隔边界集上没有，则在整个样本集上选择第二个变量，
如果整个样本集依然不存在，则重新选择第一个变量。

3. 3 计算阈值b 和差值 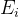$E_{i}$

每次完成两个变量的优化后，都要重新计算阈值b。当 $0 < \alpha _{1}^{new} < C$ 时，可以解出：

$b_{1}^{new} = - E_{1} - y_{1}K_{11}(\alpha _{1}^{new} - \alpha _{1}^{old} ) - y_{2}K_{21}(\alpha _{2}^{new} - \alpha _{2}^{old} ) + b^{old}$

$b_{2}^{new} = - E_{2} - y_{1}K_{12}(\alpha _{1}^{new} - \alpha _{1}^{old} ) - y_{2}K_{22}(\alpha _{2}^{new} - \alpha _{2}^{old} ) + b^{old}$

如果 $\alpha _{1}^{new}$ 、 $\alpha _{2}^{new}$ 同时满足 $0 < \alpha _{i}^{new} < C$ 则 $b _{1}^{new}$ = $b _{2}^{new}$ 如果 $\alpha _{1}^{new}$ 、 $\alpha _{2}^{new}$ 是 0 或C ，则 $b _{1}^{new}$ 和 $b _{2}^{new}$ 及他们之间的数都是符合KKT条件的阈值，这时一般选择他们的中点作为 $b _{}^{new}$ 。

在每次完成两个变量优化之后，还必须更新对应的 $E_{i}$ 值，并将他们保存在列表中，更新公式如下：

$E_{i}^{new}$ = $\sum_{S}^{}y_{j}\alpha _{j}K(x_{i},x_{j}) + b^{new} - y_{i}$

其中S 是所有支持向量 $x_{j}$ 的集合。

四、附注

本文主要摘自《统计学习方法》（李航，第二版）和引用网友相关资料，按照作者的理解梳理和整理而成，以供学习和参考使用。

reept

关注

8
点赞
踩
8

收藏

觉得还不错? 一键收藏
0
评论
支持向量机（Supporting Vector Machine）SMO（Sequential Minimal Optimization）算法

SMO算法的基本想法是：如果所有变量的解都满足此最优化问题的KKT条件，那么此时的所有变量就对应这个最优化问题的一个解。否则，选择这些变量中的两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。这样的凸二次规划问题，具有全局最优解，有许多优化算法可以用于这一问题的求解,但是当样本容量很大时，很多算法的时间复杂度和空间复杂度都会迅速增加，以致无法使用。当遍历完间隔边界样本集后，再次回到遍历整个样本集中寻找，即在整个样本集与间隔边界样本集上来回切换，寻找违反KKT条件的。
复制链接

扫一扫

专栏目录