老生常谈-01背包

        01背包这个问题，已经被表的不能再表了。然而为了加深理解，我还是要再把他拖出来表一次。

每个学DP的人，必然要接触到01背包。01背包这个问题的意义也像他的名字——从0到1，从不会到理解动态规划。这一步，天资聪颖的可能要几天，略微愚钝的可能就要十天半个月来理解，因此也可以说，01背包是新手进阶动态规划问题的第一个门槛。

         01背包问题，简而言之，就是给一个容量V有限的背包，和若干个有体积Vi和价值Wi的物品，要求从物品中选择若干个填充入背包，使背包物品的总价值最大。

        第一次接触到这种题目，很容易会想到使用贪心策略。对每个物品，按照价值/体积（性价比）进行排序，然后从高到底选择——然而这么做，非常容易陷入贪心算法的陷阱。很简单的数据，设背包容量为10，a，b，c三个物品的体积和价值分别是1 2,1 3,10,6；按照贪心算法，会选择a和b做最优解，很显然，最优解是只放c这个物品。

        那么可不可以用回溯来计算呢？答案是可以的。每次对当前物品进行分析，如果可行那么放入背包，并将该物品作为左节点，继续向下遍历。当遍历到不可行结果时，回溯再遍历右节点。当所有结点遍历完成，取值最大的解为最优解。然而这种算法效率堪忧，若物品的数量非常大，那回溯时需要的内存开销和时间开销也是惊人的。

        那么，假设你正在进行这个操作，你的面前有一个背包，若干物品，你会怎么放呢？

        不难想象，我们会拿起一件物品，放入背包，然后拿起第二件物品进行比对。直到我们将背包填到一个快要满的值的时候，我们拿起新的物品和背包中已有的物品作比较，然后选择放入或者丢弃——bingo！背包问题，特点就是每一件物品的状态，只有”放入“和”不放入“，而是否放入这件物品，只取决于”放入上一件物品后的状态“。

        现在把这段话抽象一下，用F[i][j]表示前i件物品中选取若干件物品放入剩余空间为j的背包中所能得到的最大价值。根据第i件物品放或不放进行决策

                                               

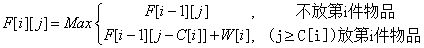
        其中F[i-1][j]表示前i-1件物品中选取若干件物品放入剩余空间为j的背包中所能得到的最大价值；

        而F[i-1][j-C[i]]+W[i]表示前i-1件物品中选取若干件物品放入剩余空间为j-C[i]的背包中所能取得的最大价值加上第i件物品的价值。

        根据第i件物品放或是不放确定遍历到第i件物品时的状态F[i][j]。

        设物品件数为N，背包容量为V，第i件物品体积为C[i]，第i件物品价值为W[i]。

用大白话讲，什么意思呢？就是，你这件物品放不放，取决于你上一件物品放不放，你上一件物品放不放，取决于你上上一件物品放不放……直到问题转移到第一件物品放不放，然后根据第一件的状态，可以求得最终的状态。

我们将状态，保存在一个大小为N*V的数组中。N是物品数，V是体积，该数组的意义如其名字——当放入N件物品时，容积剩余为V的背包能放物品的最大价值。这种算法，时间复杂度和空间复杂度都是O(NV)。时间复杂度上，经过严（bie）格（ren）的证明，已经被证明是基本不能再优化的。然而空间复杂度却可以继续优化。

如何优化？先写一写上面的代码吧。

for(int i = 1;i<n+1;i++)
{
	for(int j = 1;j<m+1;j++)
	{
		//当物品为i件重量为j时，如果第i件的重量(w[i-1])小于重量j时，c[i][j]为下列两种情况之一：
		//(1)物品i不放入背包中，所以c[i][j]为c[i-1][j]的值
		//(2)物品i放入背包中，则背包剩余重量为j-w[i-1],所以c[i][j]为c[i-1][j-w[i-1]]的值加上当前物品i的价值
		if(w[i-1]<=j)
		{
			if(c[i-1][j]<(c[i-1][j-w[i-1]]+p[i-1]))
			c[i][j] = c[i-1][j-w[i-1]]+p[i-1];
			else
			c[i][j] = c[i-1][j];
		}
		else
		c[i][j] = c[i-1][j];
	}
}

        可以看到，影响时间的是两层循环，1-N和1-V（M）的循环。而f[i][v]=max(f[i-1][v],f[i-1][v-c[i]]+w[i])这一句，就是我们需要的状态转移方程。画两个表吧。

表1-1背包问题数据表

物品号i	1	2	3	4	5	6
体积C	2	3	1	4	6	5
价值W	5	6	5	1	19	7

 

表1-2前i件物品选若干件放入空间为j的背包中得到的最大价值表

	0	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	5	5	5	5	5	5	5	5	5
2	0	5	6	6	11	11	11	11	11	11	11
3	0	5	5	10	11	11	16	16	16	16	16
4	0	5	5	10	11	11	16	16	16	16	17
5	0	5	5	10	11	11	19	24	24	29	30
6	0	5	5	10	11	11	19	24	24	29	30

        从表中可以看出，每一行，我们只需要一个状态，然后就跳跃进了下一列。另外n-1个状态都是没用的，并没有储存什么东西。也就是说，我们的状态数组其实可以压缩到f[v]这样的一个数组中。如何压缩呢？f[i][v]是由f[i-1][v]和f[i-1][v-c[i]]两个子问题递推而来，能否保证在推f[i][v]时（也即在第i次主循环中推f[v]时）能够得到f[i-1][v]和f[i-1][v-c[i]]的值呢？事实上，这要求在每次主循环中我们以v=V..0的顺序推f[v]，这样才能保证推f[v]时f[v-c[i]]保存的是状态f[i-1][v-c[i]]的值。再看一次状态转移方程吧，i-1有什么卵用么？似乎并没有。

于是我们得到了新的转移方程，f[v]=max{f[v],f[v-c[i]]}。代码如下：

for (i=1;i<=n;i++)
		for (j=t;j>=m[i];j--)
		{
			if (f[j]<f[j-m[i]]+w[i]) 
				f[j]=f[j-m[i]]+w[i];
		}	

        我对背包的理解也止步于此了。下面引用一段DD大神的话吧。

初始化的细节问题

        我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。有的题目要求“恰好装满背包”时的最优解，有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。

如果是第一种问法，要求恰好装满背包，那么在初始化时除了f[0]为0其它f[1..V]均设为-∞，这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。

        如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该将f[0..V]全部设为0。

为什么呢？可以这样理解：初始化的f数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量为0的背包可能被价值为0的nothing“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，它们的值就都应该是-∞了。如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。

        这个小技巧完全可以推广到其它类型的背包问题，后面也就不再对进行状态转移之前的初始化进行讲解。