限制玻尔兹曼机（Restricted Boltzmann Machine）学习笔记（一）

最新推荐文章于 2024-10-09 11:29:19 发布
最新推荐文章于 2024-10-09 11:29:19 发布
阅读量5.4w 收藏 48
点赞数 8
分类专栏： 算法与数学
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/roger__wong/article/details/43374343
版权


一、限制玻尔兹曼机的感性认识

要回答这个问题大概还要从神经网络说起。
（1）人工神经网络（artificial neural network）

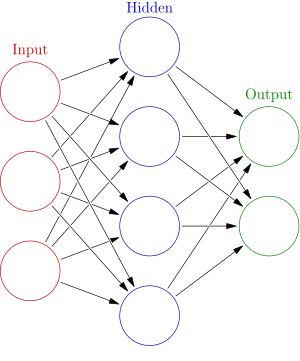
一言以蔽之，人工神经网络用于学习一个输入到输出的映射，通常由三层组成，输入层，隐层和输出层。
各层之间的每个连接都有一个权值，人工神经网络的训练过程就是学习这个权值。典型的，可以使用随机梯度下降法。
（2）递归人工神经网络（recurrent neural net
最低0.47元/天 解锁文章
受限玻尔兹曼机：原理、实现、与神经网络对比及应用
进一步有进一步的欢喜~
02-01 881
受限玻尔兹曼机（Restricted Boltzmann Machine, RBM）是一种强大的生成式随机神经网络，在机器学习和深度学习领域有着广泛的应用。本文将深入探讨受限玻尔兹曼机的原理，详细介绍其与玻尔兹曼分布的关系、“受限”的含义以及对比散度算法这一核心训练方法。同时给出使用 Python 和 NumPy 库实现受限玻尔兹曼机的具体代码。此外，还会将受限玻尔兹曼机与传统神经网络从原理、训练方式、损失函数、优缺点和适用场景等角度进行详细对比，最后通过手写数字识别的示例展示其应用。
【深度学习基础模型】玻尔兹曼机BM|受限玻尔兹曼机RBM|深度置信网络DBN详细理解并附实现代码。
985小水博的摸鱼日常
10-01 1235
玻尔兹曼机BM|受限玻尔兹曼机RBM|深度置信网络DBN，学习笔记！
Boltzmann Machine玻尔兹曼机
wulimmya的博客
07-16 4104
本文参考Hinton发表于2007年的一篇论文，链接在此 本渣英语并不是很烂，但最近发现看长篇的英文文献总是看的时候很明白，但眼睛拿开就特别容易忘记···所以很多重点我翻译过来，变成中文一下爽多了。并不是完全不看英文哈，毕竟地道和专业的文献写作技术还是需要不断打磨的，而且很多时候只看单一语言不容易懂，偶尔你只看中文会很迷惑，看看原英文就一下明白了，因为翻译毕竟不能传神，有时候只看英文也会很迷惑，...
Boltzmann machine
yiyiyi4321的专栏
05-27 821
翻译自网页：http://www.scholarpedia.org/article/Boltzmann_machine
Boltzmann 玻尔兹曼机（BM）
11-09 2536
Hopfield + 模拟退火 ⇒ Boltimann machine（随机神经网络）
28 玻尔兹曼机 Boltzmann Machine
cengjing12的博客
06-15 1650
玻尔兹曼机（Boltzmann Machine）在“受限玻尔兹曼机”那一章就有了简单的描述。在那一章我们就较为详细的分析过了，由于Boltzmann machine 中的依赖关系过于复杂，它的Learning 和Inference问题基本是intractable。所以，为了简化而提出了受限玻尔兹曼机（Restricted Boltzmann Machine）。 但是，为什么又重新谈谈这个似乎不太好的模型呢？主要原因是Boltzmann Machine 是深度信念网络（DBN），前馈神经网络等网络结构的基础，
受限玻尔兹曼机二
西檬饭
07-06 582
博主falao_beiliu写的一篇非常好的文章。 这里为方便自己以后速查，做个导航。 原文目录： 限制波尔兹曼机RBM使用方法 限制波尔兹曼机RBM能量模型 从能量模型到概率 求解极大似然 用到的抽样方法 马尔科夫蒙特卡罗简介 参考文献 原文链接： https://blog.csdn.net/mytestmy/article/det...
受限玻尔兹曼机(RBM)学习笔记
06-06
受限玻尔兹曼机（Restricted Boltzmann Machine, RBM）是一种无监督学习的神经网络模型，它在机器学习领域，特别是在深度学习中扮演着重要角色。RBM由加拿大计算机科学家Geoffrey Hinton等人提出，主要用于特征学习...
深度学习笔记：RBM限制玻尔兹曼机详解
"这篇内容是关于深度学习中的限制玻尔兹曼机(Restricted Boltzmann Machine, RBM)的读书笔记，主要介绍了RBM的基本结构、参数以及其功能。" 在深度学习领域，限制玻尔兹曼机(Restricted Boltzmann Machine, RBM)是...
机器学习笔记之受限玻尔兹曼机(二)模型表示
静静的学习就好
12-03 1088
上一节基于马尔可夫随机场介绍了玻尔兹曼分布，本节将介绍受限玻尔兹曼机的模型表示(Representation)与学习任务(Laerning)。
【机器学习手写笔记】Boltzmann Machine——玻尔兹曼机
yao09605的博客
04-25 566
受限玻尔兹曼机的英文详细介绍（论文）
04-08
详细介绍了受限玻尔兹曼机的原理，需要有一定的英文和数学功底。
受限制玻尔兹曼机
yanxiaopan的博客
03-03 424
http://blog.csdn.net/itplus/article/details/19168937
限制玻尔兹曼机 Restricted Boltzmann Machine (RBM)
Xyzx043874的博客
05-21 2613
1.基础知识要理解限制玻尔兹曼机，需要的基础知识为： 1.最大似然估计,这是我的上一篇博客。 2.玻尔兹曼分布(Boltzmann distribution) Boltzmann分布是一个系统中各种状态时，粒子的概率分布，概率测量或频率分布：F(state)∝e−EkTF(state)\propto e^-\frac{E}{kT} ∝\propto是正比于符号，EE是状态能量，kk是玻尔兹曼
Boltzmann机详解
qq_40641338的博客
04-08 5178
基于热力学的随机型神经网络–Boltzmann机 1. 模拟退火算法 我们知道，Hopfield神经网络拥有联想记忆的能力，这也是对生物神经网络的一种模拟。但是，Hopfield神经网络也和BP神经网络一样，有一个致命的缺陷：只能找到局部最优解，而无法沿着梯度上升的方向在全局的角度寻求全局最优解。 为了解决这个问题，1983年，Kirkpatrick等提出了模拟退火算法（SA）能有效的解决局部最优...
Boltzmann机
AIamateur的专栏
04-29 1270
http://www6.zzu.edu.cn/shili/jxzy/ICtrl/text/chapter6/section3/6.3.3.htmBoltzmann机网络结构和工作方式       Boltzmann机网络是一个相互连接的神经网络模型，具有对称的连接权系数，及 ，且。网络由可见单元（Visible Unit）和隐单元（Hidden Unit）构成。可见单元由输入、输出部分组成。每
限制波尔兹曼机 Restricted Boltzmann Machine | RBM
JasonH2021的博客
06-03 2078
本文主要简单介绍了限制玻尔兹曼机的基本概念，优缺点，应用场景，建模时的注意事项，评价指标，实现方法和python示例等。
玻尔兹曼机 BoltzmannMachine
最新发布
weixin_64404339的博客
10-09 1710
玻尔兹曼机，神经网络入门，概率能量模型
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值