update:
阅读过2000啦!
给大家弄个什么福利呢!
在评论告诉我吧!
update一个原文档的链接方便大家看看
快速傅里叶变换.docx
Fast Fourier Transformation
——By Rose_max
简单来说,傅里叶变换,在oi里面就一个用途:加速多项式乘法
方法就一个:构造多项式fft点值乘法ifft
写在前面
关于学习FFT算法的资料个人最推荐的还是算法导论上的第30章(第三版), 多项式与快速傅里叶变换, 基础知识都讲得很全面
FFT算法基本概念
FFT(Fast Fourier Transform) 即快速傅里叶变换, 是离散傅里叶变换的加速算法, 可以在O(nlogn)的时间里完成DFT, 利用相似性也可以在同样复杂度的时间里完成逆DFT
DFT(Discrete Fourier Transform) 即离散傅里叶变换, 这里主要就是多项式的系数向量转换成点值表示的过程
FFT算法需要的基础数学知识
1:多项式表达法
次数表达法:
次数界n(最高次数为n-1)的多项式: 的系数表达为一个由系数组成的向量a=(a0,a1,a2,…an-1)
点值表达法:
把多项式理解成一个函数,然后用函数上的点表示这个函数
(两点确定一条直线,三点确定一个二次函数…n+1个点确定一个n次函数,以此类推)
次数界为n的多项式的点值表达法就是一个n个点对组成的集合
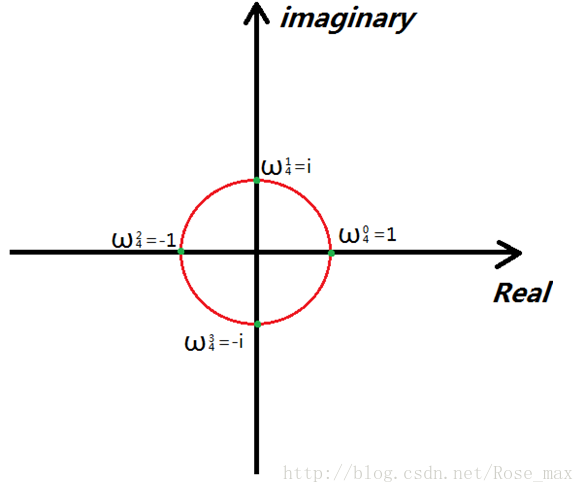
2:单位复数根
如果一个数的n次方能够变回1,那么我们叫他n次复数根,记作w_n^k
n次单位复数根刚好有n个, 他们是e^(2kπ/n i), k=0,1,2…n−1, 关于复数指数的定义如下:
e^ui=cos〖(u)+sin(u)〗 i
他们均匀的分布在了这个圆上,离原点的距离都是1
下图以四次单位复数根为例
消去引理: 对于任何整数n>=0,k>=0,以及d>0,有
w_dndk=w_nk
证明:
w_dndk=(e(2kπ/dn) )dk=(e(2kπ/n) )k=w_nk
推论:
w_n^(n/2)=w_2=-1
折半引理:如果n>0且n为偶数,那么n个n次单位复数根的平方的集合等于n/2个n/2次单位复数根的集合
证明:根据消去引理,我们有(w_n^k )2=w_(n/2)k。如果对所有n次单位复数根进行平方,那么我们刚好得到每个n/2次单位根两次。因为:
(w_n^(k+n/2) )2=w_n(2k+n)=w_n^2k w_nn=w_n2k=(w_n^k )^2
因此,w_nk与w_n(k+n/2)的平方相同
求和引理:对于任意整数n>=1和不能被n整除的非负整数k,有
∑_(j=0)(n-1)▒(w_nk )^j =0
证明:(等比数列)
∑_(j=0)(n-1)▒(w_nk )^j = ((w_n^k )n-1)/(w_nk-1)=((w_n^n )k-1)/(w_nk-1)=((1)k-1)/(w_nk-1)=0
DFT 离散傅里叶变换
我们希望次数界为n的多项式
A(x)=∑_(j=0)^(n-1)▒〖a_j x^i 〗
求出在w_n^0, w_n^1, w_n2…w_n(n-1)(即n个n次单位复数根)的值
使用插值法求,时间复杂度O(n^2)。这即是DFT(离散傅里叶变换)
FFT 快速傅里叶变换(分治!!!)
利用单位复数根的特殊性质(上面介绍的消去,折半,求和引理),我们可以在O(n〖 log〗n)的时间内计算出A(x)进行傅里叶变换后的点集
我们采用分治的策略,先分离出A(x)中的以奇数下标和偶数下标为系数的数,形成两个新的次数界为n/2的多项式A0(x)和A1(x)
A^0(x)=a_0+a_2 x+a_4 x^2+…+a_n x^(n/2-1)
A^1(x)=a_1+a_3 x+a_5 x^2+…+a_(n-1) x^(n/2-1)
那么我们可以很容易得到
A(x)= A0(x2)+xA1(x2) 为什么要乘一个x?因为我们要把奇数和偶数下标的数分开!!!!
所以,求A(x)在w_n^0, w_n^1, w_n2…w_n(n-1)处的值就转换成为
求A0(x)和A1(x)在(w_n^0 )^2, (w_n^1 )2,(w_n2 )2…(w_n(n-1) )^2处的值
根据折半引理,上式并不是由n个不同值组成,而是仅仅由n/2个n/2次单位复数根组成,每个根正好出现两次。
所以,我们就可以递归求值啦,每次规模变为原来的一半
那么,我们就可以把一个n个元素的DFT的计算,换为两个规模为n/2个元素的DFT计算
边界问题:由于w_10=1,所以w_10a=a啦
如下,举个现实点的栗子
然后把当前的单位复数根平方进FFT,计算G(x)与H(x)
当然啦,代入的单位复数根一定要是不一样的。这里我们的递归求复数根会帮我们解决这个问题
IFFT 快速傅里叶逆变换
具体思路就是在单位复数根处插值
证明详见《算法导论(第三版)》P535页或本文件夹IFFT证明
结论:我们用w_n^(-1)代替w_n,并将结果每个除以n。得到的便是逆DFT的结果
代码实现
首先确定一点:我们的a数组是什么?
a[i]表示 代入n次单位负数根第i个(比作x) 得到的值(比作y)
(FFT的递归实现)
在第2~3行,n等于1的时候,w_1^0=1,那么他的DFT值就是自己a
第4行,定义了w_n作为n次单位复数根。由于我们知道
e^ui=cos〖(u)+sin(u)〗 i 和 e^(2kπ/n i)
那么我们可以轻易得到主单位复数根(次方也就是k为1)的值为
cos(2π/n)+sin(2π/n*op)
至于op是什么??这是为了做FFT的逆运算所增加的变量
我们根据IFFT中得出的结论,使用w_n^(-1)代替w_n并在最后除以n即为结果
第6~7行,对a数组进行奇偶分离
第8~9行,对于k=0,1,2,n/2-1
我们有
11~12行,我们通过递归变换的结果,得到我们y数组的值
对于k=0,1,2,…,n/2-1,我们能得出y0,y1,y2,…,yn/2-1
同理,也可以得出y_(n/2), y_(n/2+1),…, y_(n-1)
这里的w_n2k实质上是w_(n/2)k表示是n/2次单位复数根
所以,FFT返回的确实是A数组的FFT值
Tips:FFT的递归代码短且容易理解。但是本代码使用了C++库中自带的Complex函数,所以效率较慢。并且由于递归的原因,单位复数根容易损失精度且处理范围不能太大,约为〖10〗^4左右。具体优化接下来再讲。代码详见文件夹内FFT递归模版
——大佬请54此条
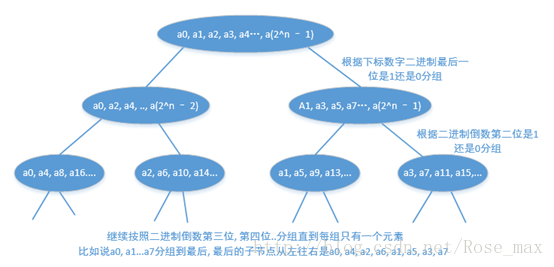
快速傅里叶变换迭代法
上面说过,递归实现FFT的做法容易爆栈。而且时间较长。
那么我们可以实现一种迭代法
通过上图我们可以看出,最后一层的子节点下标其实是
其下标转化为二进制串的倒序字符串按照字典序排列的顺序!
举个栗子:
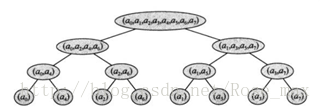
递归n=8后产生的向量树
可以看到下标依次为
a_0,a_4,a_2,a_6,a_1,a_5, a_3,a_7
二进制码为
000,100,010,110,001,101, 011,111
反转后
000,001,010,011,100,101,110,111
很容易可以看出他们是递增的对吧
所以我们可以得出以上结论!
那么我们可以在O(nlogn)的时间内得到最下面一层的顺序。
有两种方法:雷德算法 or 类似数位DP的做法
依次做FFT操作并向上倍增合并结果,可以避免使用递归
时间复杂度:
几个小优化
1:在计算递归回来的孩子上传值给父亲中,我们发现w_n^k a_k^1被重复计算了。可以使用一个y存储计算结果,并直接最后减去或者增加即可(蝴蝶操作)
2:我们在计算单位复数根时,有两种方法
通过递归计算或者通过数学方法(即指数定义)
通过递归计算,代码长度短且容易理解,但是在递归的过程中容易损失精度。约在10^14次方左右就会炸。
指数定义,代码较长,时间较短。本文暂时未给出
可以通过e^ui=cos〖(u)+sin(u)〗 i一式得出结果
3:推荐预处理单位复数根
如上所述,递归容易损失精度。我们可以使用一个数组存入单位复数根
后记:
总结一下FFT的优化思想
优化理念
一个小问题
可以很容易得知,FFT也可以用来计算大整数乘法
How?我们可以把一个大整数理解成
a[0]+a[1]*10+a[2]102+…+a[n]*10n
然后把10看成未知数,FFT求解即可
但是注意了,FFT取出的点,一定要足够生成新的多项式!!!!!
所以说L要取到n2次幂
FFT适用范围
只有在题目内构造出的多项式>=10^4次方时,FFT才可以派上用场,否则暴力可以解决。
因为FFT的代价是超级超级超级超级巨大的常数!!!!
慎 用
慎 用
慎 用
模版-caioj1450
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
struct Complex
{
double r,i;//real imag
Complex() {}
Complex(double _r,double _i){r=_r;i=_i;}
friend Complex operator + (const Complex &x,const Complex &y){return Complex(x.r+y.r,x.i+y.i);}
friend Complex operator - (const Complex &x,const Complex &y){return Complex(x.r-y.r,x.i-y.i);}
friend Complex operator * (const Complex &x,const Complex &y){return Complex(x.r*y.r-x.i*y.i,x.r*y.i+x.i*y.r);}
};
const double PI=acos(-1.0);
const int MAXN=1100010;
int R[MAXN],sum[MAXN];
char s1[MAXN],s2[MAXN];
Complex a[MAXN],b[MAXN];
void fft(Complex *y,int len,int on)
{
for(int i=0;i<len;i++)if(i<R[i]){Complex tt;tt=y[i];y[i]=y[R[i]];y[R[i]]=tt;}
for(int i=1;i<len;i<<=1)//枚举需要合并的长度 合并后的长度就成了i*2对吧。所以无需枚举至len
{
Complex wn(cos(PI/i),sin(on*PI/i));//无需乘2,因为合并后长度i*2,用到的单位复数根只有i
for(int j=0;j<len;j+=(i<<1))//被分成了L/(i<<1)段序列
{
Complex w(1,0);//注意一点,w是在for循环执行完毕后才累乘,因为我们还有w^0对吧
for(int k=0;k<i;k++,w=w*wn)//枚举前半部分,后半部分加上一个i就可以了嘛
{
Complex u=y[j+k];//j+k即是前半部分
Complex v=w*y[j+k+i];//j+k+i即是后半部分
y[j+k]=u+v;
y[j+k+i]=u-v;
}
}
}
if(on==-1)for(int i=0;i<len;i++)y[i].r/=len;//IFFT 每个数都要/len
}
int main()
{
scanf("%s",s1);
scanf("%s",s2);
int len1=strlen(s1),len2=strlen(s2);
int len=1,lenx=len1+len2;int L=0;
for(len=1;len<lenx;len<<=1)L++;
for(int i=0;i<len;i++)R[i]=((R[i>>1])>>1)|((i&1)<<(L-1));
for(int i=0;i<len1;i++)a[i]=Complex(s1[len1-i-1]-'0',0);
for(int i=len1;i<len;i++)a[i]=Complex(0,0);
for(int i=0;i<len2;i++)b[i]=Complex(s2[len2-i-1]-'0',0);
for(int i=len2;i<len;i++)b[i]=Complex(0,0);
fft(a,len,1);fft(b,len,1);
for(int i=0;i<len;i++)a[i]=a[i]*b[i];
fft(a,len,-1);
for(int i=0;i<len;i++)sum[i]=int(a[i].r+0.5);
for(int i=0;i<len;i++)
{
sum[i+1]+=sum[i]/10;
sum[i]%=10;
}
len=len1+len2-1;
while(sum[len]<=0 && len>0)len--;
for(int i=len;i>=0;i--)printf("%c",sum[i]+'0');
printf("\n");
return 0;
}













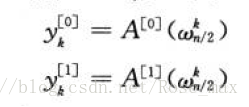
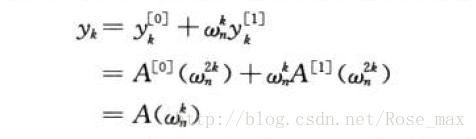
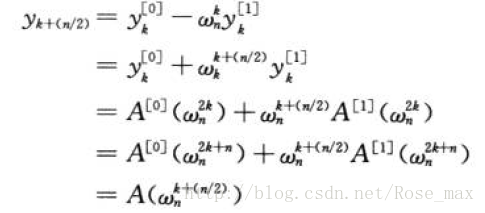














 3432
3432

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








