字符串匹配算法——KMP算法简单解释

一、字符串匹配算法KMP

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称KMP算法）。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。

二、KMP算法图解

这种算法在网上看了很多解释，大部分都比较晦涩复杂，直到看到了一篇文章才是真的简单易懂，包教包会，这里就按照自己的理解写一篇文章。
我们用一个例子来看，在字符串“WWE QWERQW QWERQWERQWRT”中查找是否含有另一个字符串“QWERQWR”。通常做法是将两个字符串进行一个个比对，当发现一个字符一致时，进行第二个字符的比对，如果发现不一致，再退回去从首字符的下一个开始进行新一轮比对，空口说不太好理解，下面我们结合图来看KMP算法是如何利用普通匹配失败的信息加快效率的。
1.

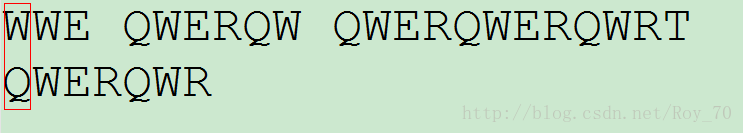
我们先将两个字符串的第一个字符进行比对，因为W和Q不匹配，因此跳到下个字符开始匹配。
2.

第二位的字符也不匹配，继续后移
3.

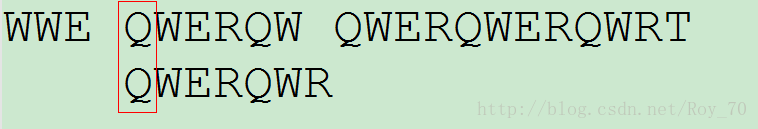
依次比对，直到发现第一个字符相同的情况
4.

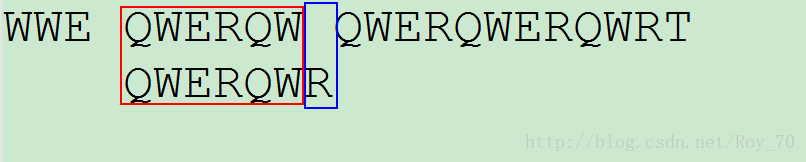
然后接着从第二个字符开始对应比对，直到有一个字符与搜索词对应不相同为止
5.
这时，朴素的对比方法是将搜索词后移一位，再从头逐个比对，例如：

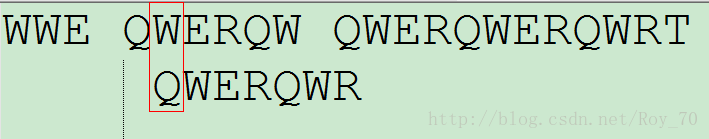
这种方法当然是可行的，但是就体现不出算法的高效了。
6.
而在KMP算法中，当我们知道空格和”R”不匹配时，我就相当于知道了它的前面六个字符是”QWERQW”，KMP算法中需要设法利用这个已知了的信息，让搜索位置后移提供效率。这里我们用到了一张表，叫做“部分匹配表”，后面我们会再说如何计算出这张表，这里我们只说如何使用。

搜索词	Q	W	E	R	Q	W	R
部分匹配值	0	0	0	0	1	2	0

7.

当我们知道空格和“R”不匹配时，前面六个字符是匹配的。查表可知，最后一个匹配字符W对应的部分匹配值是2，按照公式：
移动位数 = 已匹配的字符数 - 对应的部分匹配值
得到6 - 2 = 4，因此将搜索词向后移动4位。
8.

移动四位后比对，发现第三位不匹配，此时依据公式移动位数 = 已匹配字符数（2） - 对应的部分匹配值（0） = 2，因此继续向后移动两位
9.

第一位不匹配，向后移动一位

此时又是和第步骤7一样，继续移动6 - 2 = 4位
10.

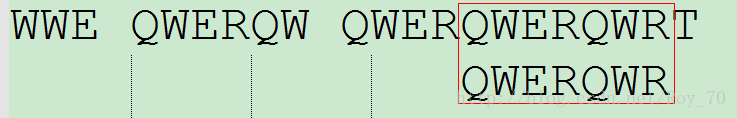
此时发现全部七位匹配相同，所以第一个搜索完成了，如果还需要继续搜索（查找所有匹配字段），就继续向后移动 = 7 - 0 位，下面就不在赘述了。

三、部分匹配表

接下来说一下部分匹配表是如何生成的。首先，要了解两个概念：”前缀”和”后缀”。 “前缀”指除了最后一个字符以外，一个字符串的全部头部组合；”后缀”指除了第一个字符以外，一个字符串的全部尾部组合。
例如：单词level的前缀有{l,le,lev,leve}四个，后缀有{evel,vel,el,l}四个，然后前缀和后缀集合取交集，得到{l}，只有一个元素，长度为1，因此level的部分匹配值就是1。

搜索词	Q	W	E	R	Q	W	R
部分匹配值	0	0	0	0	1	2	0

再回来看上面的字符串例子：
“Q”的前缀和后缀都为空集，共有元素的长度为0；
“QW”的前缀为[Q]，后缀为[W]，共有元素的长度为0；
“QWE”的前缀为[Q, QW]，后缀为[WE, E]，共有元素的长度0；
“QWER”的前缀为[Q, QW, QWE]，后缀为[WER, ER, R]，共有元素的长度为0；
“QWERQ”的前缀为[Q, QW, QWE, QWER]，后缀为[WERQ, ERQ, RQ, Q]，共有元素为”Q”，长度为1；
“QWERQW”的前缀为[Q, QW, QWE, QWER, QWERQ]，后缀为[WERQW, ERQW, RQW, QW, W]，共有元素为”QW”，长度为2；
“QWERQWR”的前缀为[Q, QW, QWE, QWER, QWERQ, QWERQW]，后缀为[WERQWR, ERQWR, RQWR, QWR, WR, R]，共有元素的长度为0。

“部分匹配”的实质是，有时候，字符串头部和尾部会有重复。比如，”QWERQW”之中有两个”QW”，那么它的”部分匹配值”就是2（”QW”的长度）。搜索词移动的时候，第一个”QW”向后移动4位（字符串长度-部分匹配值），就可以来到第二个”QW”的位置。

总之，KMP算法还是很巧妙的利用了已经得到的信息，这也正是算法巧妙的地方，积少成多，在大量的字符创匹配中带来的效率提升是好几倍的。KMP算法的代码实现在下一篇中给出，谢谢