旋转卡壳——凸多边形直径

出处：http://blog.csdn.net/acmaker/article/details/3177045

凸多边形直径

我们将一个多边形上任意两点间的距离的最大值定义为多边形的直径。 确定这个直径的点对数可能多于一对。 事实上， 对于拥有  n  个顶点的多边形， 就可能有  n  对“直径点对”存在。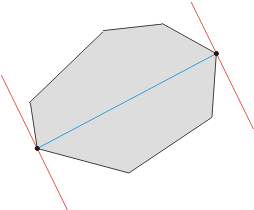 

 

一个多边形直径的简单例子如左图所示。 直径点对在图中显示为被平行线穿过的黑点 （红色的一对平行线）. 直径用浅蓝色高亮显示。

显然， 确定一个凸多边形  P  直径的点对不可能在多边形  P  内部。 故搜索应该在边界上进行。 事实上， 由于直径是由多边形的平行切线的最远距离决定的， 所以我们只需要查询 对踵点 。 Shamos (1978) 提供了一个 O(n)  时间复杂度计算n点凸包对踵点对的算法。直径通过遍历顶点列表， 得到最大距离即可。 如下是1985年发表于 Preparata 和 Shamos 文章中的 Shamos 算法的伪代码。 
输入是一个多边形  P ={ p1 ,..., pn }. 

begin
     p0:=pn;
     q:=NEXT[p];
     while (Area(p,NEXT[p],NEXT[q]) > Area(p,NEXT[p],q)) do
          q:=NEXT[q];
          q0:=q;
          while (q != p0) do
               begin
                    p:=NEXT[p];
                    Print(p,q);
                    while (Area(p,NEXT[p],NEXT[q]) > Area(p,NEXT[p],q) do
                         begin
                              q:=NEXT[q];
                              if ((p,q) != (q0,p0)) then Print(p,q)
                              else return
                         end;
                    if (Area(p,NEXT[p],NEXT[q]) = Area(p,NEXT[p],q)) then
                      if ((p,q) != (q0,p0)) then Print(p,NEXT[q])
                      else Print(NEXT[p],q)
               end
end.

此处  Print(p,q)  表示将  (p,q)  作为一个对踵点对输出，  Area(p,q,r)  表示三角形  pqr  的有向面积。 
虽然直观上看这个过程与常规旋转卡壳算法不同， 但他们在本质上是相同的， 并且避免了所有角度的计算。 

如下是一个更直观的算法：

1. 计算多边形 y 方向上的端点。 我们称之为 ymin 和 ymax 。
2. 通过 ymin 和 ymax 构造两条水平切线。 由于他们已经是一对对踵点， 计算他们之间的距离并维护为一个当前最大值。
3. 同时旋转两条线直到其中一条与多边形的一条边重合。
4. 一个新的对踵点对此时产生。 计算新的距离， 并和当前最大值比较， 大于当前最大值则更新。
5. 重复步骤3和步骤4的过程直到再次产生对踵点对 (ymin,ymax) 。
6. 输出确定最大直径的对踵点对。

至此， 上述的过程（伪代码中的）显得十分有用， 我们可以从对踵点对中得到其他的信息， 如多边形的 宽度 。