自协方差函数，自相关函数，协方差矩阵

1．自相关函数(Autocorrelation function)

自相关函数是描述随机信号X(t)在任意两个不同时刻t₁，t₂，的取值之间的相关程度

2. 自协方差函数(Autocovariance function)

自协方差函数是描述随机信号X(t)在任意两个不同时刻t₁，t₂，的取值之间的二阶混合中心矩，用来描述X(t)在两个时刻取值的起伏变化（相对与均值）的相关程度，也称为中心化的自相关函数。

当时， 

显然，自协方差函数和自相关函数描述的特性基本相同。

3. 协方差矩阵

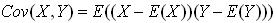
记住，X、Y是一个列向量，它表示了每种情况下每个样本可能出现的数。比如给定

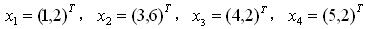
由于数据是二维的，所以协方差矩阵是一个2*2的矩阵，矩阵的每个元素为：元素(i,j) = (第 i 维所有元素 - 第 i 维的均值) * (第 j 维所有元素 - 第 j 维的均值) 。

其中「*」代表向量内积符号，即两个向量求内积，对应元素相乘之后再累加。

我们首先列出第一维：D1: (1,3,4,5) 均值：3.25

D2: (2,6,2,2) 均值：3

下面计算协方差矩阵第(1,2)个元素：

元素(1,2)=(1-3.25,3-3.25,4-3.25,5-3.25)*(2-3,6-3,2-3,2-3)=-1

类似的，我们可以把2*2个元素都计算出来：

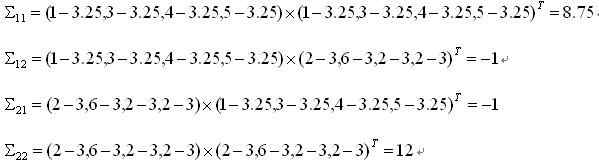
这个题目的最终结果就是：

用matlab计算这个例子

z=[1,2;3,6;4,2;5,2]

cov(z)

ans =

    2.9167   -0.3333

   -0.3333    4.0000

可以看出，matlab计算协方差过程中还将元素统一缩小了3倍。所以，协方差的matlab计算公式为：

    协方差(i,j)=（第i列所有元素-第i列均值）*（第j列所有元素-第j列均值）/（样本数-1）

参考：

[1] http://en.wikipedia.org/wiki/Covariance_matrix

[2] http://www.cnblogs.com/cvlabs/archive/2010/05/08/1730319.html

[3]http://blog.csdn.net/ybdesire/article/details/6270328

[4] http://202.117.122.42:9001/xhxt/xhyxt/xuexi/chart9/c_9_2_3_001.htm