算法练习：两指针之三数之和为0

问题描述

给出一个整型数组，找出所有三个元素的组合，其组合之和等于0。要求在结果集里不含有重复的组合。

举例：

输入{-2， 1， -1， 2， 1}

输出{-2， 1， 1 }

 

问题分析

最容易想到的是穷举法，挑选第一个元素，然后在其后挑选第二个元素，再从除已经挑选出的两个元素之外挑第三个元素，判断三者之和是否为0；第二种想到的是用回溯递归，这两种方法的时间复杂度均为O(n^3)，可参阅代码部分关于这两种方法的实现。

那有没有复杂度低一些的呢，答案是有的，就是使用两指针的方法，从而使复杂度下降到O(n^2)。

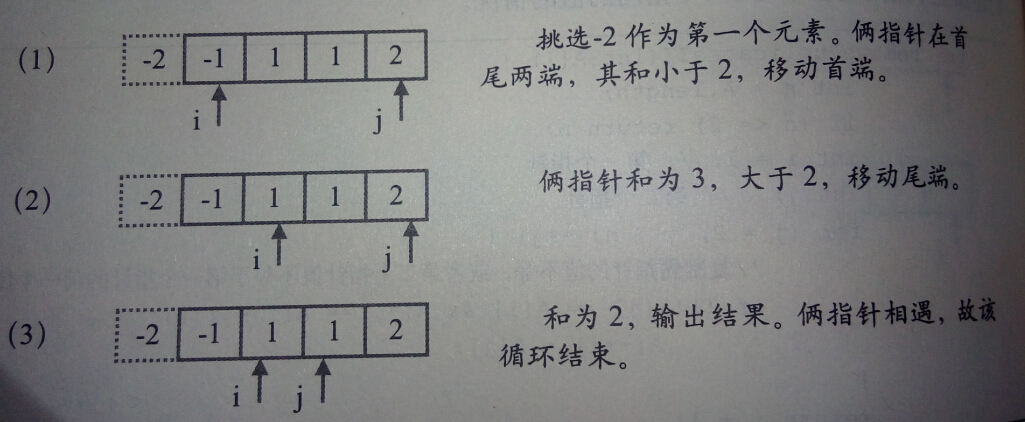
首先，将数组按从小到大的排序，然后从头挑选一个元素，接着使用首尾两个指针来挑选后两个元素。如图所示（可结合后面实现代码理解）：

 

 

代码实现

 

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;


typedef vector<int> IntArray;
typedef vector<IntArray> ResultSet;


ResultSet gResultSet;	//结果集


//穷举法
void GetResultSet( const IntArray& mSrcArray )
{
	for( int i = 0; i < mSrcArray.size();  )
	{
		for( int j = i + 1; j < mSrcArray.size();  )
		{
			for( int k = j + 1; k < mSrcArray.size();  )
			{
				if ( ( mSrcArray[i] + mSrcArray[j] + mSrcArray[k] ) == 0 )
				{
					IntArray mTempArray;
					mTempArray.push_back( mSrcArray[i] );
					mTempArray.push_back( mSrcArray[j] );
					mTempArray.push_back( mSrcArray[k] );
					gResultSet.push_back( mTempArray );
				}

				//避免重复
				do{ ++k; } while( k < mSrcArray.size() && mSrcArray[k-1] == mSrcArray[k] );
			}
			//避免重复
			do{ ++j; } while( j < mSrcArray.size() && mSrcArray[j-1] == mSrcArray[j] );
		}
		//避免重复
		do{ ++i; } while( i < mSrcArray.size() && mSrcArray[i-1] == mSrcArray[i] );
	}
}


//两指针法
void GetResultSet_2Ptr( const IntArray& mSrcArray ) 
{
	for( int k = 0; k < mSrcArray.size(); ++k )
	{
		//第一个数大于0，因为是从小到大排了序的，所以以下就不可能了。
		if ( mSrcArray[k] > 0 ) break;

		//去除重复结果
		if ( k > 0 && mSrcArray[k] == mSrcArray[k-1] ) continue;

		int i = k + 1;
		int j = mSrcArray.size()-1;

		//两指针向中间靠拢找结果
		while( i < j )
		{
			int sum = mSrcArray[i] + mSrcArray[j] + mSrcArray[k];

			//和过小，左边指针移动
			if ( sum < 0 )
			{
				++i;
			}
			//和过大，右边指针移动
			else if ( sum > 0 )
			{
				--j;
			}
			//找到一个结果
			else
			{
				IntArray mTempArray;
				mTempArray.push_back( mSrcArray[k] );
				mTempArray.push_back( mSrcArray[i] );
				mTempArray.push_back( mSrcArray[j] );
				gResultSet.push_back( mTempArray );

				//避免重复
				do{ ++i; } while( i < j && mSrcArray[i-1] == mSrcArray[i] );

				//避免重复
				do{ --j; } while( i < j  && mSrcArray[j] == mSrcArray[j+1] );
			}
		}


	}
}


//回溯法(递归)
void GetResultSet_Recursive( const IntArray& mSrcArray, IntArray& mDstArrayTemp, int iStart, int nTarget )
{
	if ( nTarget == 0 && mDstArrayTemp.size() == 3 )
	{
		gResultSet.push_back( mDstArrayTemp );
	}
	else
	{
		for( int i = iStart; i < mSrcArray.size(); ++i )
		{
			//数量已经超过3，不能再加入了
			if ( mDstArrayTemp.size() >= 3 ) break;

			//避免重复加入
			if ( i > iStart && mSrcArray[i] == mSrcArray[i-1] ) continue;

			mDstArrayTemp.push_back( mSrcArray[i] );

			GetResultSet_Recursive( mSrcArray, mDstArrayTemp, i+1, nTarget + mSrcArray[i] );

			//回溯
			mDstArrayTemp.pop_back();
		}
	}
}



//打印结果集  
void OutSubSets()  
{  
	for( ResultSet::iterator it = gResultSet.begin();  
		it != gResultSet.end(); ++it )  
	{   
		for( IntArray::iterator itTemp = it->begin();   
			itTemp != it->end(); ++itTemp )  
		{  
			cout << *itTemp << " ";  
		}  
		cout << endl;  
	}  
	cout << "--------------------------------------------" << endl;  
}  


int main()
{
	IntArray mSrcArray;  
	int nTemp;  
	while( true )  
	{  
		mSrcArray.clear();  
		while( cin >> nTemp )  
		{  
			if ( nTemp == 0 ) break;  
			mSrcArray.push_back( nTemp );  
		}  

		//排序  
		sort( mSrcArray.begin(), mSrcArray.end() );  


		gResultSet.clear();  
		//GetResultSet( mSrcArray ); 
		//GetResultSet_2Ptr( mSrcArray );

		IntArray mDstArrayTemp;
		GetResultSet_Recursive( mSrcArray, mDstArrayTemp, 0, 0 );

		

		//打印结果集  
		OutSubSets();  
	}  


	return 0;
}

系列文章说明:
1.本系列文章[算法练习],仅仅是本人学习过程的一个记录以及自我激励,没有什么说教的意思。如果能给读者带来些许知识及感悟，那是我的荣幸。
2.本系列文章是本人学习陈东锋老师《进军硅谷，程序员面试揭秘》一书而写的一些心得体会，文章大多数观点均来自此书，特此说明！
3.文章之中,难免有诸多的错误与不足,欢迎读者批评指正,谢谢.

作者：山丘儿
转载请标明出处，谢谢。原文地址：http://blog.csdn.net/s634772208/article/details/46729197