hdu 4780 Candy Factory(最小费用流）

Candy Factory

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 541    Accepted Submission(s): 265

Problem Description

  A new candy factory opens in pku-town. The factory import M machines to produce high quality candies. These machines are numbered from 1 to M.
  There are N candies need to be produced. These candies are also numbered from 1 to N. For each candy i , it can be produced in any machine j. It also has a producing time(s _i,t _i) , meaning that candy i must start producing at time s _i and will finish at t _i. Otherwise if the start time is p _i(s _i < p _i < t _i) then candy will still finish at t _i but need additional K*(p _i - s _i) cost. The candy can’t be produced if p _i is greater than or equal to t _i. Of course one machine can only produce at most one candy at a time and can’t stop once start producing.
  On the other hand, at time 0 all the machines are in their initial state and need to be “set up” or changed before starting producing. To set up Machine j from its initial state to the state which is suitable for producing candiy i, the time required is C _ij and cost is D _ij. To change a machine from the state suitable for candy i ₁ into the state suitable for candy i ₂, time required is E _i1i2 and cost is F _i1i2.
  As the manager of the factory you have to make a plan to produce all the N candies. While the sum of producing cost should be minimized.

 

Input

　　There are multiple test cases.
　　For each case, the first line contains three integers N(1<=N<=100), M(1<=M<=100), K(1<=K<=100) . The meaning is described above.
　　Then N lines follow, each line contains 2 integers s _i and t _i(0 <= s _i < t _i <100000).
　　Then N lines follow, each line contains M integers, the j-th integer of the i-th line indicating C _ij(1<=C _ij<=100000) .
　　Then N lines follow, each line contains M integers, the j-th integer of the i-th line indicating D _ij(1<=D _ij<=100000) .
　　Then N lines follow, each line contains N integers, the i ₂-th integer of the i ₁-th line indicating E _i1i2(1<=E _i1j2<=100000) .
　　Then N lines follow, each line contains N integers, the i ₂-th integer of the i ₁-th line indicating F _i1i2(1 <= F _i1j2<=100000) .
　　Since the same candy will only be produced once, E _ii and F _ii are meaningless and will always be -1.
　　The input ends by N=0 M=0 K=0. Cases are separated with a blank line.

 

Output

  For each test case, if all of M candies can be produced, output the sum of minimum producing cost in a single line. Otherwise output -1.

 

Sample Input

  
  

   
   3 2 1
4 7
2 4
8 9
4 4
3 3
3 3
2 8
12 3
14 6
-1 1 1
1 -1 1
1 1 -1
-1 5 5
5 -1 5
5 5 -1

1 1 2
1 5
5
5
-1
-1

0 0 0
  
  

 

Sample Output

  
  

   
   11
-1


   
   

    
    

     
     Hint
    
    
For the first example, the answer can be achieved in the following way:

    
    
     
     
    
     
	In the picture, S i represents setting up time for candy i, A i  represents changing time  for candy i  and P i represents producing time for candy i .
	So the total cost includes: 
　　setting up machine 1 for candy 1, costs 2
　　setting up machine 2 for candy 2, costs 3
　　changing state from candy 2 to candy 3, costs 5
　　late start of candy 2, costs 1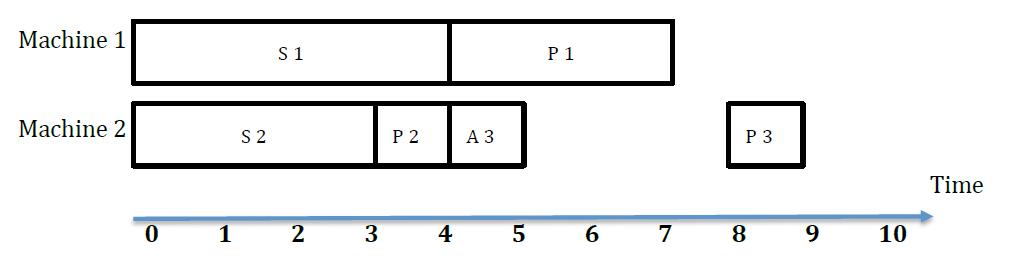 

   
   
   
    
  
  

 

Source

2013 Asia Hangzhou Regional Contest

 



题目链接： http://acm.hdu.edu.cn/showproblem.php?pid=4780

题目大意：略，太长了，不好解释。

题目思路：最小费用流，主要体现在如何建图。拆点必须要有，每个糖果只能制造一次，糖果分为左右点。
建图：
    1.源点接机器。花费0，流量1（每台机器只能初始化一次）；
    2.糖果之间的连接。若糖果i做完，还能做糖果j,则连接（i的左点连j右点）。花费为机器转化+可能的超时费用。流量为1（一个糖果只能一台机器做）；
    3.机器和糖果的连接。连糖果的右点。花费为机器初始化+可能的超时费用，流量为1（初始化一次）；
    4.糖果和汇点的连接。花费0，流量1.
    5.源点和糖果的连接。 连接糖果的左点。这里计算的都是已经初始化过的机器来做糖果，根据糖糖的连接应该不难理解。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<vector>
#include<queue>
#define inf 0x7fffffff
using namespace std;
typedef long long ll;
const int maxn=1111;
int n,m,from,to;
struct node
{
    int v,flow,cost;
    int next;
} edge[maxn*40];
int head[maxn],edgenum;
ll dis[maxn],pre[maxn],pid[maxn],vis[maxn];

int S[maxn],T[maxn],C[maxn][maxn],D[maxn][maxn],E[maxn][maxn],F[maxn][maxn];
void add(int u,int v,int flow,int cost)
{
    edge[edgenum].v=v ;
    edge[edgenum].flow=flow ;
    edge[edgenum].cost=cost ;
    edge[edgenum].next=head[u];
    head[u]=edgenum++;

    edge[edgenum].v=u ;
    edge[edgenum].flow=0;
    edge[edgenum].cost=-cost ;
    edge[edgenum].next=head[v];
    head[v]=edgenum++;
}

ll spfa()
{
    for (int i=0 ; i<=to ; i++)
    {
        dis[i]=inf;
        vis[i]=0;
    }
    queue<int> Q;
    Q.push(from);
    dis[from]=0;
    vis[from]=1;
    while (!Q.empty())
    {
        int u=Q.front() ;
        Q.pop() ;
        vis[u]=0;
        for (int i=head[u] ; i!=-1 ; i=edge[i].next)
        {
            int v=edge[i].v;
            if (edge[i].flow>0 && dis[v]>dis[u]+edge[i].cost)
            {
                dis[v]=dis[u]+edge[i].cost;
                pre[v]=u;
                pid[v]=i;
                if (!vis[v])
                {
                    vis[v]=1;
                    Q.push(v);
                }
            }
        }
    }
    return dis[to];
}

int mincost()
{
    int aug=0,maxflow=0;
    ll ans=0,tmp=0;
    while (1)
    {
        tmp=spfa();
        if (tmp==inf) break;
        aug=inf;
        for (int i=to ; i!=from ; i=pre[i])
        {
            if (edge[pid[i] ].flow<aug)
                aug=edge[pid[i] ].flow;
        }
        for (int i=to ; i!=from ; i=pre[i])
        {
            edge[pid[i] ].flow -= aug;
            edge[pid[i]^1 ].flow += aug;
        }
        maxflow += aug;
        ans += tmp;
        //printf("%d ",ans);
    }
    if(maxflow!=n)
        printf("-1\n");
    else
        printf("%I64d\n",ans);
}

int main()
{
    int k;
    while (scanf("%d%d%d",&n,&m,&k)!=EOF&&(n+m+k))
    {
        memset(head,-1,sizeof(head));
        edgenum=0;
        for(int i=0; i<n; i++)
        {
            scanf("%d%d",&S[i],&T[i]);
        }
        for(int i=0; i<n; i++)
            for(int j=0; j<m; j++)
                scanf("%d",&C[i][j]);
        for(int i=0; i<n; i++)
            for(int j=0; j<m; j++)
                scanf("%d",&D[i][j]);
        for(int i=0; i<n; i++)
            for(int j=0; j<n; j++)
                scanf("%d",&E[i][j]);
        for(int i=0; i<n; i++)
            for(int j=0; j<n; j++)
                scanf("%d",&F[i][j]);
        from=0;
        to=n*2+m+1;
        for(int i=0; i<m; i++)
        {
            add(0,i+1,1,0);
        }
        for(int i=0; i<n; i++)
        {
            add(0,i+1+m,1,0);
            add(i+1+m+n,to,1,0);
        }
        for(int i=0; i<m; i++)
        {
            for(int j=0; j<n; j++)
            {
                if(S[j]>C[j][i])
                    add(i+1,n+m+j+1,1,D[j][i]);
                else if(T[j]>C[j][i])
                    add(i+1,n+m+j+1,1,D[j][i]+k*(C[j][i]-S[j]));
            }
        }
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<n; j++)
                if(i!=j)
                {
                    if(T[i]+E[i][j]<T[j])
                    {
                        if(S[j]>E[i][j]+T[i])
                            add(i+1+m,m+j+1+n,1,F[i][j]);
                        else
                            add(i+1+m,m+j+1+n,1,F[i][j]+k*(T[i]+E[i][j]-S[j]));
                    }
                }
        }
        mincost();
    }
    return 0;
}