递归算法是《数据结构与算法》中最简洁的算法之一,它可以非常简明地描述“减而治之”(decrease and conquer)和“分而治之”(divide and conquer)这两种算法思想。递归算法虽然从代码角度来看非常简单,但对于新手理解起来却不那么简单。本文我将结合《数据结构与算法》的专业描述和《程序员的数学》的通俗描述,并以“汉诺塔”为例来讲解我对“递归”算法的理解,并给出 Python 代码描述。
一、汉诺塔迷题
“汉诺塔”是由数学家 Edouard Lucas 于1883 年发明的游戏,具体内容可以看 wiki - 汉诺塔 ,下面给出 3 层汉诺塔的移动示意图:
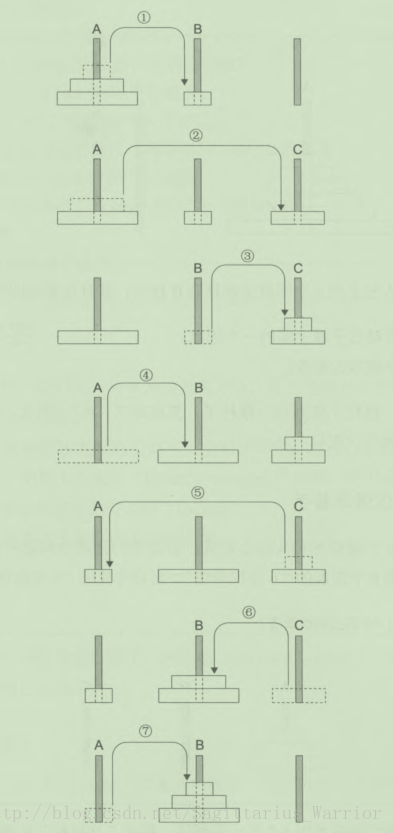
从上图可以观察到,过程 1、2、3 和过程 5、6、7是非常相似的,前者将 2 个圆盘从 A 移到 C ;后者将 2 个圆盘从 C 移到 B 。总结如下:
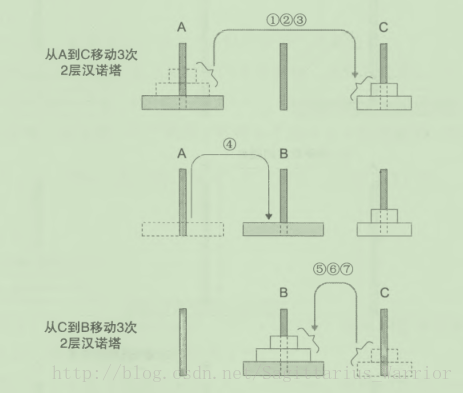
二、递归思维
从上面对“汉诺塔”迷题的观察和分析可以清楚的反映“递归”的思维方式:当我们碰到“简单问题易解(一层汉诺塔),复杂问题难解(多层汉诺塔)”时,尝试问自己“能将复杂的问题转化为较为简单的同类问题吗?”
这就是递归的思维方式,对于汉诺塔来说,就是将 n 层汉诺塔转换为 n-1 层汉诺塔问题,即在问题中找出递归结构。
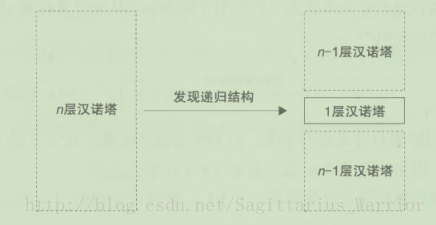
如果找到了递归结构,接下来就是根据递归结构建立递归公式
{








 本文通过汉诺塔问题深入浅出地解析了递归算法的思维方式和实现,详细介绍了如何从复杂问题中找出递归结构,并提供了Python代码实现。递归算法的关键在于递归基和递推公式,通过分析汉诺塔问题,展示了如何通过递归解决此类问题。
本文通过汉诺塔问题深入浅出地解析了递归算法的思维方式和实现,详细介绍了如何从复杂问题中找出递归结构,并提供了Python代码实现。递归算法的关键在于递归基和递推公式,通过分析汉诺塔问题,展示了如何通过递归解决此类问题。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1110
1110

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








