阅读本文需要的背景知识点:一丢丢编程知识
一、引言
在生活中,每次到饭点时都会在心里默念——“等下吃啥?”,可能今天工作的一天了不想走远了,这时我们会决定餐厅的距离不能超过两百米,再看看自己钱包里的二十块钱,决定吃的东西不能超过二十,最后点了份兰州拉面。从上面的例子中可以看到,我们今天吃兰州拉面都是由前面一系列的决策所决定的。

如图1-1 所示,将上面的决策过程用一颗二叉树来表示,这个树就被称为决策树(Decision Tree)。在机器学习中,同样可以通过数据集训练出如图1-1所示的决策树模型,这种算法被称为决策树学习算法(Decision Tree Learning)1 。
二、模型介绍
模型
决策树学习算法(Decision Tree Learning),首先肯定是一个树状结构,由内部结点与叶子结点组成,内部结点表示一个维度(特征),叶子结点表示一个分类。结点与结点之间通过一定的条件相连接,所以决策树又可以看成一堆if…else…规则的集合。

如图2-1 所示,其展示了一颗基本的决策树数据结构与其包含的决策方法。
特征选择
既然要做决策,需要决定的就是从哪个维度(特征)来做决策,例如前面例子中的店铺距离、钱包零钱数等。在机器学习中我们需要一个量化的指标来确定使用的特征更加合适,即使用该特征划分后,得到的子集合的“纯度”更高。这时引入三种指标——信息增益(Information Gain)、基尼指数(Gini Index)、均方误差(MSE)来解决前面说的问题。
信息增益(Information Gain)
式2-1 是一种表示样本集纯度的指标,被称为信息熵(Information Entropy),其中 D 表示样本集, K 表示样本集分类数,
p
k
p_k
pk 表示第 k 类样本在样本集所占比例。Ent(D) 的值越小,样本集的纯度越高。
Ent
(
D
)
=
−
∑
k
=
1
K
p
k
log
2
p
k
\operatorname{Ent}(D)=-\sum_{k=1}^{K} p_{k} \log _{2} p_{k}
Ent(D)=−k=1∑Kpklog2pk
式2-2 表示用一个离散属性划分后对样本集的影响,被称为信息增益(Information Gain),其中 D 表示样本集,a 表示离散属性,V 表示离散属性 a 所有可能取值的数量,
D
v
D^v
Dv 表示样本集中第 v 种取值的子样本集。
Gain
(
D
,
a
)
=
Ent
(
D
)
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
Ent
(
D
v
)
\operatorname{Gain}(D, a)=\operatorname{Ent}(D)-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right)
Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
当属性是连续属性时,其可取值不像离散属性那样是有限的,这时可以将连续属性在样本集中的值排序后俩俩取平均值作为划分点,改写一下式2-2,得到如式2-3 的结果,其中
T
a
T_a
Ta 表示平均值集合,
D
t
v
D_t^v
Dtv 表示子集合,当 v = - 时表示样本中小于均值 t 的样本子集,当 v = + 时表示样本中大于均值t的样本子集,取划分点中最大的信息增益作为该属性的信息增益值。
T
a
=
{
a
i
+
a
i
+
1
2
∣
1
≤
i
≤
n
−
1
}
Gain
(
D
,
a
)
=
max
t
∈
T
a
Gain
(
D
,
a
,
t
)
=
max
t
∈
T
a
Ent
(
D
)
−
∑
v
∈
{
−
,
+
}
∣
D
t
v
∣
∣
D
∣
Ent
(
D
t
v
)
\begin{aligned} T_{a} &=\left\{\frac{a^{i}+a^{i+1}}{2} \mid 1 \leq i \leq n-1\right\} \\ \operatorname{Gain}(D, a) &=\max _{t \in T_{a}} \operatorname{Gain}(D, a, t) \\ &=\max _{t \in T_{a}} \operatorname{Ent}(D)-\sum_{v \in\{-,+\}} \frac{\left|D_{t}^{v}\right|}{|D|} \operatorname{Ent}\left(D_{t}^{v}\right) \end{aligned}
TaGain(D,a)={2ai+ai+1∣1≤i≤n−1}=t∈TamaxGain(D,a,t)=t∈TamaxEnt(D)−v∈{−,+}∑∣D∣∣Dtv∣Ent(Dtv)
Gain(D, a) 的值越大,样本集按该属性划分后纯度的提升越高。由此可找到最合适的划分属性,如式2-4 所示:
a
best
=
argmax
a
Gain
(
D
,
a
)
a_{\text {best }}=\underset{a}{\operatorname{argmax}} \operatorname{Gain}(D, a)
abest =aargmaxGain(D,a)
基尼指数(Gini Index)
式2-5 是另一种表示样本集纯度的指标,被称为基尼值(Gini),其中 D 表示样本集, K 表示样本集分类数,
p
k
p_k
pk 表示第 k 类样本在样本集所占比例。Gini(D) 的值越小,样本集的纯度越高。
Gini
(
D
)
=
1
−
∑
k
=
1
K
p
k
2
\operatorname{Gini}(D)=1-\sum_{k=1}^{K} p_{k}^{2}
Gini(D)=1−k=1∑Kpk2
式2-6 表示用一个离散属性划分后对样本集的影响,被称为基尼指数(Gini Index),其中 D 表示样本集,a 表示离散属性,V 表示离散属性 a 所有可能取值的数量,
D
v
D^v
Dv 表示样本集中第 v 种取值的子样本集。
G
i
n
i
−
i
n
d
e
x
(
D
,
a
)
=
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
Gini
(
D
v
)
\operatorname{Gini_{-}index}(D, a)=\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Gini}\left(D^{v}\right)
Gini−index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)
同式2-3一样,将连续属性排序后俩俩取平均值作为划分点,改写式2-6,得到如式2-7 的结果,其中
T
a
T_a
Ta 表示平均值集合,
D
t
v
D_t^v
Dtv 表示子集合,当 v = - 时表示样本中小于均值 t 的样本子集,当 v = + 时表示样本中大于均值 t 的样本子集,取划分点中最小的基尼指数作为该属性的基尼指数值。
G
i
n
i
−
i
n
d
e
x
(
D
,
a
)
=
min
t
∈
T
a
∑
v
∈
{
−
,
+
}
∣
D
t
v
∣
∣
D
∣
Gini
(
D
t
v
)
\operatorname{Gini_{-}index}(D, a)=\min _{t \in T_{a}} \sum_{v \in\{-,+\}} \frac{\left|D_{t}^{v}\right|}{|D|} \operatorname{Gini}\left(D_{t}^{v}\right)
Gini−index(D,a)=t∈Taminv∈{−,+}∑∣D∣∣Dtv∣Gini(Dtv)
Gini_index(D, a) 的值越小,样本集按该离散属性划分后纯度的提升越高。由此可找到最合适的划分属性,如式2-8所示:
a
best
=
argmin
a
Gini_index
(
D
,
a
)
a_{\text {best }}=\underset{a}{\operatorname{argmin}} \operatorname{Gini\_index}(D, a)
abest =aargminGini_index(D,a)
均方误差(MSE)
前面两种指标使得决策树可以用来做分类问题,那么决策树如果用来做回归问题时,就需要不同的指标来决定划分的特征,这个指标就是如式2-9 所示的均方误差(MSE),其中
T
a
T_a
Ta 表示平均值集合,
y
t
v
y_t^v
ytv 表示子集合标签,当 v = - 时表示样本中小于均值 t 的样本子集标签,当 v = + 时表示样本中大于均值 t 的样本子集标签,后一项为对应子集合标签的均值。
MSE
(
D
,
a
)
=
min
t
∈
T
a
∑
v
∈
{
−
,
+
}
(
y
t
v
−
y
t
v
^
)
2
\operatorname{MSE}(D, a)=\min _{t \in T_{a}} \sum_{v \in\{-,+\}}\left(y_{t}^{v}-\hat{y_{t}^{v}}\right)^{2}
MSE(D,a)=t∈Taminv∈{−,+}∑(ytv−ytv^)2
MSE(D, a) 的值越小,决策树对样本集的拟合程度越高。由此可找到最合适的划分属性,如式2-10 所示:
a
best
=
argmin
a
MSE
(
D
,
a
)
a_{\text {best }}=\underset{a}{\operatorname{argmin}} \operatorname{MSE}(D, a)
abest =aargminMSE(D,a)
知道了决策树模型的数据结构,又知道如何划分最佳的数据集,那么接下来就来学习如何生成一颗决策树。
三、算法步骤
既然决策树的数据结构是一颗树,其子结点也必然是一颗树,可以通过递归的方式来生成决策树,步骤如下:
生成新结点 node;
当样本中只存在一种分类C时:
将结点 node 标记为分类C的叶子结点,返回结点 node;
遍历所有特征:
计算当前特征的信息增益或基尼指数或均方误差;
结点 node 中记录最佳的划分特征;
按照最佳特征划分后左边部分递归调用当前方法,当作结点 node 的左子结点;
按照最佳特征划分后右边部分递归调用当前方法,当作结点 node 的右子结点;
返回结点 node;
四、正则化
当递归的生成决策树时,模型对训练数据的分类会非常准确,但是对未知的预测数据的表现并不理想,这就是所谓的过拟合的现象,这时可以同前面线性回归学习到的应对过拟合的解决方法一样,对模型进行正则化。
决策树的深度
可以通过限制决策树的最大深度来达到对其正则化的效果,防止决策树过拟合。这时只需在算法步骤中加上一个用于记录当前递归下树深度的参数,当到达预设的最大深度时,不再生成新的子结点,将当前结点标记为样本中分类占比最大的分类并退出当前递归。
决策树的叶子结点大小
另一个对决策树进行正则化的方法是限制叶子结点最少包含的样本数量,同样可以防止过拟合的现象。当结节包含的样本数,将当前结点标记为样本中分类占比最大的分类并退出当前递归
决策树的剪枝
还可以通过对决策树进行剪枝来防止其过拟合,将多余的子树剪断。剪枝的方法又分成两种,分别为预剪枝(prepruning)、后剪枝(post-pruning)。
预剪枝
顾名思义,预剪枝就是在生成决策树的时候就决定是否生成子结点,判断的方法为使用验证数据集比较生成子结点与不生成子结点的精度,当生成子结点的精度有提升,则生成子结点,反之则不生成子结点。
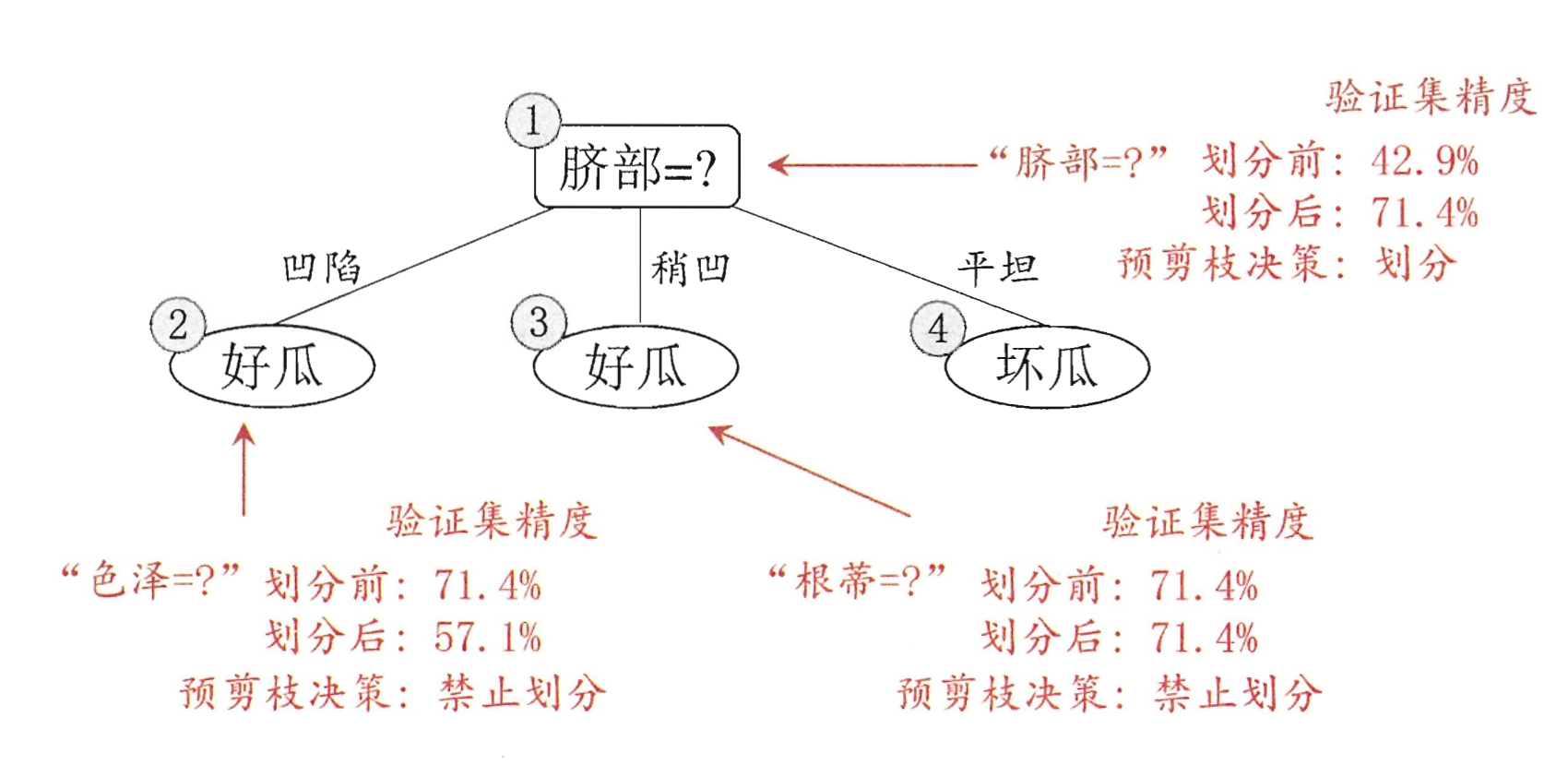
后剪枝
后剪枝则是先生成一个完整的决策树,然后再从叶子结点开始,同预剪枝一样的判断方法,当生成子结点的精度有提升,则保留子结点,反之则将子结点剪断。

五、代码实现
使用 Python 实现基于信息增益的决策树分类:
import numpy as np
class GainNode:
"""
分类决策树中的结点
基于信息增益-Information Gain
"""
def __init__(self, feature=None, threshold=None, gain=None, left=None, right=None):
# 结点划分的特征下标
self.feature = feature
# 结点划分的临界值,当结点为叶子结点时为分类值
self.threshold = threshold
# 结点的信息增益值
self.gain = gain
# 左结点
self.left = left
# 右结点
self.right = right
class GainTree:
"""
分类决策树
基于信息增益-Information Gain
"""
def __init__(self, max_depth = None, min_samples_leaf = None):
# 决策树最大深度
self.max_depth = max_depth
# 决策树叶结点最小样本数
self.min_samples_leaf = min_samples_leaf
def fit(self, X, y):
"""
分类决策树拟合
基于信息增益-Information Gain
"""
y = np.array(y)
self.root = self.buildNode(X, y, 0)
return self
def buildNode(self, X, y, depth):
"""
构建分类决策树结点
基于信息增益-Information Gain
"""
node = GainNode()
# 当没有样本时直接返回
if len(y) == 0:
return node
y_classes = np.unique(y)
# 当样本中只存在一种分类时直接返回该分类
if len(y_classes) == 1:
node.threshold = y_classes[0]
return node
# 当决策树深度达到最大深度限制时返回样本中分类占比最大的分类
if self.max_depth is not None and depth >= self.max_depth:
node.threshold = max(y_classes, key=y.tolist().count)
return node
# 当决策树叶结点样本数达到最小样本数限制时返回样本中分类占比最大的分类
if self.min_samples_leaf is not None and len(y) <= self.min_samples_leaf:
node.threshold = max(y_classes, key=y.tolist().count)
return node
max_gain = -np.inf
max_middle = None
max_feature = None
# 遍历所有特征,获取信息增益最大的特征
for i in range(X.shape[1]):
# 计算特征的信息增益
gain, middle = self.calcGain(X[:,i], y, y_classes)
if max_gain < gain:
max_gain = gain
max_middle = middle
max_feature = i
# 信息增益最大的特征
node.feature = max_feature
# 临界值
node.threshold = max_middle
# 信息增益
node.gain = max_gain
X_lt = X[:,max_feature] < max_middle
X_gt = X[:,max_feature] > max_middle
# 递归处理左集合
node.left = self.buildNode(X[X_lt,:], y[X_lt], depth + 1)
# 递归处理右集合
node.right = self.buildNode(X[X_gt,:], y[X_gt], depth + 1)
return node
def calcMiddle(self, x):
"""
计算连续型特征的俩俩平均值
"""
middle = []
if len(x) == 0:
return np.array(middle)
start = x[0]
for i in range(len(x) - 1):
if x[i] == x[i + 1]:
continue
middle.append((start + x[i + 1]) / 2)
start = x[i + 1]
return np.array(middle)
def calcEnt(self, y, y_classes):
"""
计算信息熵
"""
ent = 0
for j in range(len(y_classes)):
p = len(y[y == y_classes[j]])/ len(y)
if p != 0:
ent = ent + p * np.log2(p)
return -ent
def calcGain(self, x, y, y_classes):
"""
计算信息增益
"""
x_sort = np.sort(x)
middle = self.calcMiddle(x_sort)
max_middle = -np.inf
max_gain = -np.inf
ent = self.calcEnt(y, y_classes)
# 遍历每个平均值
for i in range(len(middle)):
y_gt = y[x > middle[i]]
y_lt = y[x < middle[i]]
ent_gt = self.calcEnt(y_gt, y_classes)
ent_lt = self.calcEnt(y_lt, y_classes)
# 计算信息增益
gain = ent - (ent_gt * len(y_gt) / len(x) + ent_lt * len(y_lt) / len(x))
if max_gain < gain:
max_gain = gain
max_middle = middle[i]
return max_gain, max_middle
def predict(self, X):
"""
分类决策树预测
"""
y = np.zeros(X.shape[0])
self.checkNode(X, y, self.root)
return y
def checkNode(self, X, y, node, cond = None):
"""
通过分类决策树结点判断分类
"""
# 当没有子结点时,直接返回当前临界值
if node.left is None and node.right is None:
return node.threshold
X_lt = X[:,node.feature] < node.threshold
if cond is not None:
X_lt = X_lt & cond
# 递归判断左结点
lt = self.checkNode(X, y, node.left, X_lt)
if lt is not None:
y[X_lt] = lt
X_gt = X[:,node.feature] > node.threshold
if cond is not None:
X_gt = X_gt & cond
# 递归判断右结点
gt = self.checkNode(X, y, node.right, X_gt)
if gt is not None:
y[X_gt] = gt
使用 Python 实现基于基尼指数的决策树分类:
import numpy as np
class GiniNode:
"""
分类决策树中的结点
基于基尼指数-Gini Index
"""
def __init__(self, feature=None, threshold=None, gini_index=None, left=None, right=None):
# 结点划分的特征下标
self.feature = feature
# 结点划分的临界值,当结点为叶子结点时为分类值
self.threshold = threshold
# 结点的基尼指数值
self.gini_index = gini_index
# 左结点
self.left = left
# 右结点
self.right = right
class GiniTree:
"""
分类决策树
基于基尼指数-Gini Index
"""
def __init__(self, max_depth = None, min_samples_leaf = None):
# 决策树最大深度
self.max_depth = max_depth
# 决策树叶结点最小样本数
self.min_samples_leaf = min_samples_leaf
def fit(self, X, y):
"""
分类决策树拟合
基于基尼指数-Gini Index
"""
y = np.array(y)
self.root = self.buildNode(X, y, 0)
return self
def buildNode(self, X, y, depth):
"""
构建分类决策树结点
基于基尼指数-Gini Index
"""
node = GiniNode()
# 当没有样本时直接返回
if len(y) == 0:
return node
y_classes = np.unique(y)
# 当样本中只存在一种分类时直接返回该分类
if len(y_classes) == 1:
node.threshold = y_classes[0]
return node
# 当决策树深度达到最大深度限制时返回样本中分类占比最大的分类
if self.max_depth is not None and depth >= self.max_depth:
node.threshold = max(y_classes, key=y.tolist().count)
return node
# 当决策树叶结点样本数达到最小样本数限制时返回样本中分类占比最大的分类
if self.min_samples_leaf is not None and len(y) <= self.min_samples_leaf:
node.threshold = max(y_classes, key=y.tolist().count)
return node
min_gini_index = np.inf
min_middle = None
min_feature = None
# 遍历所有特征,获取基尼指数最小的特征
for i in range(X.shape[1]):
# 计算特征的基尼指数
gini_index, middle = self.calcGiniIndex(X[:,i], y, y_classes)
if min_gini_index > gini_index:
min_gini_index = gini_index
min_middle = middle
min_feature = i
# 基尼指数最小的特征
node.feature = min_feature
# 临界值
node.threshold = min_middle
# 基尼指数
node.gini_index = min_gini_index
X_lt = X[:,min_feature] < min_middle
X_gt = X[:,min_feature] > min_middle
# 递归处理左集合
node.left = self.buildNode(X[X_lt,:], y[X_lt], depth + 1)
# 递归处理右集合
node.right = self.buildNode(X[X_gt,:], y[X_gt], depth + 1)
return node
def calcMiddle(self, x):
"""
计算连续型特征的俩俩平均值
"""
middle = []
if len(x) == 0:
return np.array(middle)
start = x[0]
for i in range(len(x) - 1):
if x[i] == x[i + 1]:
continue
middle.append((start + x[i + 1]) / 2)
start = x[i + 1]
return np.array(middle)
def calcGiniIndex(self, x, y, y_classes):
"""
计算基尼指数
"""
x_sort = np.sort(x)
middle = self.calcMiddle(x_sort)
min_middle = np.inf
min_gini_index = np.inf
for i in range(len(middle)):
y_gt = y[x > middle[i]]
y_lt = y[x < middle[i]]
gini_gt = self.calcGini(y_gt, y_classes)
gini_lt = self.calcGini(y_lt, y_classes)
gini_index = gini_gt * len(y_gt) / len(x) + gini_lt * len(y_lt) / len(x)
if min_gini_index > gini_index:
min_gini_index = gini_index
min_middle = middle[i]
return min_gini_index, min_middle
def calcGini(self, y, y_classes):
"""
计算基尼值
"""
gini = 1
for j in range(len(y_classes)):
p = len(y[y == y_classes[j]])/ len(y)
gini = gini - p * p
return gini
def predict(self, X):
"""
分类决策树预测
"""
y = np.zeros(X.shape[0])
self.checkNode(X, y, self.root)
return y
def checkNode(self, X, y, node, cond = None):
"""
通过分类决策树结点判断分类
"""
if node.left is None and node.right is None:
return node.threshold
X_lt = X[:,node.feature] < node.threshold
if cond is not None:
X_lt = X_lt & cond
lt = self.checkNode(X, y, node.left, X_lt)
if lt is not None:
y[X_lt] = lt
X_gt = X[:,node.feature] > node.threshold
if cond is not None:
X_gt = X_gt & cond
gt = self.checkNode(X, y, node.right, X_gt)
if gt is not None:
y[X_gt] = gt
使用 Python 实现基于均方误差的决策树回归:
import numpy as np
class RegressorNode:
"""
回归决策树中的结点
"""
def __init__(self, feature=None, threshold=None, mse=None, left=None, right=None):
# 结点划分的特征下标
self.feature = feature
# 结点划分的临界值,当结点为叶子结点时为分类值
self.threshold = threshold
# 结点的均方误差值
self.mse = mse
# 左结点
self.left = left
# 右结点
self.right = right
class RegressorTree:
"""
回归决策树
"""
def __init__(self, max_depth = None, min_samples_leaf = None):
# 决策树最大深度
self.max_depth = max_depth
# 决策树叶结点最小样本数
self.min_samples_leaf = min_samples_leaf
def fit(self, X, y):
"""
回归决策树拟合
"""
self.root = self.buildNode(X, y, 0)
return self
def buildNode(self, X, y, depth):
"""
构建回归决策树结点
"""
node = RegressorNode()
# 当没有样本时直接返回
if len(y) == 0:
return node
y_classes = np.unique(y)
# 当样本中只存在一种分类时直接返回该分类
if len(y_classes) == 1:
node.threshold = y_classes[0]
return node
# 当决策树深度达到最大深度限制时返回样本中分类占比最大的分类
if self.max_depth is not None and depth >= self.max_depth:
node.threshold = np.average(y)
return node
# 当决策树叶结点样本数达到最小样本数限制时返回样本中分类占比最大的分类
if self.min_samples_leaf is not None and len(y) <= self.min_samples_leaf:
node.threshold = np.average(y)
return node
min_mse = np.inf
min_middle = None
min_feature = None
# 遍历所有特征,获取均方误差最小的特征
for i in range(X.shape[1]):
# 计算特征的均方误差
mse, middle = self.calcMse(X[:,i], y)
if min_mse > mse:
min_mse = mse
min_middle = middle
min_feature = i
# 均方误差最小的特征
node.feature = min_feature
# 临界值
node.threshold = min_middle
# 均方误差
node.mse = min_mse
X_lt = X[:,min_feature] < min_middle
X_gt = X[:,min_feature] > min_middle
# 递归处理左集合
node.left = self.buildNode(X[X_lt,:], y[X_lt], depth + 1)
# 递归处理右集合
node.right = self.buildNode(X[X_gt,:], y[X_gt], depth + 1)
return node
def calcMiddle(self, x):
"""
计算连续型特征的俩俩平均值
"""
middle = []
if len(x) == 0:
return np.array(middle)
start = x[0]
for i in range(len(x) - 1):
if x[i] == x[i + 1]:
continue
middle.append((start + x[i + 1]) / 2)
start = x[i + 1]
return np.array(middle)
def calcMse(self, x, y):
"""
计算均方误差
"""
x_sort = np.sort(x)
middle = self.calcMiddle(x_sort)
min_middle = np.inf
min_mse = np.inf
for i in range(len(middle)):
y_gt = y[x > middle[i]]
y_lt = y[x < middle[i]]
avg_gt = np.average(y_gt)
avg_lt = np.average(y_lt)
mse = np.sum((y_lt - avg_lt) ** 2) + np.sum((y_gt - avg_gt) ** 2)
if min_mse > mse:
min_mse = mse
min_middle = middle[i]
return min_mse, min_middle
def predict(self, X):
"""
回归决策树预测
"""
y = np.zeros(X.shape[0])
self.checkNode(X, y, self.root)
return y
def checkNode(self, X, y, node, cond = None):
"""
通过回归决策树结点判断分类
"""
if node.left is None and node.right is None:
return node.threshold
X_lt = X[:,node.feature] < node.threshold
if cond is not None:
X_lt = X_lt & cond
lt = self.checkNode(X, y, node.left, X_lt)
if lt is not None:
y[X_lt] = lt
X_gt = X[:,node.feature] > node.threshold
if cond is not None:
X_gt = X_gt & cond
gt = self.checkNode(X, y, node.right, X_gt)
if gt is not None:
y[X_gt] = gt
六、第三方库实现
scikit-learn2 决策树分类实现
from sklearn import tree
# 决策树分类
clf = tree.DecisionTreeClassifier()
# 拟合数据
clf = clf.fit(X, y)
scikit-learn3 决策树回归实现
from sklearn import tree
# 决策树回归
clf = tree.DecisionTreeRegressor()
# 拟合数据
clf = clf.fit(X, y)
七、示例演示
图7-1 展示了一颗未进行正则化的决策树的分类结果,图7-2 展示了一颗正则化后的决策树(max_depth = 3, min_samples_leaf = 5)的分类结果

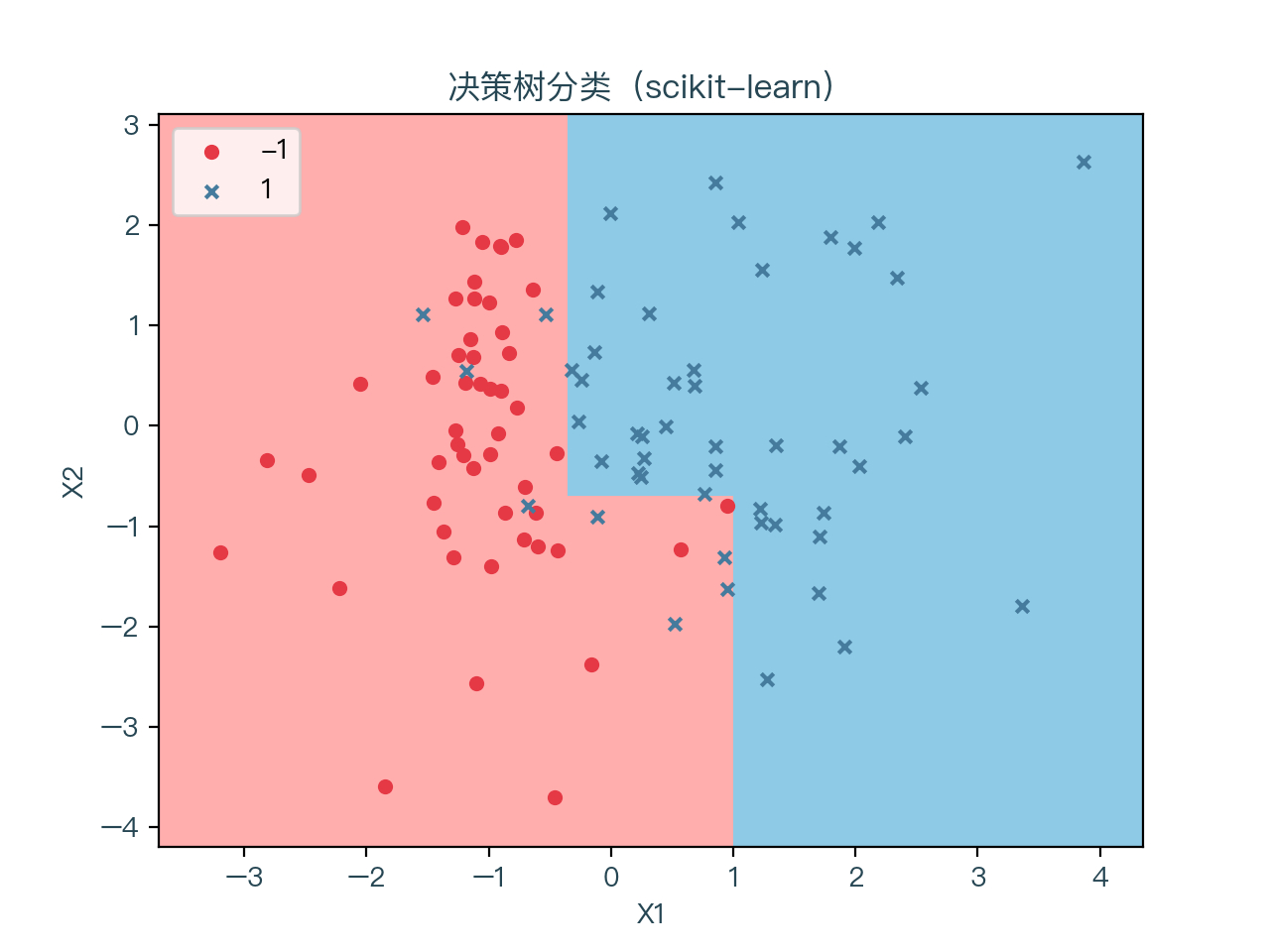
图7-3 展示了一颗未进行正则化的决策树的回归结果,图7-4 展示了一颗正则化后的决策树(max_depth = 3, min_samples_leaf = 5)的回归结果


可以看到未进行正则化的决策树对训练数据集明显过拟合,进行正则化后的决策树的情况相对好一些。
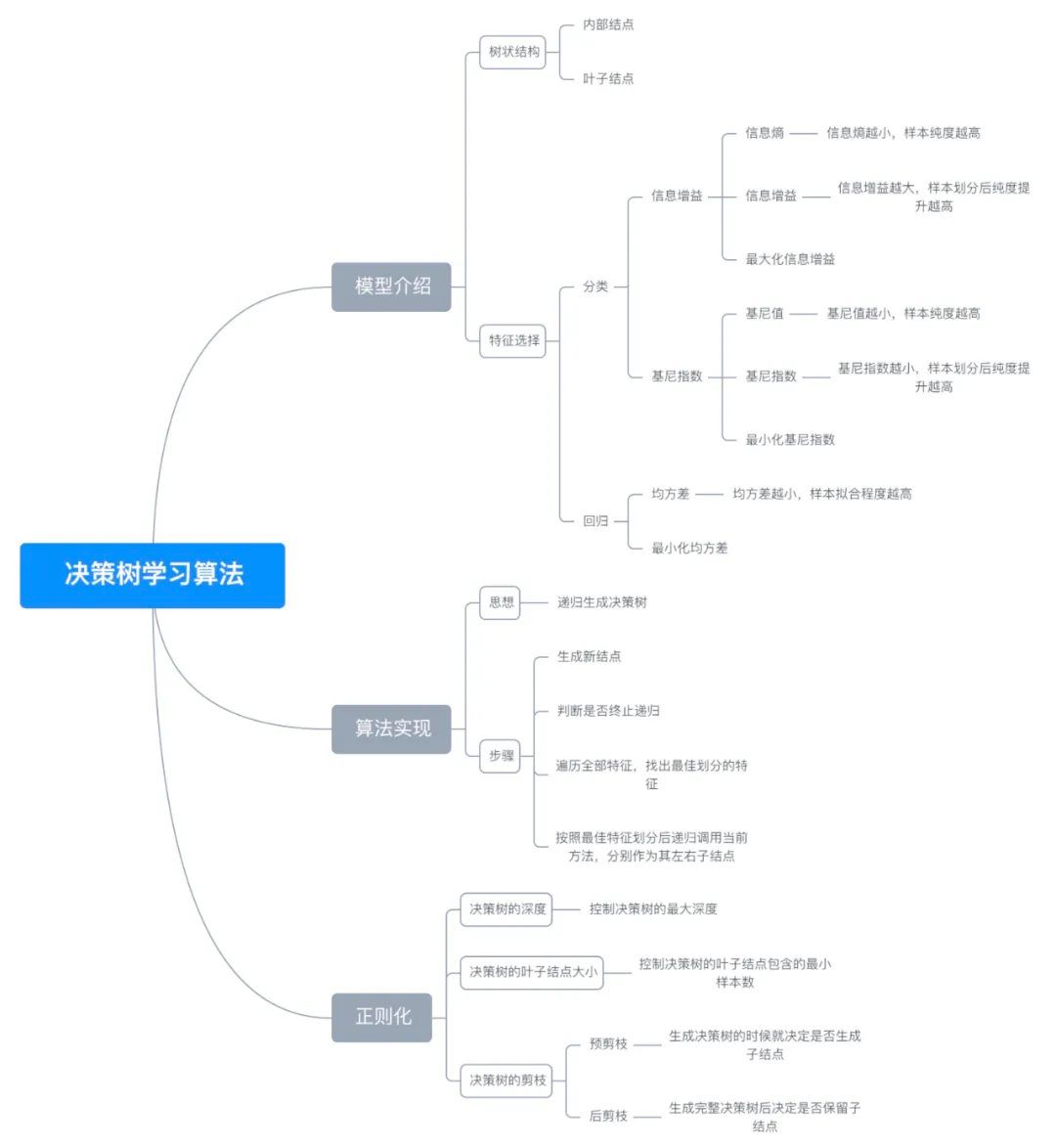
八、思维导图
九、参考文献
- https://en.wikipedia.org/wiki/Decision_tree_learning
- https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html
- https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html
完整演示请点击这里
注:本文力求准确并通俗易懂,但由于笔者也是初学者,水平有限,如文中存在错误或遗漏之处,恳请读者通过留言的方式批评指正
本文首发于——AI导图,欢迎关注
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








