密码学原理精解【3】

希尔密码

矩阵

矩阵基本概念

• 在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。

• 由 m × n 个数$a_{ij}$排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。
  $$A=\left[\begin{array}{cccc}{A}_{11}& A_{12}& ...& A_{1n}\\ A_{21}& A_{22}& ...& A_{2n}\\ ...& ...& ...& ...\\ A_{m1}& A_{m2}& ...& A_{mn}\end{array}\right]$$

• m×n 个数称为矩阵A的元素，简称为元。

• 数$a_{ij}$位于矩阵A的第i行第j列，称为矩阵A的$(i,j)$元

• m×n矩阵A也记作$A_{mn}$。

• 元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。

• 行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。

• 特征值与特征向量:
  n×n的方块矩阵A的一个特征值和对应特征向量是满足$Av=\lambda v$的标量以及非零向量。其中$v$为特征向量，$\lambda$为特征值。
  线性变换的特征向量是指在变换下方向不变，或者简单地乘以一个缩放因子的非零向量。
  特征向量对应的特征值是它所乘的那个缩放因子。

行列式基本概念

一个n×n的正方矩阵A的行列式记为$det(A)$或$|A|$，行列式的值仅仅是一个数，不是矩阵之类的。

• 2×2矩阵的行列式计算方式如下：
  $$det\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)=ad-cb$$

• 元素$a_{ij}$的代数余子式
  (1)在n阶行列式中，把元素$a_{ij}$所在的第i行和第j列划去后，留下来的n-1阶行列式叫做元素$a_{ij}$的余子式，记作$M_{ij}$。
  (2)将余子式$M_{ij}$再乘以-1的i+j次幂记为$A_{ij}。$即： $A_{ij}=(-1{)}^{i+j}{M}_{ij}$
  (3)$A_{ij}$叫做元素$a_{ij}$的代数余子式。
  (4)一个元素$a_{ij}$的代数余子式与该元素本身没什么关系，只与该元素的位置有关。

• 计算行列式值
  n×n矩阵的行列式计算方式如下：
  其任意行（或列）的元素与对应的代数余子式乘积之和
  $$\begin{gathered} A=\left[\begin{array}{cccc}{A}_{11}& A_{12}& ...& A_{1n}\\ A_{21}& A_{22}& ...& A_{2n}\\ ...& ...& ...& ...\\ A_{n1}& A_{n2}& ...& A_{nn}\end{array}\right] \\ det(A)=|A|=a_{i1}{A}_{i1}+...+a_{in}{A}_{in}=\sum _{j=1}^n{a}_{ij}det(A_{ij}) \\ 即：行列式等于它的任一行(列)的所有元素与其对应的代数余子式的乘积之和 \end{gathered}$$

• 两个性质
  $$\begin{gathered} det(I_m)=1 \\ det(AB)=det(A)det(B) \end{gathered}$$

特殊矩阵关于乘法运算构成群

1、$A_{lm}$$B_{mn}=C_{ln}$
$c_{i,k}={\sum }_{j=1}^m{a}_{i,j}{b}_{j,k},1\le i\le l,1\le k\le n$
2、$(AB)C=A(BC)$
3、一般矩阵不满足交换律$AB\ne BA$。
4、矩阵有单位矩阵（对角线为1，其余为0）$I_m=\left[\begin{array}{cccc}1& 0& ...& 0\\ 0& 1& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& 1\end{array}\right]$
其中，22矩阵$I_2=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$
$A{I}_m=A,I_{m}B=B$
5、如果A和B可逆
$A_{mm}{A}_{mm}^{-1}=A_{mm}^{-1}{A}_{mm}=I_m$
注意：可逆矩阵关于乘法运算不一定符合交换律，不一定构成交换群。
A怎么才能可逆呢?$det(A)\ne 0$则A可逆。
G L n ( R ) = { A ∈ M n ( R ) ∣ d e t ( A ) ≠ 0 } GL_n(R)=\{A \in M_n(R)|det(A)\not =0\} GLn​(R)={A∈Mn​(R)∣det(A)=0}，即所有n阶可逆实矩阵$G{L}_n(R)$关于矩阵乘法构成群。
6、伴随矩阵$A^{\ast }$
A各元素代数余子式$A_{ji}$组成伴随矩阵$A^{\ast }=(A_{ij})$

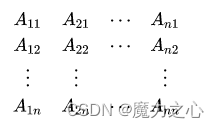
特别注意：i和j的顺序不一样，代数余子式$A_{ji}$在伴随矩阵中按列排列。

• 伴随矩阵$A^{\ast }$的一些基本性质
  （1）A可逆当且仅当$A^{\ast }$可逆。
  （2）如果A可逆，$A^{\ast }=|A|A^{-1}$
  $=>|A{|}^{-1}{A}^{\ast }=A^{-1}$

• R的逆元
  在R（实数）乘法群中
  $$\begin{gathered} 1为单位元。 \\ 设a\in R，a\ast \frac{1}{a}=1 \\ =>则a逆元a^{-1}为\frac{1}{a} \end{gathered}$$
  因此，$$\begin{gathered} |A{|}^{-1}=\frac{1}{|A|} \\ =>A^{-1}=A^{\ast }\frac{1}{|A|} \end{gathered}$$

• 二阶方阵可用下面方法求逆：
  $$\begin{gathered} A_{ij}为det(A)(也可写成|A|)中，元素a_{ij}的代数余子式。 \\ 当矩阵的阶数等于一阶时，伴随矩阵为一阶单位方阵。 \\ 二阶矩阵的伴随矩阵A^{\ast }求法口诀：主对角线元素互换，副对角线元素变号 \\ 伴随矩阵A^{\ast }=\left[\begin{array}{cc}{a}_{22}& -a_{12}\\ -a_{21}& a_{11}\end{array}\right] \\ {A}^{-1}=\frac{1}{|A|}{A}^{\ast } \end{gathered}$$

• 高阶矩阵可以用矩阵的初等行变换。
  在线性代数中，矩阵的初等行变换是指以下三种变换类型 ：
  $$\begin{gathered} (1)交换矩阵的两行（对调i,j，两行记为r_i，r_j）； \\ (2)以一个非零数k乘矩阵的某一行所有元素（第i行乘以k记为r_i\times k）； \\ (3)把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素(第j行乘以k加到第i行记为r_i+k\ast r_j)。 \end{gathered}$$

加解密原理

密钥

• 设m为正整数，P和C分别是原文和密文。
  $P=C=（Z_{26}{）}^m$
  这里的m为m维向量空间，m维欧氏空间的意思
  26即26个英文字母，也可以为$(Z_{256}{)}^m$（一个字节256个数字）
• 设m为2，即：每次对2个数字（即：2个英文字母或2个字节）进行加解密。
  明文：$x=(x_1,x_2)$，密文$y=(y_1,y_2)$
  $密钥:K=\left[\begin{array}{cc}{K}_{11}& K_{12}\\ K_{21}& K_{22}\end{array}\right]$
  特别注意：在$Z_{26}$或$Z_{256}$下进行运算。

加密函数

$$y_1=(x_1,x_2)\left[\begin{array}{cc}{k}_{11}& k_{12}\\ k_{21}& k_{22}\end{array}\right]mod26(或256)$$
特别注意上面函数是在$Z_{26}或Z_{256}下进行$
即：
$$\begin{gathered} y_1=(k_{11}{x}_1+k_{21}{x}_2)mod26(或256) \\ {y}_2=(k_{21}{x}_1+k_{22}{x}_2)mod26(或256) \end{gathered}$$

解密函数

$$\begin{gathered} y=xK \\ =>y{K}^{-1}=(xK)K^{-1}=x(K{K}^{-1})=x{I}_m=x \end{gathered}$$
$=>x=y{K}^{-1}$
特别注意上面函数是在$Z_{26}或Z_{256}下进行$

$Z_{26}上的运算（Z_{256}与此类似）$

• $|K{|}^{-1}=?$
  $$\begin{gathered} 这是错的：K^{-1}=\frac{1}{|K|}{K}^{\ast }，这不是在R乘法群，是在Z_{26}乘法群。 \\ {K}^{-1}=|K{|}^{-1}{K}^{\ast } \\ |K{|}^{-1}=? \end{gathered}$$

• $|K|=?$
  $$\begin{gathered} |K|=\sum _{j=1}^n{a}_{ij}(-1{)}^{i+j}det(A_{ij})，这也是错误的！！ \\ 这才是对的：|K|=\sum _{j=1}^n{a}_{ij}(-1{)}^{i+j}det(A_{ij})mod26 \\ 思考一下为什么？ \end{gathered}$$

• $K^{\ast }=?$
  $K_{ij}=(-1{)}^{i+j}{M}_{ij}$这也错了！？
  是的，错了！这只是在R乘法群的运算！

• $|K|\ne 0=>K可逆$
  这也是错误的，在$Z_{26}$中要变换如下：
  $gcd(|K|,26)=1=>K在Z_{26}可逆$

例1

$$\begin{gathered} 1、取K=\left[\begin{array}{cc}{K}_{11}& K_{12}\\ K_{21}& K_{22}\end{array}\right]=\left[\begin{array}{cc}19& 17\\ 2& 9\end{array}\right] \\ |K|=(19\ast 9-17\ast 2)mod26 \\ =137mod26=7 \\ =>gcd(7,26)=1 \\ =>K在Z_{26}中可逆。 \\ 2、7\ast 15\equiv 1(mod26)=>7^{-1}=15=>|K{|}^{-1}=15 \\ 3、K^{-1}=|K{|}^{-1}{A}^{\ast }=|K{|}^{-1}\left[\begin{array}{cc}{K}_{11}& -K_{12}\\ -K_{21}& K_{22}\end{array}\right]=15\left[\begin{array}{cc}9& -17\\ -2& 19\end{array}\right] \\ =15\left[\begin{array}{cc}9& 9\\ 24& 19\end{array}\right] \\ {K}^{-1}=\left[\begin{array}{cc}135& 135\\ 360& 285\end{array}\right]=\left[\begin{array}{cc}5& 5\\ 22& 25\end{array}\right] \\ 4、设原文x=(18,7) \\ (1)密文y=e_k(x)=xK=(18,7)\left[\begin{array}{cc}19& 17\\ 2& 9\end{array}\right] \\ =[356,359]=[18,5] \\ (2)原文x=d_k(y)=y{K}^{-1}=[18,5]\left[\begin{array}{cc}5& 5\\ 22& 25\end{array}\right] \\ =[200,215]=[18,7]=x \end{gathered}$$

关于负数取余问题：
1、当被除数能被除数整除时，无论被除数和除数的正负，余数都是0。
2、对于负数除以正数或，编译器会先将分子（即被除数的绝对值）转换为正整数进行取余运算。

参考文献

1、矩阵，百度百科
2、代数余子式，百度百科
3、特征向量，百度百科
4、《密码学原理与实践（第三版）》
5、矩阵变换，百度百科
6、伴随矩阵，百度百科