等额年金法总结

最新推荐文章于 2022-05-16 22:00:37 发布

Heisenberg_888

最新推荐文章于 2022-05-16 22:00:37 发布

阅读量6.5k

点赞数

分类专栏：财务管理（不务正业）

本文链接：https://blog.csdn.net/salmonwilliam/article/details/84980443

版权

财务管理（不务正业）专栏收录该内容

1 篇文章

订阅专栏

今天企业管理这门课遇到了等额年金法(等额年金在项目服务期内连续、等额发生在各期期末)，，总结一下：

什么是等额年金法

　　等额年金法指运用年金法，使各期租金均等的租金计算方法。

　　等额年金发生在(或折算为)某一特定时间序列各计息期末的等额序列。即从计算期的第一年至最后一年年末的效益额都相等时，称为等额年金。

等额年金法的类型

　　等额年金法分为先付和后付。

　　1）先付租金的等额年金法

　　在租金先付的情况下，等额年金法的计算公式为：

　　 $R=P_v\cdot\frac{i(1+i)^{n-1}}{(1+i)^n-1}$

　　2)后付租金的等额年金法

　　按照年金法计算的基本原理，后付租金的等额年金法的基本计算公式为：

　　 $R=P_v\cdot\frac{i(1+i)^n}{(1+i)^n-1}$

所谓现值是指在将来各个不同时期所支付的每一笔付款或一系列付款所折合的现金金额与现在支付的付款等值。现值是随远期付款的贴现利率变化而变化，如折现率为10％，一年以后的1000元，只相当现在的909.09元，这909.09元即为1000元将来货币的现值。现值的计算公式为：

　　 $P_v=S_n \times \frac{1}{(1+i)^n}$

　　其中：P_v为本金(现值)，i为复利率，n为复利次数，Sn为本利和(将来值/终值)

等额年金法计算公式的推导

　　1．期末后付租金复利定额年金法公式。根据现值计算公式，设R为每次(相同间隔)应付租金，P_v为租赁物件总成本，i为付租间隔期费率，n为付租次数，则，

　　第一次支付租金的现值为 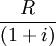$\frac{R}{(1+i)}$

　　第二次支付租金的现值为 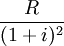$\frac{R}{(1+i)^2}$

　　......

　　第n-1次支付租金的现值为 $\frac{R}{(1+i)^{n-1}}$

　　第n次支付租金的现值为 $\frac{R}{(1+i)^n}$

　　第一至第n次支付租金的现值和与租赁资产的概算成本相等，即：

　　 $P_v=\frac{R}{(1+i)} + \frac{R}{(1+i)^2} + ......+ \frac{R}{(1+i)^{n-1}} + \frac{R}{(1+i)^n}$ ...... ①

　　将上式进行简化，等式两边各乘以(1+i)，则：

　　 $P_v(1+i)=R + \frac{R}{(1+i)} + \frac{R}{(1+i)^2} + ......+ \frac{R}{(1+i)^{n-2}} + \frac{R}{(1+i)^{n-1}}$ ...... ②

　　以②-①，则

　　 $P_v(1+i)-P_v=R- \frac{R}{(1+i)^n}= \frac{(1+i)^n-1}{(1+i)^n} \times R$

　　 $P_v \times i=\frac{(1+i)^n-1}{(1+i)^n} \times R$

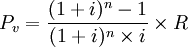
　　 $P_v=\frac{(1+i)^n-1}{(1+i)^n \times i} \times R$

　　 $R=P_v\cdot\frac{i(1+i)^n}{(1+i)^n-1}$

2．有宽限期的期末后付租金复利等额年金法计算公式。有宽限期的期末付租公式。其原理与期末付租基本相同，只是将宽限期的本利和作为实租的总成本。宽限期的本利和为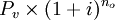： $P_v \times (1+i)^{n_o}$ 其中no为宽限期计息次数，所以，有宽限期的期末付租公式为：

　　 $R=P_v(1+i)^n_o \times \frac{(1+i)^n \times i}{(1+i)^n - 1}$

3，期初先付租金复利定额年金法计算公式。期初付租，第一次付租日即为成交日，那么，第一次付租额与其现值相等，所以：

　　第一次的现值为R

　　第二次的现值为 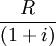$\frac{R}{(1+i)}$

　　......

　　最后一次的现值为 $\frac{R}{(1+n)^{n-1}}$

　　第一次至最后一次支付租金的现值即为租赁资产的概算成本，故：

　　 $P_v = R + \frac{R}{(1+i)} + \frac{R}{(1+2)^2} + ......+ \frac{R}{(1+i)^{n-1}}$ ……①

　　等式两边各乘以 $\frac{1}{(1+i)}$ ，则：

　　 $P_v \frac{1}{(1+i)}=\frac{R}{(1+i)}+\frac{R}{(1+i)^2}+......+\frac{R}{(1+i)^{n}}$ ...... ②

　　以①-②，则

　　 $P_v-P_v \frac{1}{(1+i)} = R - \frac{R}{(1+i)^n}$

　　 $P_v[1- \frac{1}{(1+i)}] = \frac{(1+i)^n-1}{(1+i)^n} \times R$

　　 $P_v[\frac{i}{(1+i)}] = \frac{(1+i)^n - 1}{(1+i)^n} \times R$

　　 $P_v= \frac{(1+i)[(1+i)^n-1]}{(1+i)^n \times i} \times R$

　　 $R=P_v \times \frac{(1+i)^{n-1} \times i}{(1+i)^n-1}$

等额年金法计算应用实例

　　某企业向某租赁机构租用一套设备，购价95000元，运输费、保险费，安装调试费5000元，租赁期限三年，年租赁费率10％，每季度付租一次，按期末后付、宽限期6个月期末后付和期初先付三种复利年金方法计算租金：

　　已知：P_v＝95000+5000=100000

　　n＝36÷3＝12

　　i=10％÷4＝0.1÷4＝0.025

　　1．用期末后付年金法计算：

　　每期租金 $R=P_v \times \frac{(1+i)^n \times i}{(1+i)^{n-1}}=100000 \times \frac{(1+0.025)^{12} \times 0.025}{(1+0.025)^{12} - 1}=9748.7l$ (元)

　　总租金 $\sum R=12 \times R = 12 \times 9748.71 = 116984.52$ (元)

　　2．用期初先付年金法计算：

　　每期租金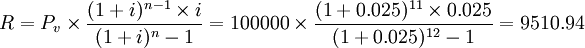 $R=P_v \times \frac{(1+i)^{n-1} \times i}{(1+i)^n -1} = 100000 \times \frac{(1+0.025)^{11} \times 0.025}{(1+0.025)^{12} - 1}=9510.94$ (元)

　　总租金 $\sum R = 12 \times R = 12 \times 9510.94 = 11431.28$ (元)

　　3．用宽限期6个月后付年金法计算：

　　每期租金

　　 $R = P_v \times (1+i)^{n_o} \times \frac{(1+i)^n \times i}{(1+i)^n - 1}=100000 \times (1+0.025)^2 \frac{(1+0.025)^{10} \times 0.025}{(1+0.025)^{10} - 1}=12004.32$ (元)

　　总租金 $\sum R = 10 \times R = 10 \times 12004.32=120043.20$ (元)

参考链接:https://wiki.mbalib.com/wiki/等额年金法

参考链接：https://wenku.baidu.com/view/4c338472aaea998fcd220e3a.html