题目描述:假设有一个硬币,抛出字(背面)和花(正面)的概率都是0.5,而且每次抛硬币与前次结果无关。现在做一个游戏,连续地抛这个硬币,直到连续出现两次字为止,问平均要抛多少次才能结束游戏?注意,一旦连续抛出两个“字”向上游戏就结束了,不用继续抛。
上面这个题目我第一次见到是在pongba的TopLanguage的一次讨论上,提出问题的人为Shuo Chen,当时我给出了一个解法,自认为已经相当简单了,先来考虑一下抛硬币的过程:首先先抛一枚硬币,如果是花,那么需要重头开始;如果是字,那么再抛一枚硬币,新抛的这枚如果也是字,则游戏结束,如果是花,那么又需要重头开始。根据这个过程,设抛硬币的期望次数为T,可以得到关系
T = 1 + 0.5T + 0.5( 1 + 0.5 * 0 + 0.5T)
解方程可得到 T = 6. 由于上面这个方法只能得到期望,而无法得到方差以及具体某个事件的概率,后来我又仔细分析了一下,推出了概率生成函数为(推导的过程暂时略过,后面你会看到一个更一般、更简单的推导)
于是可以算出方差 V = G''(1) + G'(1) - G'(1)^2 = 22。将G(z)根据Rational Expansion Theorem [CMath 7.3]展开,可以得到需要抛n次硬币的概率为
其中Fn是Fibonacci数列的第n项。到这里,我觉得这个问题似乎已经完全解决了,直到昨天看到Matrix67的牛B帖。在此帖中Matrix67大牛用他那神一般的数学直觉一下将需要连续抛出n个字的一般情形给解决了,而且得出的结果相当简洁:Tn = 2^(n+1) - 2,其中Tn为首次出现连续的n个字的期望投掷数。这也给了我一些启发,我试着将上面的过程进行推广,居然得到一个简单得出人意料的解法(甚至比上面n=2的推导过程还简单)。这个解法的关键在于下面这个递推关系
Tn = Tn-1 + 1 + 0.5 * Tn
也即是有 Tn = 2 * Tn-1 + 2。由于 T1 = 2,因此可以得到 Tn = 2^(n+1) – 2。上面的递推关系是怎么来的呢,一个直观的理解是这样的:首先先抛掷Tn-1次,得到连续的n-1个字,然后再抛一次,若是字,则游戏结束;否则需要重头开始,也就是说又需要 Tn 次。
期望投掷次数已经得出来了,但是我们还想知道方差、恰好需要投掷 m 次的概率等其它一些更具体的性质。为了方便理解概率的分布情况,我先用程序生成了一个概率表如下所示。在下表中,第n行、第m列的元素为 Pnm,表示首次出现连续n个字的投掷数为m的概率。
| 1/2 | 1/4 | 1/8 | 1/16 | 1/32 | 1/64 | 1/128 | 1/256 | 1/512 | 1/1024 |
| 0 | 1/4 | 1/8 | 2/16 | 3/32 | 5/64 | 8/128 | 13/256 | 21/512 | 34/1024 |
| 0 | 0 | 1/8 | 1/16 | 2/32 | 4/64 | 7/128 | 13/256 | 24/512 | 44/1024 |
| 0 | 0 | 0 | 1/16 | 1/32 | 2/64 | 4/128 | 8/256 | 15/512 | 29/1024 |
| 0 | 0 | 0 | 0 | 1/32 | 1/64 | 2/128 | 4/256 | 8/512 | 16/1024 |
仔细观察上表,你发现什么有趣的性质没?如果忽略掉分母的话,那么第n行恰好是一个n阶Fibonacci数列。例如可以考查各行的最后一列,有
第一行:1 = 1
第二行:34 = 21 + 13
第三行:44 = 24 + 13 + 7
第四行:29 = 15 + 8 + 4 + 2
第五行:16 = 8 + 4 + 2 + 1 + 1
怎么解释这个现象呢?我们再来仔细考虑一下掷硬币的过程,为方便在下文中用1表示字,用0表示花,于是我们的目标是要恰好使用m次投掷,得到连续的n个1.
若第一次的结果为 0,那么剩下的任务就是恰好使用m-1次投掷得到到连续的n个1.
若前两次的结果为 10, 那么剩下的任务就是恰好使用m-2次投掷得到到连续的n个1.
若前三次的结果为 110, 那么剩下的任务就是恰好使用m-3次投掷得到到连续的n个1.
若前四次的结果为 1110, 那么剩下的任务就是恰好使用m-4次投掷得到到连续的n个1.
…
若前n-1次的结果为 1…10(n-2个1), 那么剩下的任务就是恰好使用1次投掷得到到连续的n个1.
你或许已经看出来了,这里实际上是在枚举首次出现0的位置。由于首个0出现在位置i的概率为1/2^i,于是得到Pnm的递推公式
于是根据初始条件:,
,我们可以推出所有事件的概率。现在来推一下概率生成函数,设需要得到连续n个1的投掷数的概率生成函数为Gn(z),于是有
根据上面的递推公式和初始条件,可以得到
于是可解得
分别代入 n = 1 和 n = 2 可以得到
以我们前面得到的结果一致,这证明这个概率生成函数的确是正确的。有了生成函数后,我们又多了一种计算期望的方式
而方差也可以非常容易的得到
至此,这个抛硬币的问题终于应该算是被完全解决了,完。
转载地址 点击打开链接
一个骰子,6面,1个面是 1, 2个面是2, 3个面是3, 问平均掷多少次能使1,2,3都至少出现一次?
一共有三种方法可以解此问题:概率公式、分叉树递归列方程法、指示器变量法。
1. 方法一:概率公式
化为概率的表示是:
1发生 的概率是1/6, 2发生的概率是2/6, 3发生的概率是3/6,求1,2,3至少出现一次的投掷次数的期望。
思路:
第一二次肯定不可能出现这种情况
第x(x > 2)次三个都出现的情况分三种(x ^ y 表示 x 的 y 次方)
1:第x次出现 1,那么前面出现的必然是 2 和 3 ,且至少出现一次
出现1的概率为 1 / 6,前面x-1次不出现1的概率为(1 - 1 / 6) ^ (x - 1),但是其中包含全是 2 和全是 3 的情况,去掉全 2 的概率 (1 / 2) ^ (x - 1),全部为3的概率(1 / 3) ^ (x - 1),那么情况 1 的概率为 ((1 - 1 / 6) ^ (x - 1) - (1 / 2) ^ (x - 1) - (1 / 3) ^ (x - 1)) * (1 / 6)
2:第x次出现2,那么前面出现的必然是 1 和 3 ,且至少出现一次
同样,概率为 ((1 - 1 / 3) ^ (x - 1) - (1 / 2) ^ (x - 1) - (1 / 6) ^ (x - 1)) * (1 / 3)
3:第x次出现3,那么前面出现的必然是 1 和 2 ,且至少出现一次
同样,概率为 ((1 - 1 / 2) ^ (x - 1) - (1 / 3) ^ (x - 1) - (1 / 6) ^ (x - 1)) * (1 / 2)
p(x)就为上面三种情况的和
那么,根据期望公式,平均值就等于从x = 3 到 n(无穷)求(x * p(x))的和
利用错位相减法计算极限值

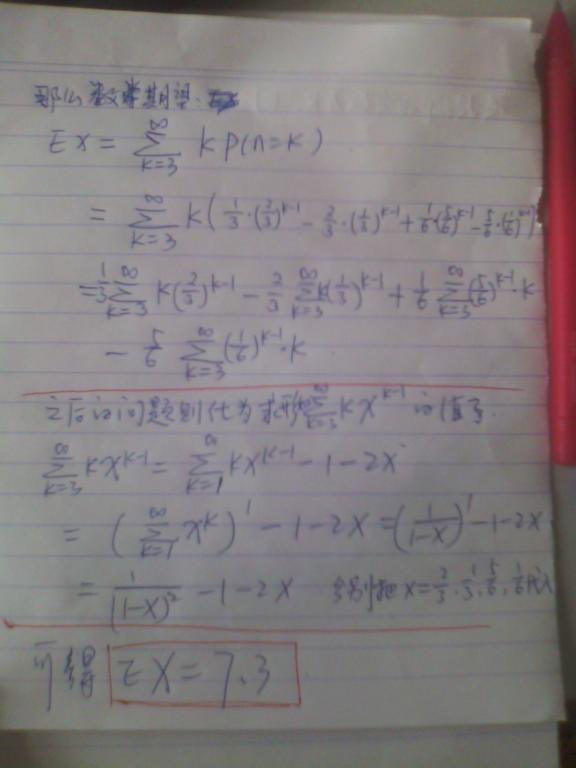
到此可以算出期望为7.3。






















 4532
4532

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








