Bring Old Photos Back To Life-----原理的整理总结

最新推荐文章于 2024-03-19 09:50:04 发布

sbh52113

最新推荐文章于 2024-03-19 09:50:04 发布

阅读量1.7k

点赞数 4

文章标签：计算机视觉人工智能

本文链接：https://blog.csdn.net/sbh52113/article/details/125458745

版权

本文介绍了针对老照片修复的深度学习方法，提出三重域转换模型，利用变分自编码器对合成与真实照片的潜在空间进行对齐。模型通过学习合成图像对之间的映射关系，应用到真实图像上实现修复。同时，引入非局部神经网络模块以捕获全局信息，增强修复效果。损失函数结合了KL散度、像素级损失和感知损失，确保生成图像的质量和真实性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

5.1 Non-local Neural Networks简介

5.1.1 核心思想

5.1.2 网络结构

5.2 本文非局部块的设计

1. 思考

在做整篇论文的整理之前，我先对一些对研读该论文有用的问题进行简要的回答（回答内容仅为个人理解及观点，仅供参考）
Q1:论文试图解决什么问题?
A1:现实生活中的老照片退化过程要比合成照片的退化复杂的多（我们不能完全模拟照片的整个退化过程），所以用合成照片去训练我们的模型，就会导致训练出来的模型的泛化能力比较差，因此我们就需要一个新的方法来解决这个问题。
Q2:这篇文章要验证一个什么科学假设？
A2:模型可以学习合成照片之间的转化关系，并将这种转换关系推广到真实照片中。
Q3:论文中提到的解决方案之关键是什么？
A3:提出一个三重域转换模型，使用生成模型将合成图像对以及真实图片下放到潜在域，并且使合成的旧图像的潜在域尽量逼近真实旧图像，最后学习合成图片对之间的映射关系并扩展到真实图像。

下面是对文章正式的介绍：

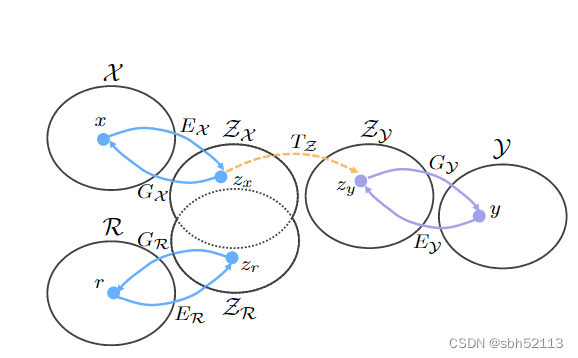
2. 算法简介

设 $x$ 为合成的破损老照片， $y$ 为合成的无破损老照片（ $x$ 是由 $y$ 通过人为损坏而得来的）， $r$ 为输入的真实的老照片。用 $\mathcal{R}$ 来表示真实老照片集合所在域， $\mathcal{X}$ 为合成的破损老照片集合所在域， $\mathcal{Y}$ 为Ground Truth所在的空间域。

作者使用了两个变分编码器 $(VAE_1,VAE_2)$ 。 $VAE_1$ 将 $x,r$ 投影到潜在空间域 ${\mathcal{Z}}_{\mathcal{X}},{\mathcal{Z}}_{\mathcal{R}}$ ，并使其尽量相等，而另一个变分编码器则是将y投影到潜在空间 ${\mathcal{Z}}_{\mathcal{Y}}$ 。

注：这里用的是变分自编码器，其目的是使照片在潜在空间满足高斯分布。

因为人工合成的照片和真实照片的损坏方式还是具有一定的联系的，故我们能通过变分自编码器将 ${\mathcal{Z}}_{\mathcal{X}},{\mathcal{Z}}_{\mathcal{Y}}$ 对齐。再通过学习 $x,y$ 之间的映射关系将 $x$ 从 $\mathcal{X}$ 域映射到 $\mathcal{Y}$ 域，进而输出被修复图片 $x$ 。又因为 ${\mathcal{Z}}_{\mathcal{X}},{\mathcal{Z}}_{\mathcal{R}}$ 两个域非常逼近，故我们可以让 $y$ 具有前面 $x$ 转换关系，从而修复真实的老照片。

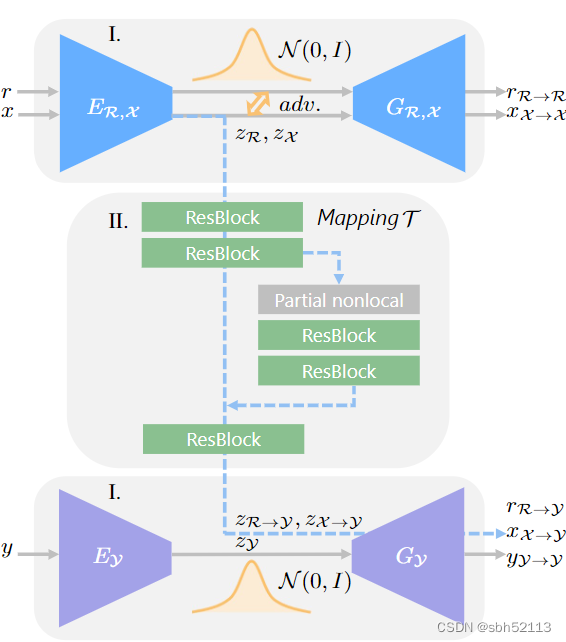
3. Loss的定义

这里先给出整个模型的框架图，一篇好的文章，看完画的框架图后对作者的思路就有了大致的了解。

3.1. $VAE_1$ 的损失函数

$VAE_1$ 的损失函数可以定义为（这里只给出有关r的损失，有关x的损失与其类似）：

KL散度是为了规定潜在空间满足高斯分布，第二项就是为了使Generation的Output ${r_{\mathcal{R}}}\rightarrow{\mathcal{R}}$ 更接近Input。又为了使输出的图像更加平滑，本文引入第三项 $\mathcal{L}_{VAE_1,GAN}(r)$ ，其原理与LSGAN的Loss定义一致。

对于两个变分编码器，作用都是为了对齐潜在空间，所以其损失的定义一样，故 $VAE_2$ 的损失函数推导过程同理可得。

补充：LSGAN是一种对训练loss的改进方法。它使用Least Squares作为loss，想让梯度能更有效的传递回去。

3.2 LSGAN

可以看到式（1）为传统的GAN的损失函数，式（2）为改进后的LSGAN的损失，由于没有log存在，所以反向传播会更加容易。

到这里还有一个问题没有解决，那就是具体怎么控制 ${\mathcal{Z}}_{\mathcal{X}},{\mathcal{Z}}_{\mathcal{R}}$ 使其十分接近呢？基于此问题，本文引出了另一个损失函数的定义：

这个思路和LSGAN的loss思路基本是一样的，r可以认为是GAN中的生成器输入端的噪声。

上面的这些loss定义都理解了之后，下来就可以给出整个生成模型 $VAE_1$ 的总的loss的定义为：

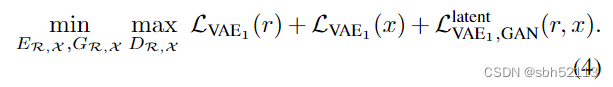
4. 图像修复

由上图可知，两个经过对齐的潜在空间 ${\mathcal{Z}}_{\mathcal{X}},{\mathcal{Z}}_{\mathcal{R}}$ 通过 $Mapping \mathcal{T}$ 模块去学习到 ${\mathcal{Z}}_{\mathcal{Y}}$ 的映射，前面已经讲过， $\mathcal{Z}_\mathcal{X}\rightarrow\mathcal{Z}_\mathcal{Y}$ 比较容易，因此模型可以容易的学到此映射关系，又因为 ${\mathcal{Z}}_{\mathcal{X}},{\mathcal{Z}}_{\mathcal{R}}$ 经过对齐已经非常接近，所以 $\mathcal{Z}_\mathcal{R}\rightarrow\mathcal{Z}_\mathcal{Y}$ 的映射关系模型也会学到。

在训练过程中我们先训练 $\small VAE$ 模型，并将训练好的 $\small VAE$ 模型的参数固定，进而去学习训练 $\small Mapping \mathcal{L}$ 模块。

设 $\small x,y,r$ 最终的输出分别为 $\small x_\mathcal{X}\rightarrow\mathcal{Y},y_\mathcal{Y}\rightarrow\mathcal{Y},r_\mathcal{R}\rightarrow\mathcal{Y}$ ,注意这里的 $\small \mathcal{Y}$ 指的的是x,y,r的最终输出属于前面所提到的 $\small \mathcal{Y}$ 空间域，即Ground Truth所在的空间域，是泛指，并不是指一个固定的输出 $\small \mathcal{Y}$ 。

$\small Mapping \mathcal{L}$ 模块损失函数的定义为：

其中第一项 $\small \mathcal{L}_{\mathcal{T}},_{\ell_1}$ wei是为了使 $\small {\mathcal{Z}}_{\mathcal{X}}$ 映射到 ${\mathcal{Z}}_{\mathcal{Y}}$ ，表达式为：

第二项依旧以LSGAN的损失为基础，来使x最终的输出更好，确保网络可以对x进行正确的修复。

对于第三项，引入了感知损失函数(Perceptual Loss )，其目的是为了稳定GAN的训练，众所周知GAN这个模型很魔性，不过其训练困难以及不稳定也是其最难处理的因素之一。

第三项 $\small \mathcal{L}_F_M$ 的表达式如下：

其中 $\small \phi^{i}_{D\mathcal{T}}(\phi^{i}_{VGG})$ 为判别器的第i层特征图， $\small n^{i}_{D\mathcal{T}}(n^{i}_{VGG})$ 为第i层的激活次数，也就是激活函数的个数。

5. 多重退化重建

由于我们使用的残差网络每一层的感受野是有限的，所以网络可能更注重于局部特征，导致网络对全局特征的把握比较匮乏，对于图片中结构化缺失的部分来说，往往需要依靠全局信息特征来进行修复。而非结构化缺失则更需要依靠局部特征去修复，由于真实的老照片往往同时具备这两种缺陷，因此我们的网络必须同时具备这两种能力。

非局部模块非常好构建，直接用Resnet就可搭建，对于非局部模块本文采用Non-local Neural Networks的思想。

5.1 Non-local Neural Networks简介

5.1.1 核心思想

非局部操作算子是基于非局部均值操作而提出的，故首先来介绍下非局部均值操作。

在传统CNN或者传统的图像卷积算法当中卷积过程如下：

可以看出来特征图中的每个像素都是有原图像的局部和kernel卷积而来的，而非局部均值操作在计算每个像素位置输出的时候不再只和邻域计算；而是和图中所有位置的像素都计算其相关性。然后根据相关性大小来对原图中的每个位置像素都赋予权重（相关性大的权重高，反之），然后将所有加权的像素进行求和得出输出特征图当前位置的像素值。具体过程如下所示：

可以看出对于待计算的中心红色点，前两种都是在局部进行操作，而对于第三幅图则是和整幅图片进行计算。但实际上如果采用逐点计算方式（也就是以像素点为单位），不仅计算速度慢，而且抗干扰能力不太友好，故采用Block的思想，计算Block于Block之间的相关性。

可以看出，待计算的像素位置是p，故先构造block，然后计算其他位置block和当前block的相关性，可以看出q1和q2区域和q非常相似，故计算时候给予一个大权重，而q3给予一个小的权重。这样的做法可以突出共性(关心的区域)，消除差异(通常是噪声)。

上面的所有分析都是基于非局部操作来讲的，但是实际上在深度学习时代，可以归为自注意力机制Self-attention。在CV中那就是通过关注图片中(可以是特征图)所有位置并在嵌入空间中取其加权平均值来表示图片中某位置处的响应。嵌入空间可以认为是一个更抽象的图片空间表达，目的是汇聚更多的信息，提高计算效率。听起来非常高级的样子，到后面可以看出，是非常简单的。

5.1.2 网络结构

在深度学习中非局部操纵可以表达为：

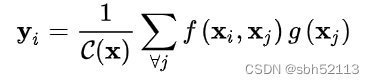
i是输出特征图的其中一个位置，通用来说这个位置可以是时间、空间和时空。j是所有可能位置的索引， $x$ 是输入信号，可以是图像、序列和视频，通常是特征图。 $y$ 是和 $x$ 尺度一样的输出图，f是配对计算函数，计算第i个位置和其他所有位置的相关性，g是一元输入函数，目的是进行信息变换， $\mathcal{C}(x)$ 是归一化函数，保证变换前后整体信息不变。以上是一个非常泛化的公式，具体细节见下面。在局部卷积算子中，一般是 $i-1<=j<=i+1$ 。

由于f和g都是通式，故结合神经网络特定，需要考虑其具体形式。

首先g由于是一元输出，比较简单，我可以采用 $1\times 1$ 卷积，代表线性嵌入，其形式为：

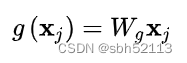
对于f，前面我们说过其实就是计算两个位置的相关性，那么第一个非常自然的函数是Gaussian。

(1) Gaussian

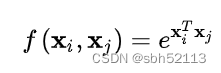
对两个不同位置先进行点乘，然后通过指数映射放大差异。

(2) Embedded Gaussian

前面的Gaussian形式是直接在当前空间计算，而(2)更加通用，在嵌入空间中计算高斯距离。这里：

$\mathcal{C}(x)$ 的表达式为：

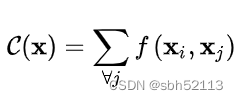
仔细看，如果我们把 $\mathcal{C}(x)$ 考虑上那么整个非局部化式子的表达式就可以表示为SoftMax的形式，即：

这个就是目前常用的位置注意力机制的表达式，语义分割大部分通道注意力机制都是本文的特殊化。

(3) Dot Product

其中 $\mathcal{C}(x)=N$ ,N为像素个数。可以看出（2）（3）的主要区别是是否含有激活函数SoftMax。

(4) Concatenation

参考Relation Networks可以提出：

前面是基本的非局部操作算子，利用这些算子，下面开始构造成模块。

可以看出，上面构造成了残差形式。上面的做法的好处是可以随意嵌入到任何一个预训练好的网络中，因为只要设置W_z初始化为0，那么就没有任何影响，然后在迁移学习中学习新的权重。这样就不会因为引入了新的模块而导致预训练权重无法使用

5.2 本文非局部块的设计

本文非局部块的思路和上面大致是一样的，都用到了Gaussian函数。很多人看了这篇论文对这部分都似懂非懂不知道在说什么，我这里先给出公式：

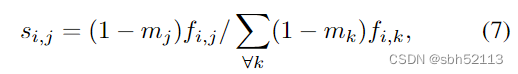
其中

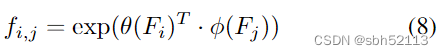
仔细对比发现这个公式其实就是上面非局部操作中公式的变种，不一样的一点就是多了一项 $(1-m_k)$ 。我们令 F为 $\small Mapping \mathcal{L}$ 模块的特征图 $m\in {\left \{ 0,1 \right \}}^{HW}$ 。当m=1时表示此位置为掩码区域，m=1时为正常区域。这样做的目的其实就是为了在相关性计算的时候只计算非掩码区域的相关性。这里的 ${\phi},{\theta}$ 与非局部网络中Embedded Gaussian意思是一样的。