史无前例的做出C题啊!!!激动ing~~。。。
#include <stdio.h>
int main()
{
int n, a[101], i, j, x, s, b[101]= {0}, z = 0, y = 0;
scanf("%d",&n);
s=n;
for(i=0; i<n; i++)
{
scanf("%d",&a[i]);
b[a[i]]++;
if(y<a[i])
y=a[i];
}
while(s)
{
x=0;
for(i=0; i<=y; i++)
{
while(b[i]&&i>=x)
{
x++;
b[i]--;
s--;
}
}
z++;
}
printf("%d\n",z);
return 0;
}







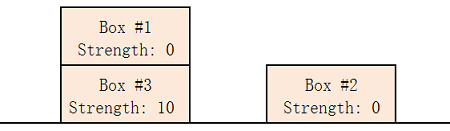
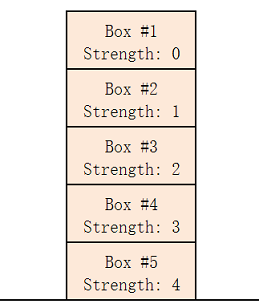














 935
935

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








