一 快速幂
目的:当我们在求f(x) = a ^ x % mod时,f(x)的结果会呈指数型增加,如果我们在最终求完之后进行取模,那么最终的那个结果无论int 或者 long long 都无法装下这么大的数据。
所以我们需要一个防爆的方法来求出正确答案
那么有人问了:如果我要是求把x次方拆分成x个a相乘,每次进行取模可以吗?这样做有问题吗?没有问题,它可以出答案,但时间复杂度太高,太慢了我们能接受吗?不能接受,我们不但要出答案,还要更快
那么我们就需要引入快速幂这个方法了
我们先来看下取模运算的规则:
(a + b) % mod = (a % mod + b % mod) % mod
(a - b) % mod = (a % mod - b % mod) % mod
(a * b) % mod = (a % mod * b % mod) % mod
其实最重要的就是知道第三条规则就可以
比如让你求9 ^ 14
9 ^ 15 % mod = (9 * 9) * (9 * 9 * 9 * 9) * (9 * 9 * 9 * 9 * 9 * 9 * 9 * 9) % mod
= 9 ^ (2 + 4 + 8)% mod
= ((9 ^ 2) * (9 ^ 4) * (9 ^ 8)) % mod
= ((9 ^ 2 % mod) % mod* (9 ^ 4 % mod) % mod * (9 ^ 8 % mod) % mod) % mod
我们可以对指数进行二进制拆分
15 = 1110B
9 ^ 15 = 9 ^ (10B + 100B + 1000B)
那么我们只需要进行位运算,从第一位到最后一位判断在当前位是否是1
具体看代码吧
模板
ll quick(ll a, ll b, ll mod) {
ll ans = 1;
while (b) {
if (b & 1) {
ans *= a;
ans %= mod;
}
a = a * a % mod;
b >>= 1;
}
return ans;
}
模板例题
二 快速乘
快速乘的思路是类似的
那么我们在什么时候,或者说,为什么要用快速乘呢?
我们已经学会了快速幂,那么我们在进行快速幂的时候,如果给出的mod很大的时候,那么就很有可能在每步拆分的时候就已经炸long long了,那么我们还要在每次相乘的时候防爆
思路和快速幂类似,这里就不做概述了
有问题吗?没有问题 nice
模板
ll mul(ll a, ll b, ll mod) {
ll ans = 0;
while (b) {
if (b & 1) {
ans += a;
ans %= mod;
}
a <<= 1;
a %= mod;
b >>= 1;
}
return ans % mod;
}
三 矩阵快速幂
先推荐一波b站大佬,不分解的AgOH,如果想看视频讲解可以看他的视频
b站链接
先来说一下矩阵相乘
他有这么一个公式
但懂得都懂,看公式多没意思
直接上图
如果还是不会,可以先去学习一下矩阵乘法
矩阵快速幂类似于快速幂,它同样也是根据指数的每一位是否是1进行操作,就是将原本快速幂的底数,换成了一个矩阵
要注意的一个地方就是矩阵的初始化,在快速幂中第一个ans一开始初始化成1,在矩阵快速幂中的初始化,是将要初始化的矩阵的主对角线全部初始化为1,其他全是0,这种矩阵叫做单位矩阵E。它与任意一个矩阵相乘都等于那个矩阵,与快速幂中的1 * a = a意思相同,只不过在这里是E * A = A
每个人代码模板不一样,我比较喜欢重载MAT的 * 直接对两个矩阵进行相乘。但是最后还是需要自己打出来一个模板,毕竟用自己的才是最舒服的呢。
例题
模板题
#include <cstdio>
#define ll long long
const ll MOD = 1000000007;
const int M = 100;
int n;
ll k;
struct MAT {
ll map1[M][M];
void init() {
for (int i = 1; i <= n; ++i) map1[i][i] = 1;
}
MAT() {
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
map1[i][j] = 0;
}
};
MAT operator* (MAT a, MAT b) {
MAT ans;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
for (int k = 1; k <= n; ++k) {
ans.map1[i][j] += a.map1[i][k] * b.map1[k][j] % MOD;
ans.map1[i][j] %= MOD;
}
}
}
return ans;
}
MAT POW_MAT(MAT a, ll k) {
MAT ans;
ans.init();
while (k) {
if (k & 1) {
ans = ans * a;
}
a = a * a;
k >>= 1;
}
return ans;
}
int main() {
scanf("%d%lld", &n, &k);
MAT ans;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
scanf("%d", &ans.map1[i][j]);
ans = POW_MAT(ans, k);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
printf("%d ", ans.map1[i][j]);
}
printf("\n");
}
return 0;
}
应用题1
#include <cstdio>
#include <iostream>
using namespace std;
#define ll long long
const int MOD = 10000;
struct MAT {
ll map1[3][3];
MAT() {
for (int i = 1; i <= 2; ++i)
for (int j = 1; j <= 2; ++j)
map1[i][j] = 0;
}
}new1;
MAT operator* (MAT a, MAT b) {
MAT ans;
for (int i = 1; i <= 2; ++i) {
for (int j = 1; j <= 2; ++j) {
for (int k = 1; k <= 2; ++k) {
ans.map1[i][j] += a.map1[i][k] * b.map1[k][j]; ans.map1[i][j] %= MOD;
}
}
}
return ans;
}
MAT POW_MAT(MAT a, int k) {
MAT ans;
for (int i = 1; i <= 2; ++i) ans.map1[i][i] = 1;
while (k) {
if (k & 1) {
ans = ans * a;
}
a = a * a;
k >>= 1;
}
return ans;
}
int main() {
int n;
MAT new1;
new1.map1[1][1] = 1;
new1.map1[1][2] = 1;
new1.map1[2][1] = 1;
while (scanf("%d", &n)) {
if (n == -1) break;
if (n == 0) { printf("0\n"); continue; }
printf("%lld\n", POW_MAT(new1, n).map1[1][2]);
}
return 0;
}
应用题2
本题不可以直接相加,看的上面的大佬的二分的方法
具体分为k奇偶两种情况
如果k是奇数 那么可以分成S(k) = A ^ (k / 2 + 1) * S(k / 2) + A ^ (k / 2 + 1) + S(k / 2)
如果k是偶数 那么可以分成S(k) = S(k / 2) + S(k / 2) * A ^ (k / 2)
具体可以看下下面的例子
k = 10 有: S(10) = ( A1+A2+A3+A4+ A^5 ) + A^5 * ( A1+A2+A3+A4+A^5 ) = S(5) + A^5 * S(5)
k = 5 有: S(5) = ( A1+A2 ) + A^3 + A^3 * ( A1+A2 ) = S(2) + A^3 + A^3 * S(2)
k = 2 有 : S(2) = A^1 + A^2 = S(1) + A^1 * S(1)。
最后进行二分递归就可以了
代码
#include <cstdio>
using namespace std;
const int M = 35;
int n, k, m;
struct MAT {
int map1[M][M];
MAT() {
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
map1[i][j] = 0;
}
};
MAT operator* (MAT a, MAT b) {
MAT ans;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
for (int k = 1; k <= n; ++k) {
ans.map1[i][j] += a.map1[i][k] * b.map1[k][j];
ans.map1[i][j] %= m;
}
return ans;
}
//
MAT operator+ (MAT a, MAT b) {
MAT ans;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
{
ans.map1[i][j] = a.map1[i][j] + b.map1[i][j];
ans.map1[i][j] %= m;
}
return ans;
}
MAT POW_MAT(MAT a, int k) {
MAT ans;
for (int i = 1; i <= n; ++i) ans.map1[i][i] = 1;
while (k) {
if (k & 1) {
ans = ans * a;
}
a = a * a;
k >>= 1;
}
return ans;
}
MAT ans(MAT a, int k) {
if (k == 1) return a;
MAT ans1, temp;
ans1 = ans(a, k / 2);
if (k & 1) {
temp = POW_MAT(a, k / 2 + 1);
return ans1 = temp * ans1 + temp + ans1;
}
else {
temp = POW_MAT(a, k / 2);
return ans1 = temp * ans1 + ans1;
}
}
int main() {
scanf("%d%d%d", &n, &k, &m);
MAT new1;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
scanf("%d", &new1.map1[i][j]);
new1 = ans(new1, k);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
printf("%d ", new1.map1[i][j]);
}
printf("\n");
}
return 0;
}








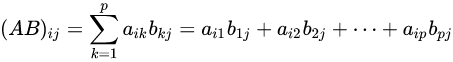
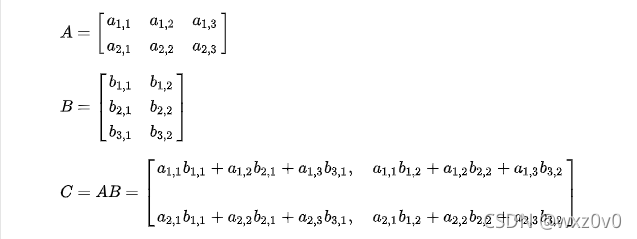













 611
611











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








