决策树是一个类似于流程图的树结构;其中,每个内部结点表示在一个属性上的测试,每个分枝代表一个测试输出,而每个树叶结点代表类或类分布。树的最顶层结点是根结点。一棵典型的判定树如下图。这是一个用于预测不同的天气条件下比赛是否能如期举行。
ID3算法
下面是著名的ID3算法的伪代码:
Generate_decision_tree(samples,attribute_list)
{
创建结点 N;
if samples 都在同一个类C then
return N 作为叶结点,以类C标记;
if attribut_list 为空 then
return N 作为叶结点,标记为samples中最普通的类;
选择attribute_list中具有最高信息增益的属性test_attribute
标记结点 N 为test_attribute
for each test_attribute 中的未知值ai :
{
由结点 N 长出一个条件为 test_attribute = ai的分枝;
设si 是samples 中test_attribute = ai的样本的集合;
if si 为空 then
加上一个树叶,标记为 samples中最普通的类;
else{
加上一个由 Generate_decision_tree(si, attribute_list–test_attribute)返回的 结点(子树);
}
}
}
可以看到,决策树生成算法一个重要的工作就是选择当前信息增益最大的属性对决策树进行分裂,并根据该属性可能的取值建立对应的分支。
这里的信息增益是涉及了信息论中信息熵的概念。信息熵是表示一个事件的不确定性的大小,不确定性越大那么该事件包含的信息熵就越大,如果一个事件完全确定了,那么它所包含的信息熵就是0。信息熵的计算公式如下,其中![]() 表示该事件最终结果为
表示该事件最终结果为![]() 的概率。
的概率。
信息增益就是分裂前的信息熵–分裂后的信息熵,信息增益越大就表示分裂过程中所释放的信息量就越大。
比如决策表的信息如下表:
| NO. | Outlook | Temperature | Windy | Humidity | Play? |
| 1 | sunny | hot | false | high | No |
| 2 | sunny | hot | true | high | No |
| 3 | overcast | hot | false | high | Yes |
| 4 | rain | mild | false | high | Yes |
| 5 | rain | cool | false | normal | Yes |
| 6 | rain | cool | true | normal | No |
| 7 | overcast | cool | true | normal | Yes |
| 8 | sunny | mild | false | high | No |
| 9 | sunny | cool | false | normal | Yes |
| 10 | rain | mild | false | normal | Yes |
| 11 | sunny | mild | true | normal | Yes |
| 12 | overcast | mild | true | high | Yes |
| 13 | overcast | hot | false | normal | Yes |
| 14 | rain | mild | true | high | No |
我们计算在决策树根节点处计算属性“Outlook”的信息增益。计算过程如下:
分裂前的信息熵= -p(noplay)log p(noplay)-p(play)log p(play)
= info([9,5]) = -(9/14)log(9/14)-(5/14)log(5/14)
=0.940 bits
= info([2,3]) + info([4,0]) + info([3,2])
=0.693 bits
“Outlook”的信息增益 gain(“Outlook”) = 0.940 - 0.693 = 0.247bits
用同样的方法可以计算得到在根节点处:
gain(“Temperature”) = 0.029 bits
gain(“Windy”) = 0.048bits
gain(“Humidity”) = 0.152 bits
可见在根节点处“Outlook”属性的信息增益最大,我们就选择“Outlook”作为根节点处的分裂属性。“Outlook”把决策树在根节点处分成了3个分支,每一个分支也都对应了一个子决策信息表,按照同样的方法建立子树。比如:“sunny”的那个分支对应的子决策表就是:
| NO. | Temperature | Windy | Humidity | Play? |
| 1 | hot | false | high | No |
| 2 | hot | true | high | No |
| 8 | mild | false | high | No |
| 9 | cool | false | normal | Yes |
| 11 | mild | true | normal | Yes |
这样依次递归建立决策子树,直到分裂属性为空或者学习样本为空或者所有的节点都属于同一类。
C4.5算法
本质上C4.5算法只能算是ID3算法的改进版本。C4.5对ID3的改进如下:
1、 改善ID3算法的归纳偏置问题
2、 可处理连续数值型属性的离散化问题
3、 对决策树采取后剪枝。
4、 可处理样本的属性值确实问题
归纳偏置问题
所有的学习器在学习的时候都是有偏见。ID3算法的偏见是信息熵理论胎里带的,它更偏向于属性值多的那些属性,这样的树分支多而且树比较短。这样可能带来的问题是样本被过早的分散到多个分支中,导致样本在下一级的训练中训练不足。
C4.5改善ID3的归纳偏置问题的方法是引入了信息增益率:
其中Gain就是ID3算法中的信息增益,SplitInfo是分裂信息,表示属性值的广度和均匀性。分类信息的定义如下:
还是以根节点处得“Outlook”属性为例进行说明,其分裂信息为:
SplitInfo(“Outlook”)= -(5/14)log(5/14)-(5/14)log(5/14)- (4/14)log(4/14)。
连续数值型属性的离散化
C4.5既可以处理离散型描述属性,也可以处理连续性描述属性。在选择某节点上的分枝属性时,对于离散型描述属性,C4.5的处理方法与ID3相同,对于连续数值型属性,处理方式如下:
1、 将该结点上的所有数据样本按照连续型描述属性的具体数值,由小到大进行排序,得到属性值的取值序列(A1,A2……An)。
2、 生成属性值的若干个划分点,每个划分点都可以把属性值集合分成两个域。一个比较简单的划分方法就是取n-1个划分点,划分点Vi=(Ai + Ai+1)/2
3、 分别计算按照每个划分点划分得到的信息增益或者增益率,把信息增益或者信息增益率最大的那个划分点最为连续数值型属性的离散化划分点。
采用了一种后剪枝方法
避免树的高度无节制的增长,避免过度拟合数据,该方法使用训练样本集本身来估计剪枝前后的误差,从而决定是否真正剪枝。方法中使用的公式如下:
其中N是实例的数量,f=E/N为观察到的误差率(其中E为N个实例中分类错误的个数),q为真实的误差率,c为置信度(C4.5算法的一个输入参数,默认值为0.25),z为对应于置信度c的标准差,其值可根据c的设定值通过查正态分布表得到。通过该公式即可计算出真实误差率q的一个置信度上限,用此上限为该节点误差率e做一个悲观的估计:
通过判断剪枝前后e的大小,从而决定是否需要剪枝。
对于缺失值的处理
在某些情况下,可供使用的数据可能缺少某些属性的值。假如〈x,c(x)〉是样本集S中的一个训练实例,但是其属性A的值A(x)未知。处理缺少属性值的一种策略是赋给它结点n所对应的训练实例中该属性的最常见值;另外一种更复杂的策略是为A的每个可能值赋予一个概率。例如,给定一个布尔属性A,如果结点n包含6个已知A=1和4个A=0的实例,那么A(x)=1的概率是0.6,而A(x)=0的概率是0.4。于是,实例x的60%被分配到A=1的分支,40%被分配到另一个分支。这些片断样例(fractional examples)的目的是计算信息增益,另外,如果有第二个缺少值的属性必须被测试,这些样例可以在后继的树分支中被进一步细分。C4.5就是使用这种方法处理缺少的属性值。








![clip_image001[15] clip_image001[15]](http://hi.csdn.net/attachment/201106/8/0_1307492623kvZW.gif)
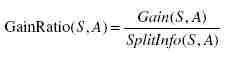
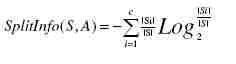



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








