Lesson 2 Gradient Desent

The goal is to find $X$ such that $\underset{X}{min}f(X)$

Using gradient descent algorithm to obtain the minimum value of the funtion.
let $y = f(x)$
Init: $x = x_0, y_0=f(x_0)$, iterative step $\alpha$, convergent precision $\epsilon$

The ith iterative formula can be expressed as:
$x_i = x_{i-1}-\alpha \nabla f(x_{i-1})$

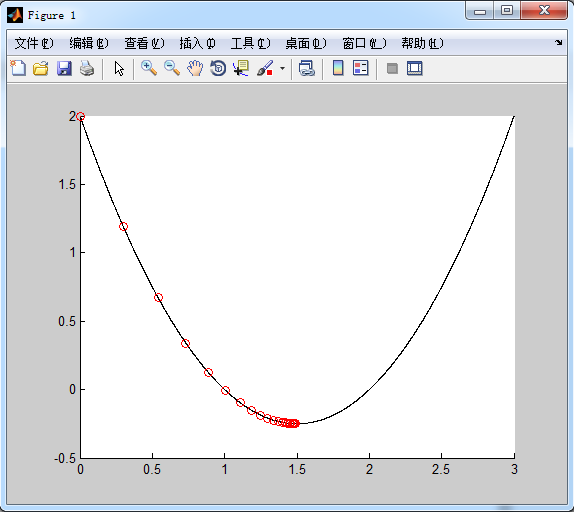
Example: solve the minimum of function $f(x) = x^2 + 3x + 2$

let $x_0 = 0$, step \alpha = 0.1, convergent precision $\epsilon = 10^{-4}$

f = @(x) x.^2 - 3*x + 2;
hold on
for x=0:0.001:3
    plot(x, f(x),'k-');
end

x = 0;
y0 = f(x);
plot(x, y0, 'ro-');
alpha = 0.1;
epsilon = 10^(-4);

gnorm = inf;

while (gnorm > epsilon)
    x = x - alpha*(2*x-3);
    y = f(x);
    gnorm = abs(y-y0);
    plot(x, y, 'ro');
    y0 = y;
end

let’s move into multi-variable case, say we have m samples, each sample has n features. $X$ is expressed as:

$$X = \begin{bmatrix} x_1^T\\ x_2^T\\ \vdots \\ x_m^T \end{bmatrix}$$
where

$$x_i = \begin{bmatrix} x_{i1}\\ x_{i2}\\ \vdots \\ x_{in} \end{bmatrix}$$
Then $X$ can be denoted as :
$$X = \begin{bmatrix} x_{11}&x_{11}&\cdots&x_{1n}\\ x_{21}&x_{21}&\cdots&x_{2n}\\ \vdots&\vdots&\ddots&\vdots \\ x_{m1}&x_{m1}&\cdots&x_{mn} \end{bmatrix}$$

Assuming $\displaystyle h(x_.)=\sum_{j = 1}^na_jx_{.j}=x_.^Ta$
Here,

$$a = \begin{bmatrix} a_{1}\\ a_{2}\\ \vdots \\ a_{n} \end{bmatrix}$$ is a unknown vector we need to solve.

$$Xa - y = \begin{bmatrix} h(x_1)-y_1\\ h(x_2)-y_2\\ \vdots \\ h(x_m)-y_m \end{bmatrix}$$

Now the objective function is $\underset{a}{min}f(a)=\frac{1}{2}(Xa-y)^T(Xa-y)$

Before the derivation, I would like to introduce some facts:
$tr(AB) = tr(BA)$ ………………………………..(1)
$tr(ABC)=tr(BCA)=tr(CAB)$………………………………..(2)
$tr(A)=tr(A^T)$ ………………………………..(3)
if $a\in R$, $tr(a) = a$………………………………..(4)
$\nabla_A tr(AB)=B^T$………………………………..(5)
$\nabla_Atr(ABA^TC)=CAB+C^TAB^T$………………………………..(6)

In order to obtain the critical points of $f(a)$, we take the derivative of $f(a)$ w.r.t $a$ and set it to be zero.

$$\begin{align} \nabla_a f(a)&=0\\ \nabla_a f(a)&= \nabla_a \frac{1}{2}(Xa-y)^T(Xa-y)\\ &=\frac{1}{2}\nabla_a (a^TX^TXa-a^TX^Ty-y^TXa+y^Ty)\\ &=\frac{1}{2}\nabla_a tr(a^TX^TXa-a^TX^Ty-y^TXa+y^Ty)\text{// the trace of a scalar is still a scalar}\\ &=\frac{1}{2}(\nabla_a tr(a^TX^TXa)-\nabla_a tr(a^TX^Ty) -\nabla_a tr(y^TXa)+\nabla_a tr(y^Ty))\\ &=\frac{1}{2}(\nabla_a tr(a^TX^TXa)-\nabla_a tr(y^TXa)-\nabla_a tr(y^TXa)+\nabla_a tr(y^Ty))\\ &=\frac{1}{2}(\nabla_a tr(a^TX^TXa)-2X^Ty)\\ &= \frac{1}{2}(\nabla_a tr(aa^TX^TX)-2X^Ty)\\ &= \frac{1}{2}(\nabla_a tr(aIa^TX^TX)-2X^Ty)\\ &= X^TXa-X^Ty=0 \end{align}$$

we can easily get a as follows:
$a=(X^TX)^{-1}X^Ty$

function [xopt,fopt,niter,gnorm,dx] = grad_descent(varargin)
% grad_descent.m demonstrates how the gradient descent method can be used
% to solve a simple unconstrained optimization problem. Taking large step
% sizes can lead to algorithm instability. The variable alpha below
% specifies the fixed step size. Increasing alpha above 0.32 results in
% instability of the algorithm. An alternative approach would involve a
% variable step size determined through line search.
%
% This example was used originally for an optimization demonstration in ME
% 149, Engineering System Design Optimization, a graduate course taught at
% Tufts University in the Mechanical Engineering Department. A
% corresponding video is available at:
% 
% http://www.youtube.com/watch?v=cY1YGQQbrpQ
%
% Author: James T. Allison, Assistant Professor, University of Illinois at
% Urbana-Champaign
% Date: 3/4/12

if nargin==0
    % define starting point
    x0 = [3 3]';
elseif nargin==1
    % if a single input argument is provided, it is a user-defined starting
    % point.
    x0 = varargin{1};
else
    error('Incorrect number of input arguments.')
end

% termination tolerance
tol = 1e-6;

% maximum number of allowed iterations
maxiter = 1000;

% minimum allowed perturbation
dxmin = 1e-6;

% step size ( 0.33 causes instability, 0.2 quite accurate)
alpha = 0.1;

% initialize gradient norm, optimization vector, iteration counter, perturbation
gnorm = inf; x = x0; niter = 0; dx = inf;

% define the objective function:
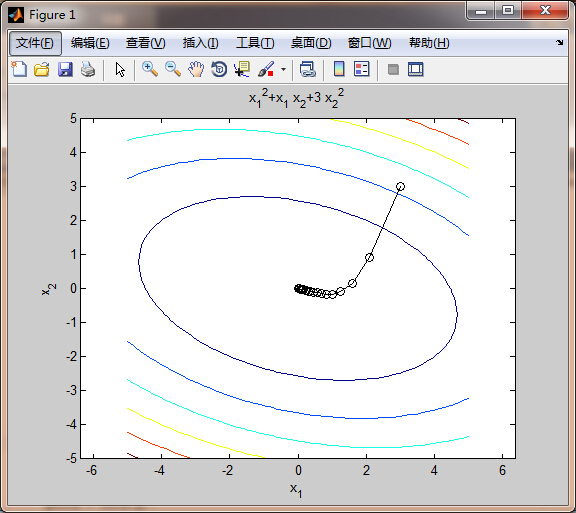
f = @(x1,x2) x1.^2 + x1.*x2 + 3*x2.^2;

% plot objective function contours for visualization:
figure(1); clf; ezcontour(f,[-5 5 -5 5]); axis equal; hold on

% redefine objective function syntax for use with optimization:
f2 = @(x) f(x(1),x(2));

% gradient descent algorithm:
while and(gnorm>=tol, and(niter <= maxiter, dx >= dxmin))
    % calculate gradient:
    g = grad(x);
    gnorm = norm(g);
    % take step:
    xnew = x - alpha*g;
    % check step
    if ~isfinite(xnew)
        display(['Number of iterations: ' num2str(niter)])
        error('x is inf or NaN')
    end
    % plot current point
    plot([x(1) xnew(1)],[x(2) xnew(2)],'ko-')
    refresh
    % update termination metrics
    niter = niter + 1;
    dx = norm(xnew-x);
    x = xnew;

end
xopt = x;
fopt = f2(xopt);
niter = niter - 1;

% define the gradient of the objective
function g = grad(x)
g = [2*x(1) + x(2)
    x(1) + 6*x(2)];

function [xopt,fopt,niter,gnorm,dx] = grad_descent(varargin)


if nargin==0
    % define starting point
    x0 = [3 3]';
elseif nargin==1
    % if a single input argument is provided, it is a user-defined starting
    % point.
    x0 = varargin{1};
else
    error('Incorrect number of input arguments.')
end

% termination tolerance
tol = 1e-6;

% maximum number of allowed iterations
maxiter = 1000;

% minimum allowed perturbation
dxmin = 1e-6;

% step size ( 0.33 causes instability, 0.2 quite accurate)
alpha = 0.1;

% initialize gradient norm, optimization vector, iteration counter, perturbation
gnorm = inf; x = x0; niter = 0; dx = inf;

% define the objective function:
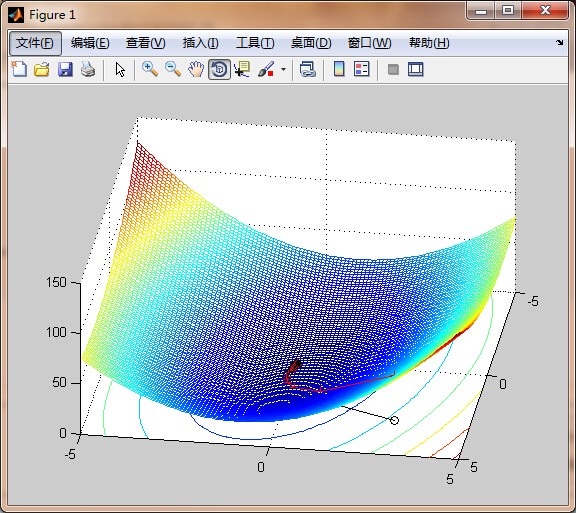
f = @(x1,x2) x1.^2 + x1.*x2 + 3*x2.^2;

m = -5:0.1:5;
[X,Y] = meshgrid(m);
Z = f(X,Y);

% plot objective function contours for visualization:
figure(1); clf; meshc(X,Y,Z); hold on

% redefine objective function syntax for use with optimization:
f2 = @(x) f(x(1),x(2));

% gradient descent algorithm:
while and(gnorm>=tol, and(niter <= maxiter, dx >= dxmin))
    % calculate gradient:
    g = grad(x);
    gnorm = norm(g);
    % take step:
    xnew = x - alpha*g;
    % check step
    if ~isfinite(xnew)
        display(['Number of iterations: ' num2str(niter)])
        error('x is inf or NaN')
    end
    % plot current point
    plot([x(1) xnew(1)],[x(2) xnew(2)],'ko-')
    plot3([x(1) xnew(1)],[x(2) xnew(2)], [f(x(1),x(2)) f(xnew(1),xnew(2))]...
        ,'r+-');
    refresh
    % update termination metrics
    niter = niter + 1;
    dx = norm(xnew-x);
    x = xnew;

end
xopt = x;
fopt = f2(xopt);
niter = niter - 1;

% define the gradient of the objective
function g = grad(x)
g = [2*x(1) + x(2)
    x(1) + 6*x(2)];