Function Maps: A Flexible Representation of Maps Between Shapes

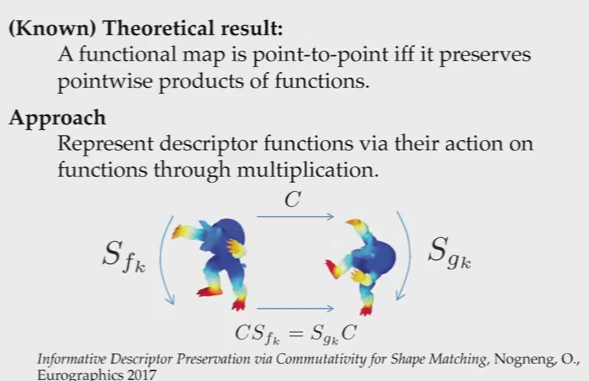
1) 图1， 先通过discriptor算出每点的值， 然后算出function map，即matrix $C$. 左图是说明discriptor每有区分左右， 中图加了对应约束使其左右交换， 右图为了说明function map满足代数运算， 左图减去中图就得到保方向的function map

2) section 4

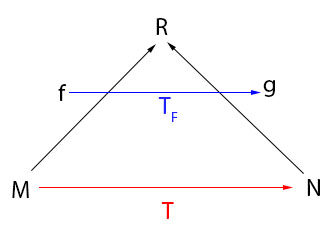
注意 $f,g$是从manifold上面到实数的函数， $T, T^{-1}$是从一个manifold到另一个manifold人映射，$T_F, T_F^{-1}$是从一个函数到另一个函数的映射。

$T_F(f) = g = f\circ T^{-1}$

3) Note that $C$ has a particularly … $c_{ij}=<T_F(\phi^M_i), \phi^N_j>$
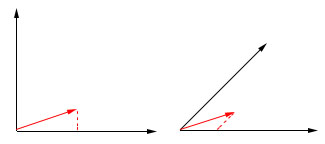
只有正交的时候内积才是投影

4） 图2主要说明near-isometric maps 的funtion map是一个稀疏，大体对角的矩阵。

5) 5.1 Indeed, … applications.
基为每点单色， 但是基的数量会很多， 并不compact. 然后图3阐述了不同数量的eigenvector作为基，最后得到的平均geodesic error.

关键句： maps that correspond to bigger deformations require more basis vectors, capturing the intuition that near-isometric maps are more compactly represented.

Note that the eigenfunctions of the unweighted discretization of Laplace-Beltrami operator provide a more compact representation of the map for the same quality of reconstruction.

6) 图4主要说明near-isometric maps induce matrices that are nearly sparse
the functional matrix $C$ stops being diagonal very quickly under even mild non-isometric deformations.

7) 图5主要说明functional representation的连续性， 这里通过插值的方式表现出来

8) 5.3讲各种constraints

9) Theorem5.1 看后面附录的证明，
$C_{i,j} = <T_F(\phi^M_i),\phi^N_j>=\int _N \phi^M_i\circ T^{-1}(y)\phi^N(y)\mu ^N(y)$
$D_{j,i} = <S_F(\phi^N_j),\phi^M_i>=\int _M \phi^N_j\circ T(x)\phi^M(x)\mu ^M(x)$

里面积分式一样， 外面体积一样， 所以$C = D^T$

10) 6.1 事件复杂度,建树$O(V_NlogV_N)$， 查找$O(V_MlogV_N)$

这里我想说说如何从函数的映射关系推导出点对点的映射关系，

注意看
$\delta$函数在基下面的映射
$\delta_x = lim_{t\rightarrow \infty}e^{-t\lambda_i \phi^M_i(x)\phi^N_i(\cdot)}$,
推导见【A Concise and Provably Informative Multi-Scale Signature
Based on Heat Diffusion】

当$t\rightarrow0$时， $e^{-t\lambda_i }$趋于1， 所以在点x处的$\delta$函数在Laplacian-Beltrami基下面（$B_M \times V_M$，$B_M$为LB基的数量）的系数为$\phi_i^M(x)$,即矩阵$\phi$第x列，该系数向量共有$B_M$个。

然后矩阵$C$是将$B_M$维的系数转到$B_N$维上的系数， (假设的$C$维数是$B_M \times B_N$, 根据需要自己转置， 反正就是从一个基的维度转到另一个基的维度)，然后这里的系数刚好又是$\phi_M$.

后面那个公式说明函数的差值跟系数差值成正比， 所以为了找出M上一点x对应于N上的某一点， 只需要找出$\delta_x$ 的系数，然后通过矩阵$C$，转到N下面的系数， 再于N下面$\delta$函数的系数作比较， 找出系数差距最小， 即找到了函数值差距最小。

整个过程是，对于M上的某一点x, 其$\delta_x$函数即在M的LB基下面的系数为$\phi^M(x)$, 转到N的LB基下的系数为$C\phi_i^M(x)$，该向量为$B_N \times 1$维,然后与N的LB基的每一列$\phi^N(y)$算距离（$\phi^N$的维数为$B_N \times V_N$），距离出最小的第y列，即为x的对应点。

11) 图6 说明他的方法比别人牛逼，竖轴为匹配部分的百分比

12) 图7 说明maps跟mesh的拓扑结构无关， 这里只用了x,y,z的坐标信息然后分别渲染到R,G,B通道

13) 图8说明他们的方法能帮别人提升（通过6.2）, 图9也是

14) 8.2是说一堆shape（shape collection）的匹配问题, 图10 a是原始错误， b是运行ICSM后的错误， c用diffusion运行在ICSM结果上。图11也是
15)说明segmentation的方法, 对于原模型的segmentation,每个区域用一个indicator function,然后转移到新的模型上

第一项是求funtional map $C$, 第二项是保isometric, 第三项是operator commutativity

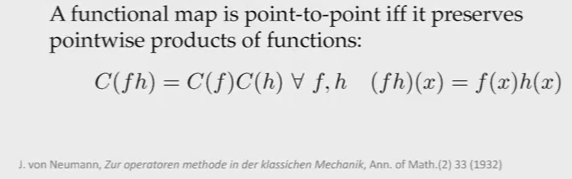
注意这里$S_{f_k}$和$S_{g_k}$是从一个函数变到另一个函数, 并且这两个函数都是作用于同一个manifold