1. 神经元模型
“M-P神经元模型”
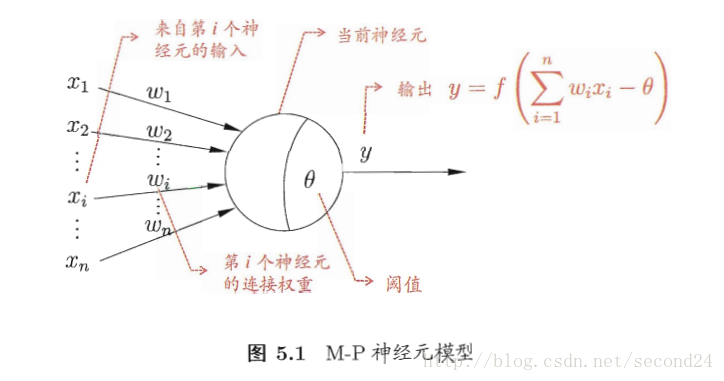
在这个模型中,神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值与神经元的阈值进行比较,然后通过“激活函数”处理以产生神经元的输出。
原理图如下:
激活函数
主要分为两种形式
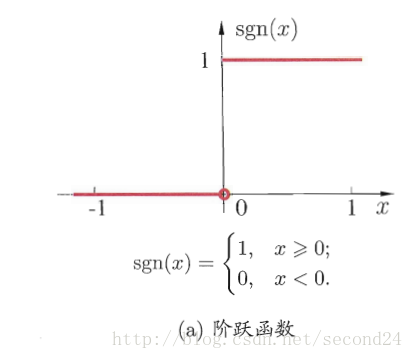
1. 阶跃函数
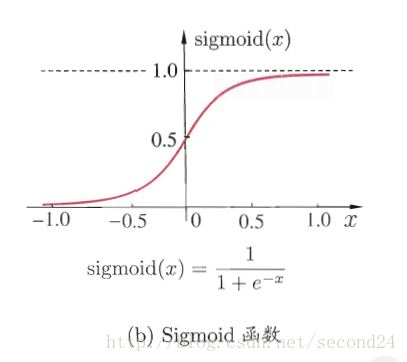
- Sigmoid函数
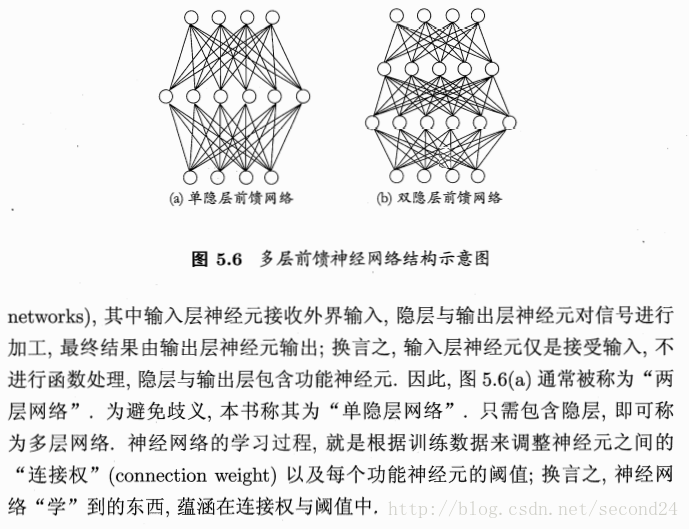
2. 感知机与多层网络
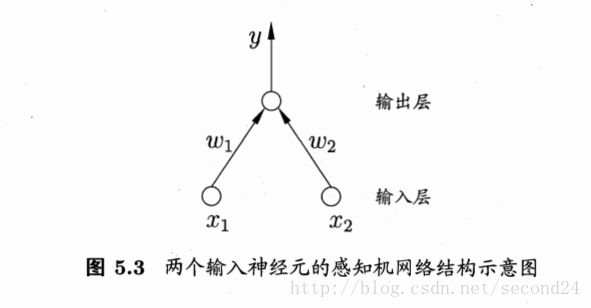
感知机由两层神经元组成,如图5.3所示,输入层接收外界输入信号后传递给输出层,输出层是M-P神经元(阈值逻辑单元)
感知机能容易地实现逻辑与、或、非运算。注意到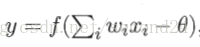
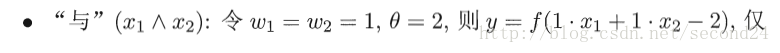
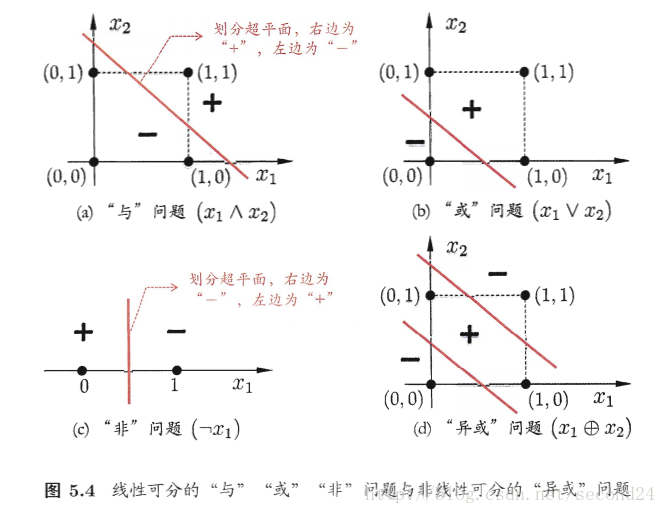
需要注意的是,感知机只有输出层神经元进行激活函数处理,即只拥有一层功能神经元,其学习能力非常有限。事实上,上述与、或、非问题都是线性可分的问题。
收敛:若两类模式是线性可分的,即存在一个线性超平面能将它们分开,则感知机的学习过程一定会收敛而求得适当的权向量;否则感知机学习过程将会发生震荡,权向量难以稳定下来,不能求得合适解。
隐层
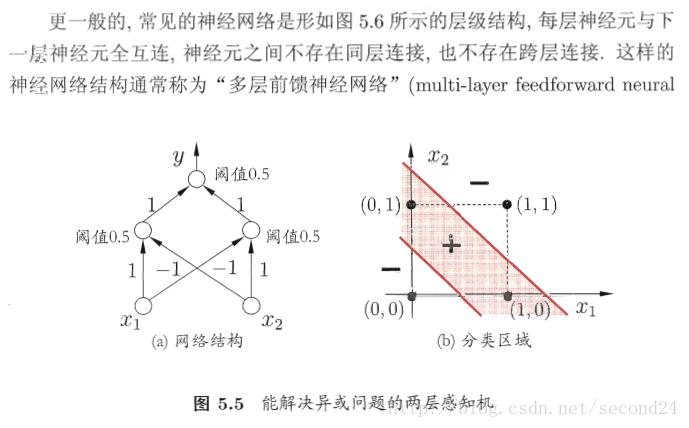
解决非线性可分问题,需考虑使用多层功能神经元。例如简单的两层感知机就能解决异或问题。输出层与输入层之间的一层神经元,被称为隐层或隐含层,隐含层和输出层神经元都是拥有激活函数的功能神经元。
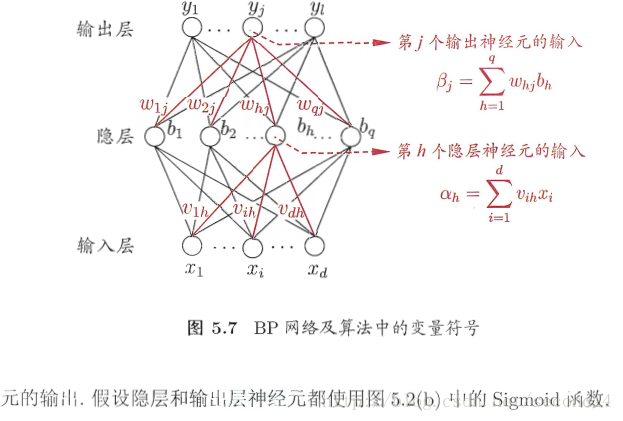
3. 误差逆传播算法
这种算法(简称BP)是为了训练多层网络,BP算法不仅可用于多层前馈神经网络,还可用于其他类型的神经网络,例如训练递归神经网络。
BP神经网络的具体应用及MATLAB代码
下面这个实验是BP神经网络用在数据预测上的小案例。
问题
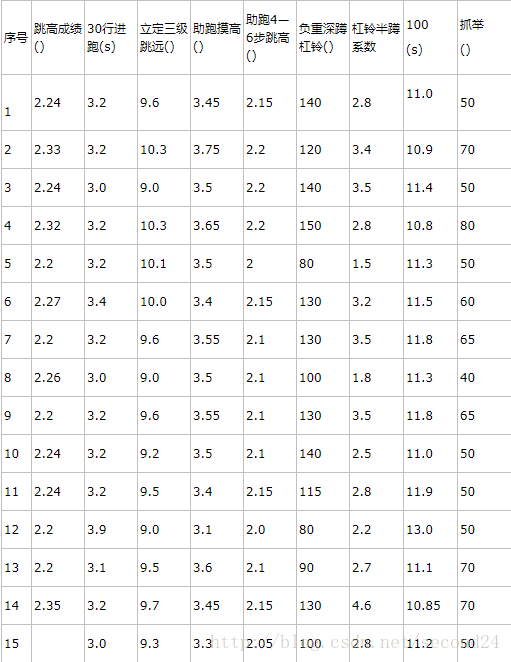
根据下表,预测序号15的跳高成绩
因为我们预测的是跳高成绩,因此需要把跳高成绩作为输出,其它各项指标作为输入。处理数据的时候需要用到premnmx函数将其归一化。(注意:每一列是一组输入训练集,行数代表输入层神经元个数,列数输入训练集组数)
输入层
包含30m行进跑、立定三级跳远、助跑摸高、助跑4-6步跳高、负重深蹲杠铃、杠铃半蹲系数、100米、抓举
隐层
目前, 对于隐层中神经元数目的确定并没有明确的公式, 只有一些经验公式, 神经元个数的最终确定还是需要根据经验和多次实验来确定。本文在选取隐层神经元个数的问题上参照了以下的经验公式:
其中,n为输入层神经元个数,m为输出层神经元个数,a为【1,10】之间的常数。根据上式可以计算出神经元个数为4-13之间,在这次试验中选择隐层神经元个数为6。
激励函数选取
隐层神经元的激励函数选用S型正切函数tansig。而由于网络的输出归一到【-1,1】范围内,因此输出层神经元激励函数还是选取tansig。
模型的实现
此次预测选用MATLAB中的神经网络工具箱进行网络的训练,预测模型的具体步骤如下:
将训练样本数据归一化后输入网络,设定网络隐层和输出层激励函数分别为tansig和logsig函数,网络迭代次数epochs为5000次,期望误差goal为0.00000001,学习速率lr为0.01。
MATLAB代码部分
P=[3.2 3.2 3 3.2 3.2 3.4 3.2 3 3.2 3.2 3.2 3.9 3.1 3.2;
9.6 10.3 9 10.3 10.1 10 9.6 9 9.6 9.2 9.5 9 9.5 9.7;
3.45 3.75 3.5 3.65 3.5 3.4 3.55 3.5 3.55 3.5 3.4 3.1 3.6 3.45;
2.15 2.2 2.2 2.2 2 2.15 2.14 2.1 2.1 2.1 2.15 2 2.1 2.15;
140 120 140 150 80 130 130 100 130 140 115 80 90 130;
2.8 3.4 3.5 2.8 1.5 3.2 3.5 1.8 3.5 2.5 2.8 2.2 2.7 4.6;
11 10.9 11.4 10.8 11.3 11.5 11.8 11.3 11.8 11 11.9 13 11.1 10.85;
50 70 50 80 50 60 65 40 65 50 50 50 70 70];
?T=[2.24 2.33 2.24 2.32 2.2 2.27 2.2 2.26 2.2 2.24 2.24 2.2 2.2 2.35];
[p1,minp,maxp,t1,mint,maxt]=premnmx(P,T);
%创建网络
net=newff(minmax(P),[8,6,1],{'tansig','tansig','purelin'},'trainlm');
%设置训练次数
net.trainParam.epochs = 5000;
%设置收敛误差
net.trainParam.goal=0.0000001;
%训练网络
[net,tr]=train(net,p1,t1);
TRAINLM, Epoch 0/5000, MSE 0.533351/1e-007, Gradient 18.9079/1e-010
TRAINLM, Epoch 24/5000, MSE 8.81926e-008/1e-007, Gradient 0.0022922/1e-010
TRAINLM, Performance goal met.
%输入数据
a=[3.0;9.3;3.3;2.05;100;2.8;11.2;50];
%将输入数据归一化
a=premnmx(a);
%放入到网络输出数据
b=sim(net,a);
%将得到的数据反归一化得到预测数据
c=postmnmx(b,mint,maxt);
c
c =
2.2003结论
序号15的跳高成绩的预测结果为2.2003
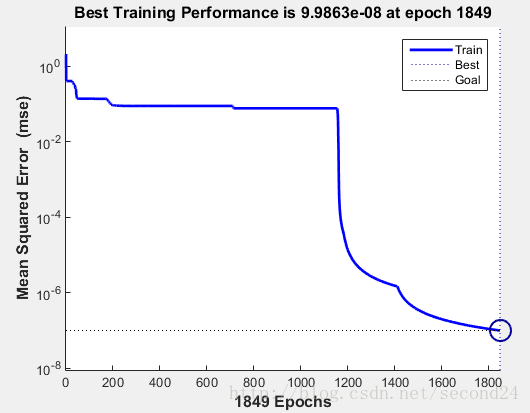
——-下图是训练过程
大致意思就是在训练次数达到1849次时的训练结果最佳。
4. 全局最小和局部极小
若用E表示神经网络在训练集上的误差,则它显然是关于连接权w和阈值theta的函数。此时,神经网络的训练过程可看作一个参数寻优过程,即在参数空间中,寻找一组最优参数使得E最小。
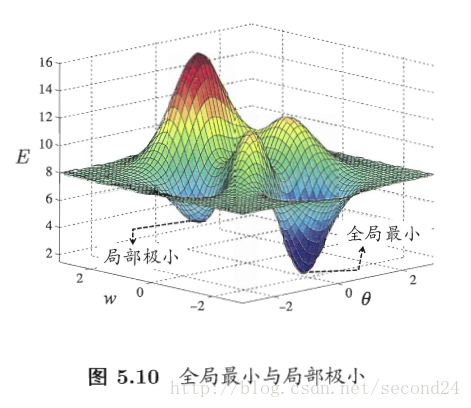
我们在参数寻优过程中是希望找到全局最小。
参数寻优方法
基于梯度的搜索是使用最广泛的参数寻优方法。在此类方法中,我们从某些初始解出发,迭代寻找最优参数值。每次迭代中,我们先计算误差函数在当前点的梯度,然后根据梯度确定搜索方向。但是,若误差函数在当前点的梯度为零,则已达到局部极小,更新量将为0,这意味着参数的迭代更新将在此停止。显然,如果误差函数仅有一个局部极小,那么此时找到的局部极小就是全局最小;然而,如果误差函数具有多个局部极小,这显然不是我们希望的。








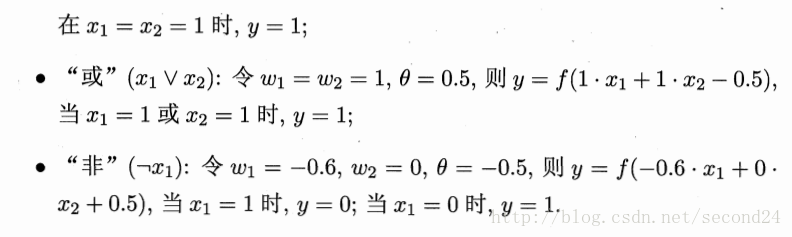

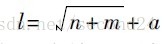


















 4814
4814

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








