论高斯消元

1前言
本文会讲解高斯消元法，保证使用初中或小学知识
用线性代数来讲就是生怕别人学会

2问题
鸡兔同笼问题
笼子里有鸡和兔，共有35个头，94只脚
求鸡和兔各有几只

3解二元一次方程组
初中数学课本教会了我们解二元一次方程组
设有x只鸡，y只兔，则有
x + y = 35
2x + 4y = 94
解法一:带入消元法
移项得x = 35 - y
带入得2(35-y) +4y = 94
70 - 2y + 4y = 94
y = 12
x = 23
解法二:加减消元法
方程1乘以2得
2x + 2y = 70
方程2减去1得
2y = 24
y = 12
x = 23
这题简单
可是如果有更多未知数，3个或者更多，怎么办
如果未知数的系数不固定，怎么办

4一般性问题

给定一个线性方程组（即n元一次方程组，因为次数为1，所以是线性的）
一般式如下

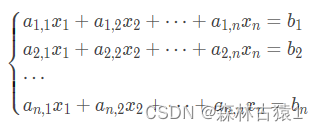
5高斯消元

我们观察上面的方法，加减消元法根本不用考虑合并同类项
写成代码可直接用数组存系数
解决普遍性问题也是更加好用的
于是，高斯消元诞生了，就是加减消元法的变形
先看定义
高斯消元法是求解线性方阵组的一种算法，它也可用来求矩阵的秩，以及求可逆方阵的逆矩阵。
它通过逐步消除未知数来将原始线性系统转化为另一个更简单的等价的系统。它的实质是通过初等行列变换，
将线性方程组的增广矩阵转化为行阶梯矩阵.

和神犇语言不通，我来翻译一下
等价，即未知数不变，也就是使最后的解带入其中可以使等式成立，再说简单点就是不出错

初等行列变换有三种
1.把某一行乘上一个非0的数
2.交换某两行
3.把某行若干倍加到另一行
这些除了2,解鸡兔同笼问题都会用到
步骤2可以很好的保持问题的一般性，为什么要保持一般性？后面会说

将线性方程组的增广矩阵转化为行阶梯矩阵，就是把原方程转化为第x列有（n-x+1）个未知数
即第一行有n个，第二行有n-1个，第n行有1个，同时保证等价于原方程组
这个过程就是把原方程变得更简单
可以发现，最后消元完成，即变为阶梯状，只需回推就行
回推时会有三种情况
1 ax = b有唯一解
2 0 = b且b为0，有无穷多解
3 0 = b且b不为0，无解
还可以判断解的情况，太好用了

6实现

目前问题是怎么将原方程组化简且保证等价性
我们可以从阶梯状入手，为什么这个算法最终是把方程变为阶梯状？
很简单，可以递推，把每一项都简化为*
首先
****
****
****
然后
****
 ***
 ***
可以发现第一行满足要求，不会影响后面的，同时，后面的也形成了一个规模为n-1的更小问题
具有无后效性，这个性质太好了
接下来再这样讲太抽象了，举个例子吧
1.00x1 + 2.00x2 - 1.00x3  = -6.00
2.00x1 + 1.00x2 - 3.00x3  = -9.00
-1.00x1 + -1.00x2 + 2.00x3 = 7.00
首先，把第一行第一项系数化为1
第一行是什么都能求解，但要尽可能少的丢失精度
因为第一行每一项都要除以第一项系数，系数越大，精度丢失越多
但是第一行先运算，将不参与后续运算
所以直接把系数最大的换到第一行
然后的步骤就简单了，遍历下面每一列，将第一行乘上一个数
1第1行第1项系数为1，设第x行第1项系数为a
则把第一行乘上-a加到第x行，消完了，就是简单
初等行列变换都用上了
最后的逆推，枚举每一行，在枚举下面的行，依次消掉这行每个系数，最后常数项为解
附流程图及代码

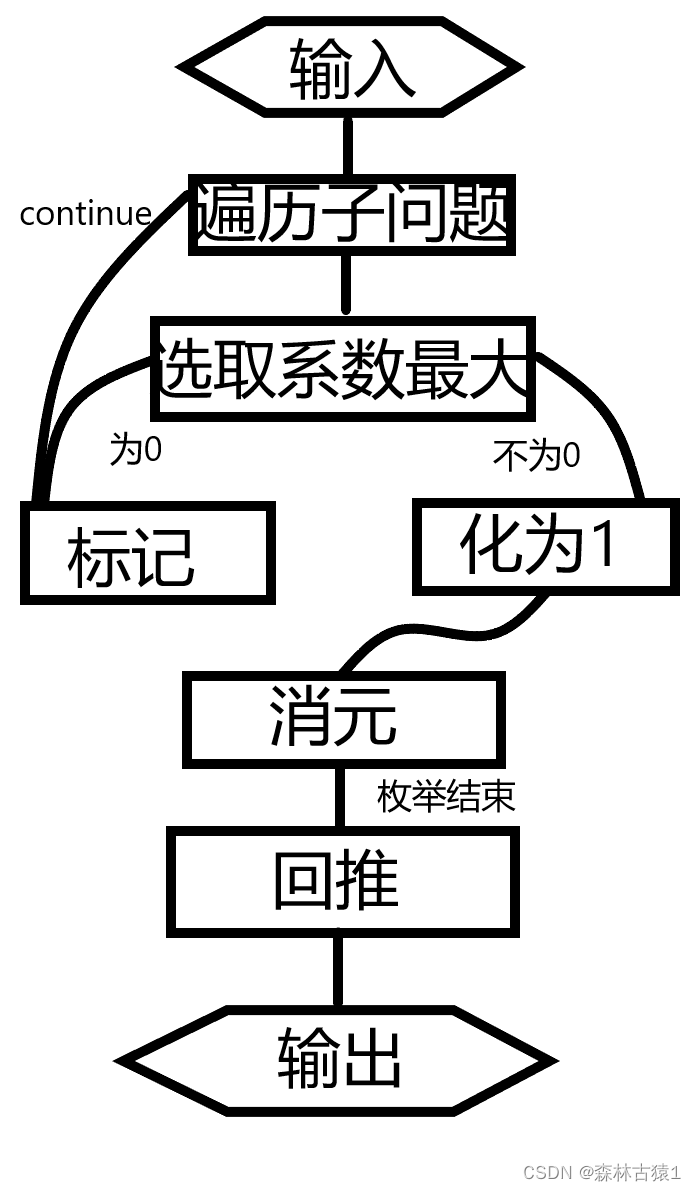
#include<bits/stdc++.h>
using namespace std;
int n;
double a[114][114];
const double MIN = 1e-8;
//初等行列变换 
void solve1(int x,int y,int o){//交换x,y两行 
	for(int i = o;i<=(n+1);i++){
		swap(a[x][i],a[y][i]);
	}
}
void solve2(int x,double k,int o){//将第x行乘以k,这里写为除 
	for(int i = n+1;i>=o;i--){
		if(fabs(a[x][i])>MIN)a[x][i]/=k;
	}
}
void solve3(int x,int y,double k,int o){//将第x行的k倍加到第y行 
	for(int i = o;i<=(n+1);i++){
		if(fabs(a[x][i])>MIN)a[y][i]+=(a[x][i]*k); 
	}
}
//高斯消元
int gauss(){
	int x,y = 1;
	for(int x = 1;x<=n;x++){
		int k = x;
		for(int i = x+1;i<=n;i++){
			if(fabs(a[i][x])>fabs(a[k][x])){
				k = i;
			}
		}
		if(fabs(a[k][x])<MIN){
			continue;
		}
		solve2(k,a[k][x],x);//系数化为1
		solve1(x,k,x);//交换 
		for(int j = x+1;j<=n;j++){
			if(fabs(a[j][x])>MIN){
				double p = -a[j][x];
				solve3(x,j,p,x);
			}
		}
		y++;
	}
	if(y<=n){
		for(int i = y;i<=n;i++){
			if(fabs(a[i][n+1])<MIN){
				return 114514;
			}
		}
		return 1;
	}
	for(int i = n;i>=1;i--){
		for(int j = i+1;j<=n;j++){
			double p = -a[i][j];
			solve3(j,i,p,x);
		}
	}
	return 0;
}
int main(){
	cin>>n;
	for(int i = 1;i<=n;i++){
		for(int j = 1;j<=(n+1);j++){
			scanf("%lf",&a[i][j]);
		}
	}
	int ans = gauss();
	if(ans==0){//唯一解 
		for(int i = 1;i<=n;i++){
			printf("%.2lf\n",a[i][n+1]);
		}
	}else if(ans==1){//无穷多解
		puts("Infinite group solutions");
	}else{//无解 
		puts("No solution");
	}
	return 0;
}

7代码注意事项
作者做本题时调了一上午
注意开double，开成int直接WA
数据可能包含0

8后记
高斯消元的应用还很多，但都是线性代数方面的，短期之内学不会，所以作者暂时不挖坑
以后有机会还是要尝试一下
本文作者是一个蒟蒻，欢迎各位大牛指点