第二章 图像、采样和频域处理 （2）

第二章 图像、采样和频域处理 （2）

2.4 采样标准

a. 采样标准对采样频率进行规定，在物理上这些值是A/D转换器对模拟信号进行采样的输出；
b. 示例采样函数：
峰值间隔为∆t 的时域等间隔脉冲；
采样过程的频域模拟是将信号频谱与采样函数的频谱进行卷积运算，即将某一个频谱沿水平轴反转，然后滑过另一个频谱；以峰值谱为例，输出为一个原信号频谱以1/∆t为周期的重复频谱；
显然过大的采样间隔会导致输出频谱周期间隔较小，信号频谱出现重叠，导致信号被破坏，为避免冲突要求采样频率超过信号频谱最大频率的2倍，2倍是实际上因为信号频谱是-fmax到fmax的；
Nyquist采样标准：为了从样本重构原信号，采样频率必须至少是被采样信号最大频率的两倍；
对于图像，低分辨率可以看成是在空间域的采样频率不足，存在真实信息的走样；有些实际上根本不存在的东西，采样的结果使它们看起来存在，也就是在信号的重构过程出现了问题，这是采样频率过低的结果（所以不推荐电视上穿格子衬衫）；
c. 更新的采样理论参考Unser(2000)，此外Donoho(2006)提出一个事实，即很多信号存在重要分量和实际上接近0的分量，导致摄像机可以通过少量重要元素近似重构图像，提供了在不降低分辨率的情形下压缩图像的另一个基准；
d. 一个技术限制的例子，上古计算机以11MHz进行采样，最大相机输出频率5.5MHz，11MHz意味着最小图像分辨率需要为576576，但这不是2的整数次幂，实际图像系统的最大分辨率为512512，因此系统必须对走样进行预测；
通过观察，以下内容可以在一定程度上降低走样：

1. 总体来看，较低频率带有更多信息，而较高频率只局部地包含较多信息，所以高频率信息被破坏不那么重要；
2. 在成像系统中，景深是有限的，减少了高频率组成；

对高频率分量的估算精度可以采用有效采样频率（图像点数）和成像结构之间的关系表示，这个基本思想仍然适用；

2.5 离散傅立叶变换

2.5.1 一维变换

a. 一组采样频率为Fpu的N个采样点px的DFT为：

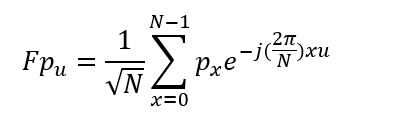
b. 将DFT应用于一个窗口中的脉冲样本（窗口脉冲，即方波），其样本从0到N/2-1则有

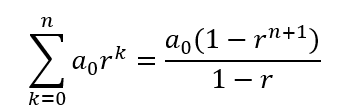
进行几何级数求和展开

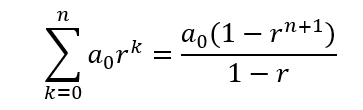
则采样脉冲的离散傅立叶变换可以表示为

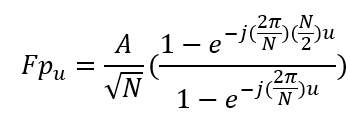
整理可得

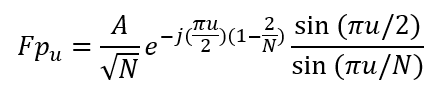
该变换的模为：

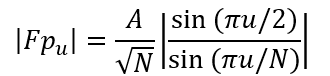
这是由于指数函数的幅度为1；
c. 根据傅立叶描述，通过将频率相加可以重构被采样脉冲，离散傅立叶变换频域系数表示原信号中对应正弦信号的数目；最低品分量为Fp0即直流分量，表示样本均值；在Fp0的基础上不断累加高阶分量Fpi可以对原信号进行逼近近似，该过程即DFT逆；它可以通过下式重构采样信号：

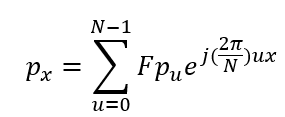
d. 在应用DFT之前需要注意假设条件：
（1）满足采样标准
（2）采样函数不断重复至无穷
（3）最大频率对应半个采样周期

2.5.2二维变换

a. 图像的DFT是具有二维空间位置的像素点（采样图像点）的变换，这些二维空间位置由坐标x和y表示，对应到频域为u和v，分别表示水平和垂直方向的空间频率；
对于一组由平行垂直线构成的图像，其垂直方向的空间频率为0；
二维傅里叶变换从NxN个像素P(x,y)计算对应的频域数据Fp(u,v)，如

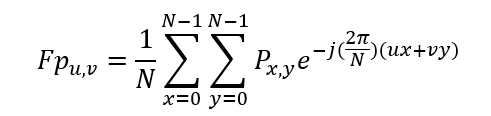
光学上，图像的傅里叶变换可以通过对一张摄影幻灯片发射激光，并利用透镜成像来得到；该幻灯片图像的傅里叶变换是在透镜前焦平面形成的，其应用仍然局限于传送式系统，而反射式构成大幅度扩展了傅里叶变换的应用潜能（因为光学计算比数字计算略快一些）；
b. 二维DFT逆

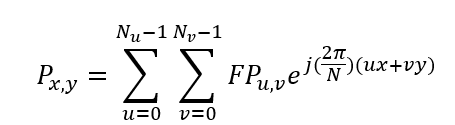
c. 傅里叶变换的重复性，意味着变换在频率上不断重复至无穷；对一维信号很容易进行描述，对二维信号通过对采样点数目进行整数倍的变换，

易见(mx+ny)是整数，所以指数项实际上是的2π整数倍，则e^(-j(2π)(mx+ny) )=1，因此

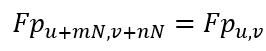
d. 对大型图像，考虑到数据量较大，通常采用快速傅里叶变换FFT实现，FFT通过对DFT进行合理分组以提高计算速度；
计算还涉及傅里叶变换的可分离性，即傅里叶变换可以分为两个阶段进行，首先利用一维FFT对行进行变换，然后再次利用一维FFT对于变换后的数据进行列变换；
则有：

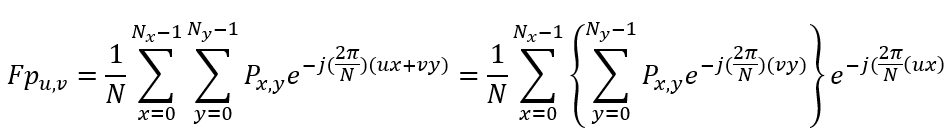
e. 计算成本：
容量为N的一维FFT计算成本为O(N log(N))；
二维FFT计算成本为O(N^2 log⁡(N))；
二维DFT计算成本为O(N^3)；
很多傅里叶变换之间的差别在于所选的比例因子不同；
f. 图像的傅里叶变换得到的是频率分量，每个分量的位置表示其频率，距离远点越近则频率越低，0频率表示直流分量；不巧的是二维傅里叶变换的布局是低频率分量处于变换的边角上，而将低频置于图像中间可以增强图像的可视性，一般通过将傅里叶变换的四个象限分别旋转180°或者将原图重新平移排列，对应的频域分量需要进行重新排序，将每个图像点的P(x,y)与-1^(x+y)相乘，又cos⁡(-π)=-1=e^(-jπ)，则图像变换为

g. 二维傅里叶变换对：二维脉冲-二维sinc函数；二维高斯函数-二维高斯函数；

2.6 傅里叶变换的其他特性

2.6.1 位移不变性

a. 图像分解为空间频率与特征在图像中的位置无关；
把p(t)的延迟形式记为p(t-τ)，其中τ表示延迟，位移后图像的傅里叶变换记为ς[p(t-τ)]，则时域位移和频域之间的关系为

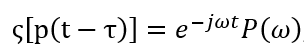
如果指数函数的幅度为1.0，那么位移后图像的傅里叶变换幅度与原图像相等；
b. 位移后傅里叶变换的相位产生变化;

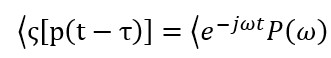
根据傅里叶变换的这一特性，可以避免特征空间位置的影响；

2.6.2 旋转

a. 傅里叶变换处理具有朝向依赖性；这意味着如果通过傅里叶变换将频域特性用于图像分析，那么朝向必须已知或者固定；特征的朝向通常可以固定，否则需要推测朝向参数；此外可以通过转换为极坐标表示等方法消除图像旋转的影响；

2.6.3 频率尺度变化

a. 图像压缩则频率响应增大，频域分量存在扩展；即有

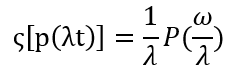
2.6.4 叠加

a. 叠加原理表示为O(I1+I2 )=O(I1 )+O(I2)，任何满足叠加原理的系统都被看做是线性的；
傅里叶变换是一个线性系统，对信号p1和p2有

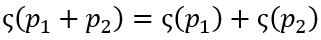
2.7 傅里叶变换以外的其他变换

2.7.1 离散余弦变换

a. 实数变换，在能量集中性方面具有很大优势；

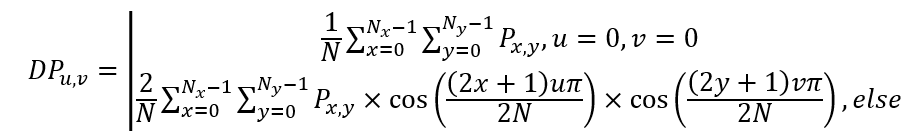
离散余弦变换的逆：
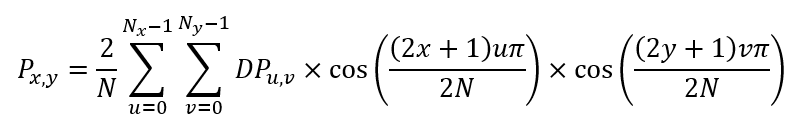与传统的傅里叶变换对比，DCT对相同要求的图像可以给出更高的压缩率，因此更适用于图像压缩；
b. DCT随余弦基函数而位移变化；DCT与DFT非常相似，但还没有证实DCT可以实现卷积运算；

2.7.2 离散Hartley变换

a. 是傅里叶变换的一种不需要复数计算的形式；Hartley变换的优势是正变换和逆变换进行的是相同的操作；DHT定义如下，

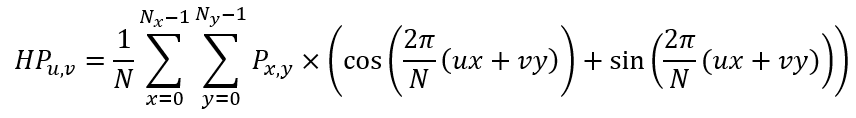
离散Hartley变换的逆，

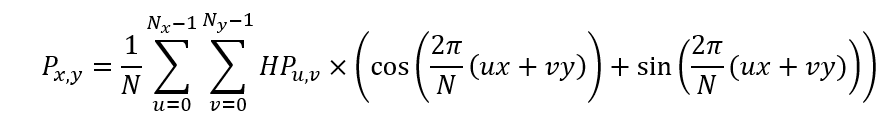
b. 快速Hartley变换
根据函数的Hartley变换H(u)可以计算函数F(u)的DFT，以一维为例，将Hartley变换分解为奇部和偶部，则有H(u)=O(u)+E(u)，其中E(u)=(H(u)+H(N-u))/2，O(u)=(H(u)-H(N-u))/2，则DHT可以简单计算为F(u)=E(u)-j×O(u),
同理，Hartley变换也可以通过傅里叶变换计算，H(u)=Re[F(u)]-Im[F(u)]；
Hartley变换没有位移不变性（可以通过一些办法进行处理），且其卷积需要注意奇部和偶部的问题；

2.7.3 小波简介

2.7.3.1 Gabor小波

a. 小波是一种比较新的信号处理方法，主要优势是可以进行多分辨率分析；小波可以同时进行时域和频域的采样，具有更强的描述能力；
b. 基函数，Gabor小波采用的基函数是高斯包络调制的正弦波，

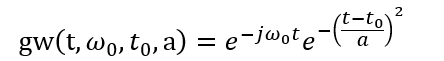
其中ω0=2πf0表示调制频率，t0表示位置，a控制高斯包络形状；
c. 二维Gabor小波计算，

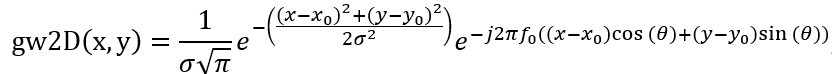
其中x0，y0控制位置，f0控制任一轴的调制频率（即x方向和y方向的频率实际上可以不同），θ控制小波方向；若x和y方向参数不同（包括频率）则其二维高斯函数形状近似椭圆；
d. 离散小波变换不具有平移不变性；

2.7.4 其他变换

a. Haar小波变换；
b. Walsh变换；
c. Karhumen-Loeve变换；