第七届蓝桥杯C/C++B组省赛部分题目

6.方格填数
如下的10个格子
   +--+--+--+
   |  |  |  |
+--+--+--+--+
|  |  |  |  |
+--+--+--+--+
|  |  |  |
+--+--+--+


（如果显示有问题，也可以参看下图）




填入0~9的数字。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）

一共有多少种可能的填数方案？

请填写表示方案数目的整数。

注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

思路：我是按照0-9数字不重复来算的，给位置标号，依次为对应数组里元素a[0]~a[9],然后全排列，生成后判断是否满足条件即可

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int ans=0;
int a[10]={0,1,2,3,4,5,6,7,8,9};

int match(){
	for(int i=0;i<=8;i++){
		if(i == 6 || i == 2) continue;
		if(abs(a[i]-a[i+1])==1) return 0;
	} //判断前后
	for(int i=0;i<=5;i++){
		if(abs(a[i]-a[i+4])==1) return 0;
	}  //判断上下
	for(int i=0;i<=6;i++){
		if(i == 3 ) continue;
		if(abs(a[i]-a[i+3])==1) return 0;
	}   //判断对角线
	for(int i=0;i<=4;i++){
		if(i == 2) continue;
		if(abs(a[i]-a[i+5])==1) return 0;
	}  //判断对角线  不同的方向，当时考场里忘写这条了。。
	return 1;
}

void dfs(int k){
	if(k>=10){	
//		for(int i=0;i<10;i++){
//			cout<<a[i]<<" ";
//		}
//		cout<<endl;
		if(match() == 1){
			ans++;
		}
		return ;
	}
	for(int i=k;i<10;i++)
	{
		int temp;
		temp=a[k];a[k]=a[i];a[i]=temp;
		dfs(k+1);
		temp=a[k];a[k]=a[i];a[i]=temp;
	}
} 

int main()
{
	dfs(0);
	cout<<ans<<endl;
	return 0;
}

然后这题的答案是 1580

8.四平方和
四平方和定理，又称为拉格朗日定理：
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去，就正好可以表示为4个数的平方和。

比如：
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2
（^符号表示乘方的意思）

对于一个给定的正整数，可能存在多种平方和的表示法。
要求你对4个数排序：
0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列，最后输出第一个表示法

程序输入为一个正整数N (N<5000000)
要求输出4个非负整数，按从小到大排序，中间用空格分开

例如，输入：
5
则程序应该输出：
0 0 1 2

再例如，输入：
12
则程序应该输出：
0 2 2 2


再例如，输入：
773535
则程序应该输出：
1 1 267 838

资源约定：
峰值内存消耗 < 256M
CPU消耗  < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>， 不能通过工程设置而省略常用头文件。

思路：比赛时候直接四重循环，优化了一点，应该可以过部分数据，毕竟3000ms。。。

以下为别人的优化思路

1.第四重循环不写，直接判断剩下的数是否为一个整数的平方数。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int main()
{
	long long int m;
	cin>>m;
	int n = sqrt(m);
	for(int i=0;i<=n+1;i++)
	{
		for(int j=i;j<=n+1;j++)
		{
			for(int k=j;k<=n+1;k++)
			{
				int temp=m-i*i-j*j-k*k;
				double s = sqrt(temp);
				if(s == (int)s)
				{
					cout<<i<<" "<<j<<" "<<k<<" "<<(int)s<<endl;
					return 0;
				}		
			}		
		}	
	} 
	return 0;
}

2.在第一种的情况下，开一个大数组存储这个数是否可以表示为一个数的平方数。

#include <stdio.h>
#include <math.h>
int mpt[5000010] ={0};//mpt[100]=1  表示100可以被表示为一个整数的平方数
int n;
void init()
{
    for(int i = 0 ; i*i <= n ; i ++)
        for(int j = 0 ; j*j <=n ; j ++)
            if(i*i+j*j <= n) mpt[i*i+j*j] = 1;
}
int main()
{
    int flag = false;
    scanf("%d",&n);
    init();
    for(int i = 0 ; i * i <= n ; i ++)
    {
        for(int j = 0 ; j * j <= n ; j ++)
		{
            if(mpt[n - i*i - j*j] == 0) continue;//这条语句重点优化 
            for(int k = 0 ; k * k <= n ; k ++)
            {
                int temp = n - i*i - j*j - k*k;
                double l = sqrt((double) temp);
                if(l == (int)l)
                {
                    printf("%d %d %d %d\n",i,j,k,(int)l);
                   	return 0;                    
                }
            }
        }
    }
    return 0;
}

7.剪邮票
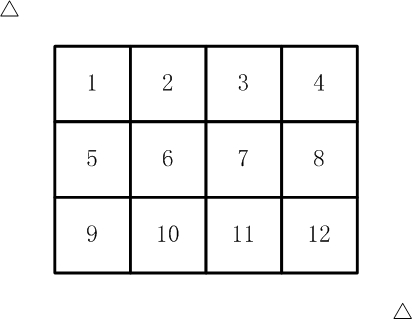
如【图1.jpg】, 有12张连在一起的12生肖的邮票。


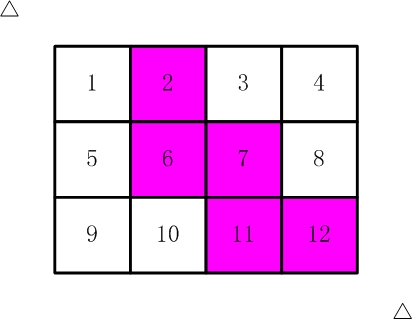
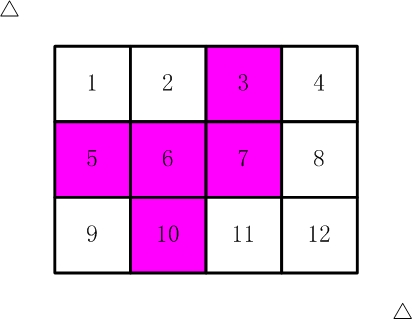
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。


请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。


其实这个题目还是可前面的一样,先生成,再判断是否可行。这里我们可以先用搜索从12个数里面将所有5个数的组合找出来。然后再用深搜判断这五个是否连在一起。答案是：116

#include <stdio.h>
#include <string.h>
int mpt[3][4];
int mpt_visit[3][4];
int num[6];
int have[13];
int visit[13];
int ans = 0;
int Count = 0;

void init()//初始化数组 
{
    int k = 1;
    for(int i = 0 ; i < 3 ; i ++)
        for(int j = 0 ; j < 4 ; j ++)
        {
            mpt[i][j] = k;
            k ++;
        }
}
int dir[4][2] = {0,1,0,-1,-1,0,1,0};
//判断五个数是否能连在一起
//深度搜索 
void dfs_find(int x,int y)
{
    for(int i = 0 ; i < 4 ; i++)//四个方向遍历 
    {
        int tx,ty;
        tx = x + dir[i][0];
        ty = y + dir[i][1];
        if(tx < 0 || tx >= 3 || ty < 0 || ty >= 4) continue;//是否越界，越界下一个 
        if(have[mpt[tx][ty]] == 0 || mpt_visit[tx][ty])continue;//该点是否被选中；该点是否访问过 
        mpt_visit[tx][ty] = 1;//标记为访问过 
        Count ++;//邮票数+1 
        dfs_find(tx,ty);//继续搜索 
    }
}

void Solve()
{
    int i;
    memset(have,0,sizeof(have));//
    memset(mpt_visit,0,sizeof(mpt_visit));
    for(i = 1; i < 6 ; i ++) have[num[i]] = 1;//选中的数字标记下 
    for(i = 0 ; i < 12 ; i ++)
    {
        int x,y;
        x = i / 4;
        y = i % 4;
        if(have[mpt[x][y]])
        {
            Count = 1;
            mpt_visit[x][y] =1;
            dfs_find(x,y);//判断这些点是否连通 
            break;
        }
    }
    if(Count == 5)
    {
        ans ++;
    }
}

//创建5个数的组合
void dfs_creat(int index)//十三选5个   不重复的数字，然后判断是否连通 
{
    if(index == 6)
    {
        Solve();
        return;
    }
    for(int i = num[index-1] + 1; i < 13 ; i ++)
    {
        if(!visit[i])
        {
            visit[i] = true;
            num[index] = i;
            dfs_creat(index+1);
            visit[i] = false;
        }
    }
}

int main()
{
    init();
    dfs_creat(1);
    printf("%d\n",ans);
    return 0;
}

有的代码来自

http://blog.csdn.net/hurmishine/article/details/50950944

http://blog.csdn.net/y1196645376/article/details/50938608