安全多方计算——Yao‘s 混淆电路

Yao’s混淆电路

   姚期智院士提出的首个安全多方计算方案，该方案可以计算任意可以转换成电路的函数f(x),属于安全双方计算方案。安全思想：一个人加密整个电路的输入输出，另一个人盲算，这样就导致信息不对称，从而一方不能获得另一方的数据。

   以加密一个与门G为例。该与门有两个输入A,B；一个输出Y。

与门G

   假设Alice与Bob要计算这样的一个与门G，Alice拥有输入A的值，Bob拥有输入B的值，他们要各自用自己的数据做“与运算”。

方案如下：

1. Alice为输入和输出每个可能的值创建一个标签，分别为 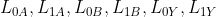。 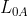表示当A取0时生成的标签， 表示当A取1时生成的标签，其他类似。

2. Alice使用输入标签作为密钥将输出标签进行加密生成一个加密的真值表。

在这个表中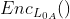，表示使用标签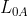作为密钥进行对称加密,其他类似。

Alice再将这个表的位置进行随机置换就得到了混淆表。

3. Alice将混淆表和自己的输入所对应的标签发送给Bob。

4. Bob运用不经意传输协议（OT）向Alice请求自己的输入对应的标签。这样Bob就得到了解密输出标签所需要的全部两个标签。

5. Bob使用两个标签对混淆表解密，最终只有一行可以成功解密，这个结果就是与运算的输出标签，将标签发送给Alice。Alice将最后的真实结果告诉Bob。

关于混淆电路的一些解释：

第一点： 标签只是一些随机数，标签其实就代表了某根导线的取值（0或1）。

第二点：不经意传输协议可以做到：Bob可以向Alice请求自己的输入对应的标签，但Alice并不知道Bob最后请求的是哪个标签。

第三点： 上述方案只是一个与门的例子，如果只计算这么一个门，那么一方可以根据自己的输入和最终结果推出另一方的输入。实际中的电路是由很复杂的各种门组合而成，在这样的电路中，一方是不会反推出另一方的输入的。

第四点：在较复杂的电路里，Alice是对电路中每一根导线都设定两个标签，对每个门都生成一张混淆表。这里的导线可能同时是一个门的输出和另一个门的的输入，这时候，导线作为门输出的两个标签和作为门输入的两个标签是对应一样的。所以在Bob的计算过程中，Bob始终不知道Alice的输入是什么（他只知道Alice输入的标签，但不知道标签对应的真实值是什么。换句话说，Bob可以完成整个计算，但是Bob计算的都是一些标签值，他并不知道这些标签所对应的真实值，所以他不能推出Alice的输入）。而Alice虽然知道每个标签所代表的真实值，但是他全程都没有参与计算，所以并不能知道中间结果，也就不能推出Bob的输入

第五点：这一点我没有想明白，如果有大佬知道，请在评论区告诉我，不胜感激！！Bob用两个标签解密时会对混淆表的四行都尝试解密，只有一个会解密成功，那么它是如何判定某一行是解密成功的呢？毕竟都是一些看似是乱码的随机数。（PS：这个问题在一些Yao’s混淆电路优化方案中被得到优化，有一个方案大概是生成混淆表时把对应位置也记录下来，这样只要解密特定位置的行就可以了，这样就减少了计算开销。）