0-1背包问题多算法求解问题

一、问题分析。
1、问题内容：给定n种物品和一个背包。物品i的重量是Wi，其价值为Vi，背包最大承载重量为C。物品是不可分割的，应如何选择装入背包的物品，使得装入背包中物品的总价值最大?
2、要求：随机生成物品和背包数据。至少用三种(回溯、分支限界、动态规划等)以上不同算法求解并比较各种算法的优劣。
二、问题的解决方案/算法选择/设计思路。
背包问题主要包括0-1背包问题和部分背包问题如图2-1。其中0 - 1背包问题可以用动态规划算法、回溯算法。部分背包问题可以用贪心算法。

 

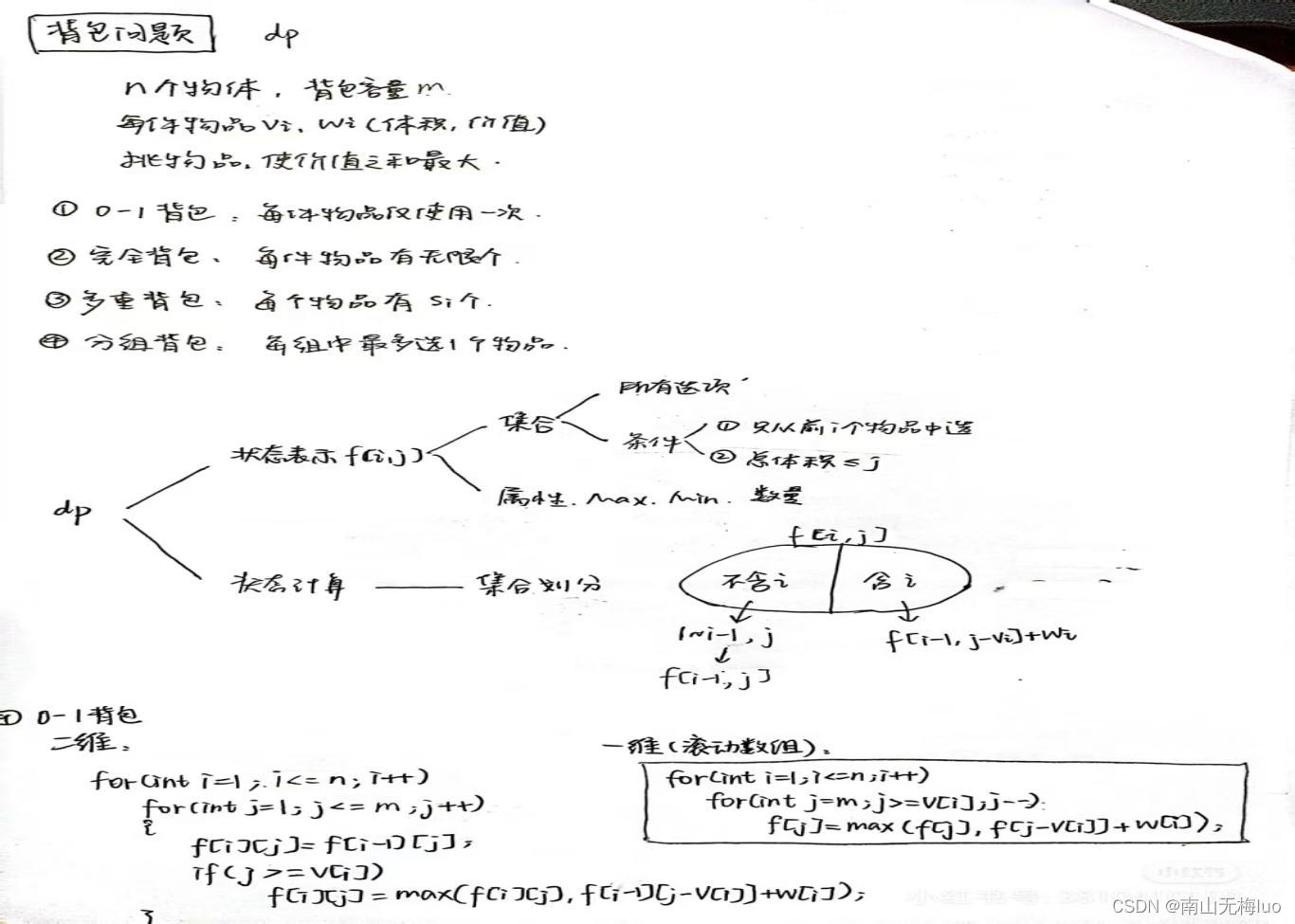
图2-1
动态规划算法求解0-1背包问题，它适用于解决物品不能分割的情况。其核心思想是通过构建一个二维数组（设为dp[i][j]，其中i表示考虑到第i个物品，j表示背包容量）来记录每个子问题的最优解。例如：有5个物品和容量为10的背包。dp[3][7]就表示考虑前3个物品放入容量为7的背包时的最优解。状态转移方程通常是dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])，其中w[i]是第i个物品的重量，v[i]是其价值。优点是能得到全局最优解，对于小规模问题效率高如图2-2。缺点是空间复杂度和时间复杂度相对较高，空间复杂度通常是O(n * m)，时间复杂度也是O(n * m)，n是物品数量，m是背包容量。

 

图2-2
（2）回溯算法求解0-1背包问题，它通过搜索所有可能的物品组合来找到最优解。思路是从第一个物品开始，依次考虑放入或不放入背包，然后递归地处理下一个物品。比如，先考虑第一个物品放进去背包后的情况，再考虑不放的情况，然后对第二个物品也这样递归操作。优点是能够找到所有可能的解，对于简单的小问题比较直观。缺点是效率较低，时间复杂度是指数级别的O(2^n)，因为每个物品都有放和不放两种选择如图2-3。

 

图2-3
贪心算法求解部分背包问题，因为部分背包问题允许物品可以分割，所以贪心算法比较适用。其思路是按照物品的价值重量比（v[i]/w[i]）进行排序，优先选择价值重量比高的物品放入背包，直到背包无法再放入完整的物品，再将最后一个物品按剩余空间的比例分割放入。例如，有三个物品A、B、C，价值重量比分别为3、2、1。先尽可能多地放入A，然后放B，最后放C。优点是简单高效，时间复杂度通常为O(nlogn)（主要是排序的时间）。缺点是只能用于部分背包问题这种可以分割物品的情况，对于0 - 1背包问题不能保证得到最优解如图2-4。

 

图2-4
三、算法设计/问题求解中所遇到的问题及分析解决方案；
1.时间复杂度问题
（1）问题描述：
在背包问题求解过程中，如使用暴力解法（对于0 - 1背包问题，遍历所有可能的物品组合）或简单的递归方法，时间复杂度会非常高。例如，对于包含n个物品的0 - 1背包问题，暴力解法的时间复杂度为O(2^n)，当n较大时，计算时间会呈指数级增长，导致程序运行效率极低。
（2）解决方案分析：
a、动态规划：通过记录子问题的解来避免重复计算。例如，在0 - 1背包问题中，构建一个二维数组dp[i][j]，其中i表示考虑到第i个物品，j表示背包容量。在计算dp[i][j]时，可以利用之前计算的dp[i - 1][j]和dp[i - 1][j - w[i]]（w[i]为第i个物品重量）的值，这样时间复杂度可以降低到O(n * m)，n是物品数量，m是背包容量。
b、贪心算法（适用于部分背包问题）如图3-1：按照一定的贪心策略（如价值重量比）选择物品放入背包。这样可以在O(nlogn)时间内（n为物品数量，主要时间花费在排序上）得到一个较优解，大大提高了效率。

 

图3-1
2、空间复杂度问题
（1）问题描述：
动态规划方法虽然降低了时间复杂度，但可能会占用较多的空间。例如，上述二维数组dp[i][j]的空间复杂度为O(n * m)。当物品数量和背包容量都很大时，会占用大量内存。
（2）解决方案分析：
优化空间复杂度：可以发现dp[i][j]的计算通常只依赖于dp[i - 1][j]和dp[i - 1][j - w[i]]，所以可以将二维数组压缩为一维数组。通过从背包容量最大值倒序遍历到0，这样可以避免使用二维数组存储所有状态，将空间复杂度降低到O(m)。
3、无法得到最优解问题
（1）问题描述：
在部分背包问题中如果错误地使用不适合的算法（如在应该用贪心算法时使用了只能解决0 - 1背包问题的动态规划），或者在0 - 1背包问题中没有考虑所有可能的组合（如使用贪心算法），会导致无法得到最优解。
（2）解决方案分析：
正确选择算法：根据背包问题的类型选择合适的算法。对于0 - 1背包问题，动态规划是可以得到最优解的有效方法；对于部分背包问题，贪心算法可以高效地得到最优解。
验证算法有效性：对于复杂的边界情况或特殊的物品属性（如物品价值和重量的关系复杂），可以通过小规模的测试数据来验证算法是否能得到最优解，并且对算法进行适当调整。
四、算法设计/问题求解特色及关键技术。
以下是0-1背包问题动态规划算法关键部分源代码
def   knapsack_01(weights, values, capacity):
n=len(weights)
#创建二维数组dp，初始化为0
dp = [[0] * (capacity + 1) for _ in range(n + 1)]

for  i in range(1, n + 1):
for j in range(1, capacity + 1):
if weights[i - 1] <= j:
# 状态转移方程，选择放入或不放入当前物品的较大价值
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1])
else:
dp[i][j] = dp[i - 1][j]
return dp[n][capacity]
以下是部分背包用贪心算法关键部分源代码
def   knapsack_fractional(weights, values, capacity):
n = len(weights)
# 计算每个物品的价值重量比
ratios = [(values[i] / weights[i], i) for i in range(n)]
# 按照价值重量比从高到低排序
ratios.sort(reverse=True)
total_value = 0
for ratio, i in ratios:
if   weights[i] <= capacity:
total_value += values[i]
capacity -= weights[i]
else:
total_value += ratio * capacity
break
return total_value;

以下是用回溯算法关键部分源代码

五、算法测试与应用。
1、背包问题算法测试
（1）测试数据准备：
a、对于0 - 1背包问题，要生成不同规模的物品数据集，包括物品的重量、价值等属性。比如，可先从小规模的几组数据开始，如5个物品、10个物品等，逐步增加到大规模数据，像100个、500个物品等。同时设定不同的背包容量值。
b、对于部分背包问题，除了物品的重量、价值，还需考虑能生成可分割的物品情况，同样准备不同规模的数据。
(2）测试用例设计：
a、功能测试：确保算法能正确处理各种输入情况。比如，输入空的物品列表时，算法应返回合适的结果（通常是0，表示无法装入物品获得价值）。输入只有一个物品的情况，算法也应准确算出该物品能否装入背包及相应价值。
b、边界条件测试：测试背包容量为0、物品重量或价值为0等边界情况。例如，当背包容量为0时，无论有多少物品，装入背包的价值都应为0；当某个物品重量为0但价值不为0，算法应能正确处理这种特殊情况。
c、性能测试：使用大规模数据测试算法的运行时间和空间占用情况。对比不同算法（如0 - 1背包问题的动态规划算法和回溯算法，部分背包问题的贪心算法等）在相同规模数据下的性能表现，看哪种算法在时间复杂度和空间复杂度上更优。
2.测试执行与结果分析：
（1）执行测试用例，记录每个测试用例的运行结果，包括算法输出的装入背包的价值、运行时间、占用的空间等信息。
（2）分析结果，检查是否有与预期不符的情况。若功能测试结果不符合预期，需检查算法逻辑是否有误；若性能测试中发现某个算法运行时间过长或空间占用过大，可考虑对算法进行优化，如对0 - 1背包问题的动态规划算法优化空间复杂度等。
3、背包问题算法应用
1.、资源分配场景应用：
（1）在企业资源分配中，如一家制造企业要在有限的资金和设备资源下选择生产哪些产品能获得最大利润。把资金看作背包容量，不同产品的生产成本看作物品重量，产品的预期利润看作物品价值，通过背包问题算法（如0 - 1背包问题的动态规划算法）可确定最优的产品生产组合。
（2）在能源分配领域，电力公司要在发电能力和输电线路容量有限的情况下，将电能分配到不同区域以满足需求并最大化效益。把输电线路容量和发电能力看作背包容量，不同区域的用电需求看作物品重量，区域的用电效益看作物品价值，运用背包问题算法来规划分配方案。
2.、物流运输应用：
（1）物流公司要在货车载重和容积有限的情况下，选择装载哪些货物能使运输价值最大。将货车的载重和容积看作背包容量，不同货物的重量和体积看作物品重量，货物的运输价值（如运费收入等）看作物品价值，利用背包问题算法（如0 - 1背包问题的动态规划算法或部分背包问题的贪心算法，根据货物是否可分割情况）来确定装载方案。
（2）在快递配送场景，快递员要在配送车辆载重和容积有限的情况下，选择配送哪些包裹能完成最多配送任务且满足客户需求。把车辆载重和容积看作背包容量，不同包裹的重量和体积看作物品重量，包裹的重要性或送达时间要求等因素可转化为物品价值，通过背包问题算法来规划配送方案。
3.投资决策应用：
（1）投资者在有限的资金下，要选择投资哪些项目能获得最大回报。把资金看作背包容量，不同项目的投资金额看作物品重量，项目的预期回报看作物品价值，运用背包问题算法（如0 - 1背包问题的动态规划算法）来确定最佳投资组合。
（2）在风险投资中，还要考虑项目的风险因素，可将风险程度转化为对项目价值的影响，然后再通过背包问题算法来做出更合理的投资决策。
六、结论
研究背包问题的过程中，仿佛踏入了一座充满挑战与惊喜的数学迷宫，每一步探索都带来深刻的感悟与收获。背包问题在众多实际领域的广泛应用更是让我惊叹于数学抽象与现实世界的紧密联系。从物流运输的货物装载到企业生产的资源配置，从个人旅行的行李打包到金融投资的项目选择，它无处不在。这充分彰显了基础算法研究的深远意义和强大生命力，看似抽象的数学模型能够为解决实际问题提供精准有效的指导，如同物理学定律支配着万物的运动一样，数学模型也在默默地塑造和优化着我们的生活与经济活动。总之，背包问题不仅仅是一个算法问题，更是一座培养思维能力、提升问题解决技巧的宝库。它教会我在面对复杂抉择时，权衡利弊、全面思考、灵活应变，并深刻理解不同策略在不同情境下的适用性。