算法导论--学习笔记017

最新推荐文章于 2021-08-30 09:41:59 发布

沈万三gz

最新推荐文章于 2021-08-30 09:41:59 发布

阅读量660

点赞数

分类专栏： C/C++ 计算机基础数据结构/算法 linux/unix

linux/unix 同时被 3 个专栏收录

719 篇文章 7 订阅

订阅专栏

计算机基础

604 篇文章 8 订阅

订阅专栏

C/C++

579 篇文章 5 订阅

订阅专栏

1.前缀编码可以保证解码唯一

0：转向左子结点

1：转向右子节点

2.平摊分析----不涉及到每一种操作的概率，旨在说明整体操作的平均代价最小，这样有助于优化设计。

在计算机科学中，特别是算法分析中，平摊分析寻找在最坏情况下的操作序列中每操作的平均耗费时间。平摊分析只保证最坏情况性能的每操作耗费时间，不涉及平均情况性能。

这个方法需要知道操作序列中可能发生的每个操作。通常应用在操作间存在状态的数据结构中。基本思想是一个最坏情况操作会改变状态从而不会在一段时间内再次出现，因此"平摊"它的耗费。

平摊分析中几种常用的技术:

聚合分析决定 n 个操作序列的耗费上界 T(n)，然后计算平均耗费为 T(n) / n。
记账方法确定每个操作的耗费，结合它的直接执行时间及它在对运行时中未来操作的影响。通常来说，许多短操作增量累加成"债"，而通过减少长操作的次数来"偿还"。
势能方法类似记账方法，但通过预先储蓄"势能"而在需要的时候释放。

B-树

是一种多路搜索树（并不是二叉的）：

1.定义任意非叶子结点最多只有M个儿子；且M>2；

2.根结点的儿子数为[2, M]；

3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

5.非叶子结点的关键字个数=指向儿子的指针个数-1；

6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的

子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

8.所有叶子结点位于同一层；

------------------------------------------我是分割线--------------------------------------

关键字数最小度数 t

1.每个非根的结点必须至少有t-1个关键字，每个非根的内结点至少有t个子女

2.每个结点可包含至多2t-1个关键字，所以一个内结点至多可有2t个子女

搜索：多路（二叉树两路分支）

插入：插入到2t-1个叶结点中，出现2t个结点后，将结点分裂成两个t

B+树

B+树是B-树的变体，也是一种多路搜索树：

1.其定义基本与B-树同，除了：

2.非叶子结点的子树指针与关键字个数相同；

3.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树

（B-树是开区间）；

5.为所有叶子结点增加一个链指针；

6.所有关键字都在叶子结点出现；

小结

B树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于

走右结点；

B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键

字范围的子结点；

所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点

中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率

从1/2提高到2/3；

---------------------------------------我是分割线-------------------------------------------------------------

二项树递归定义如下：

度数为0的二项树只包含一个结点
度数为k的二项树有一个根结点，根结点下有 $k$ 个子女，每个子女分别是度数分别为 $k-1, k-2, ..., 2, 1, 0$ 的二项树的根

二项树（从左至右度数分别为0至3

度数为k的二项树共有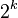 $2^k$ 个结点，高度为 $k$ 。在深度d处有 $\tbinom n d$ （二项式系数）个结点。

度数为k的二项树可以很容易从两颗度数为k-1的二项树合并得到：把一颗度数为k-1的二项树作为另一颗原度数为k-1的二项树的最左子树。这一性质是二项堆用于堆合并的基础。

二项堆

二项堆是指满足以下性质的二项树的集合：

每棵二项树都满足最小堆性质，即结点关键字大于等于其父结点的关键字
不能有两棵或以上的二项树有相同度数（包括度数为0）。换句话说，具有度数k的二项树有0个或1个。

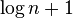以上第一个性质保证了二项树的根结点包含了最小的关键字。第二个性质则说明结点数为 $n$ 的二项堆最多只有 $\log{n} + 1$ 棵二项树。实际上，包含n个节点的二项堆的构成情况，由n的二进制表示唯一确定，其中每一位对应于一颗二项树。例如，13的二进制表示为1101, $2^3 + 2^2 + 2^0$ , 因此具有13个节点的二项堆由度数为3, 2, 0的三棵二项树组成：

示例：一个含13个结点的二项堆

二项堆的操作

由于并不需要对二项树的根结点进行随机存取，因而这些结点可以存成链表结构。

合并

合并度数相同的二项树

合并两个二项堆示例，实际上把两棵度数为1的二项树合并为一棵度数为2的二项树。

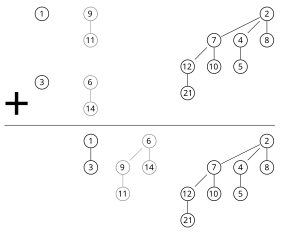
最基本的为二个度数相同的二项树的合并。由于二项树根结点包含最小的关键字，因此在二颗树合并时，只需比较二个根结点关键字的大小，其中含小关键字的结点成为结果树的根结点，另一棵树则变成结果树的子树。

function mergeTree(p, q)
    if p.root <= q.root
        return p.addSubTree(q)
    else
        return q.addSubTree(p)

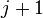两个二项堆的合并则可按如下步骤进行：度数 $j$ 从小取到大，在两个二项堆中如果其中只有一棵树的度数为 $j$ ，即将此树移动到结果堆，而如果只两棵树的度数都为 $j$ ，则根据以上方法合并为一个度数为 $j+1$ 的二项树。此后这个度数为 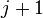$j+1$ 的树将可能会和其他度数为 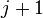$j+1$ 的二项树进行合并。因此，对于任何度数j，可能最多需要合并3棵二项树。

此操作的时间复杂度为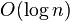 ${O}(\log n)$ 。

function merge(p, q)
    while not (p.end() and q.end())
        tree = mergeTree(p.currentTree(), q.currentTree())
        
        if not heap.currentTree().empty()
            tree = mergeTree(tree, heap.currentTree())
        
        heap.addTree(tree)
        heap.next(); p.next(); q.next()

插入

创建一个只包含要插入元素的二项堆，再将此堆与原先的二项堆进行合并，即可得到插入后的堆。由于需要合并，插入操作需要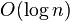 ${O}(\log n)$ 的时间。实际上需要 ${O}(1)$ 的时间

查找最小关键字所在结点

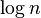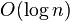由于满足最小堆性质，只需查找二项树的的根结点即可，因为一共有 $\log n$ 棵子树，所以用所时间为 ${O}(\log n)$ 。

可以保存一个指向最小元素的指针，使得查找最小关键字所在结点需要 ${O}(1)$ 的时间。在执行其他操作时，需要修改该指针。

删除最小关键字所在结点

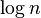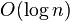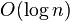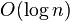先找到最小关键字所在结点，然后将它从其所在的二项树中删除，并获得其子树。将这些子树看作（合并为）一个独立的二项堆，再将此堆合并到原先的堆中即可。由于每棵树最多有 $\log n$ 棵子树，创建新堆的时间为 ${O}(\log n)$ 。同时合并堆的时间也为 ${O}(\log n)$ ，故整个操作所需时间为 ${O}(\log n)$ 。

function deleteMin(heap)
    min = heap.trees().first()
    for each current in heap.trees()
        if current.root < min then min = current
    for each tree in min.subTrees()
        tmp.addTree(tree)
    heap.removeTree(min)
    merge(heap, tmp)