L2 norm就是欧几里德距离
L1 norm就是绝对值相加,又称曼哈顿距离
搞统计的人总是喜欢搞什么“变量选择”,变量选择实际上的 限制条件是L0 Norm,但这玩艺不好整,于是就转而求L1 Norm(使用均方误差,就是Lasso ,当然在Lasso出来之前搞信号处理的就有过类似的工作),Bishop在书里对RVM好一通 吹牛,其实RVM只是隐含着去近似了一个L0 Norm, 所以得到了比SVM更稀疏的解(Tipping 写了RVM后不久就指出来了,可Bishop就是只字不提,好像贝叶斯推理有多牛,其实很多问 题 都被掩盖了起来,指望一种理论解释所有的现象总是很危险的)。最近Bin Yu给了关于La sso一致性的几乎充要条件。 SVM方面也搞了很多L1 Norm方面的东西(就是Hinge Loss在加个L1 Norm做正则化项)。 关于L1 Norm的正则化能产生稀疏解听到过个很形象地解释,那个图(L1 Norm就是个菱 形,L2 Norm是个圆)大家都看过吧,似然度(目标函数里的误差项)是个圆,求解的时候 就是拿这个圆往那个菱形(L1 Norm)圆(L2 Norm)上扔,L1的话就很可能撞到角上,所 以就稀疏了(上面是2维的情况,推广的多维就更容易撞到角上)。但如果这些变量高度相 关呢?那似然度就不是个球了,可能是个椭球,还有可能是个非常非常扁的家伙,这次再 扔就可能和正则化项很大一片都接触到了,这时候就很危险了,就果拟合了,如果数据少 ,那么这时就算是做交叉验证、留一也都无法避免过拟合。 有人提出来正则化项要足“sparsity、unbiasedness、continuity”,这样Lp没有一个 可以同时满足,所以有人又搞了个SCAD.
Metrics on vector spaces
Norms on vector spaces are equivalent to certain metrics, namely homogeneous, translation-invariant ones. In other words, every norm determines a metric, and some metrics determine a norm.
Given a normed vector space  we can define a metric on X by
we can define a metric on X by
-
 .
.
The metric d is said to be induced by the norm  .
.
Conversely if a metric d on a vector space X satisfies the properties
 (translation invariance)
(translation invariance)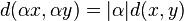 (homogeneity)
(homogeneity)
then we can define a norm on X by
Similarly, a seminorm induces a pseudometric (see below), and a homogeneous, translation invariant pseudometric induces a seminorm.








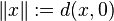














 3231
3231











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








