西瓜书《机器学习》全网最详细解读第一章：绪论

本文链接：https://blog.csdn.net/sherlockMa/article/details/146963656

前言

《机器学习》，又称西瓜书，是南京大学教授周志华教授编著的一本机器学习领域的经典教材。《机器学习》系统地介绍了机器学习的基本理论、常用算法及其应用。全书内容丰富，涵盖了机器学习的多个重要方面，包括监督学习、无监督学习、强化学习等主要学习范式。《机器学习》适合计算机科学、人工智能、数据科学等相关专业的本科生、研究生以及对机器学习感兴趣的自学者。无论是初学者希望系统地学习机器学习的基础知识，还是有一定基础的研究人员和从业者希望深入了解前沿技术，这本书都能提供有价值的参考。

在接下来的日子里，我将每周精心打磨一章内容，全方位、多角度地为大家剖析书中精髓。无论是复杂难懂的算法，还是晦涩难解的公式，我都会以通俗易懂的方式逐一解读，力求让每一位读者都能轻松掌握其中的奥秘。让我们一起在知识的海洋中遨游，探索机器学习的无限魅力！

在本系列中：

重点内容将使用加粗或者红字显示
普通内容使用普通颜色显示
示例使用蓝色显示

1.1 引言

机器学习是一门通过计算手段利用数据（经验）来改善系统性能的学科，其核心是研究从数据中生成模型的学习算法。学习算法基于经验数据产生模型，模型可用于对新情况进行判断。机器学习可视为计算机科学中专注于“学习算法”的分支。

简单来说，机器学习的核心在于通过算法从大量的数据中挖掘出有价值的信息和规律，并将这些规律应用于新的数据，从而实现对未知情况的预测、分类、识别或其他智能决策。它不仅能够处理复杂的模式识别任务，还能在数据不断变化的环境中自我优化和适应，是推动现代人工智能技术发展的核心驱动力之一。

我们举个例子，假设我们有一批西瓜，每颗西瓜都有颜色、纹理、敲击声音等特征，同时我们也知道这些西瓜是好瓜还是坏瓜。学习算法会利用这些特征和结果作为经验数据，从中学习规律，生成一个模型。当遇到一颗新的、尚未剖开的西瓜时，模型会根据其颜色、纹理、敲击声音等特征，判断它是否为好瓜。类似地，在天气预报中，我们有大量的历史气象数据，包括气温、湿度、气压、风速等特征，以及对应的天气结果（如晴天、雨天、阴天等）。学习算法基于这些历史数据生成模型。当输入新的气象数据时，模型就能根据之前学到的规律，预测出当天的天气情况。这种基于经验数据生成模型并用于新情况判断的过程，正是机器学习的核心所在。

1.2 基本术语

机器学习的基石是数据，尤其是海量的数据。通过对大量数据的分析与挖掘，提取其中的内在规律和模式，从而构建出能够进行预测或决策的模型。

以下是机器学习中关于训练的总结：

数据集（Data Set）：数据的集合，是机器学习的基础。我们一般用 $D$ 表示，其包含 m 个示例的数据集，表示为 $D=\left \{ x_1,x_2,...,x_m \right \}$ 。
示例（Instance）/样本（Sample）：每条数据描述了一个对象的信息，称为示例或样本，通常用 x 表示，每个示例由 $d$ 个属性描述，称为维度。每个示例 $x_i$ 是 d 维样本空间 X 中的一个向量，表示为 $x_i=(x_{i1};x_{i2};...;x_{id})$ ，其中 $x_{ij}$ 是 $x_i$ 在第 j 个属性上的取值。
属性（Attribute）/特征（Feature）：数据中描述样本在某些方面的性质，称为属性或特征。
属性值（Attribute Value）：属性的具体取值。
属性空间（Attribute Space）/样本空间（Sample Space）/输入空间（Input Space）：对于一个样本，如果有 n 种属性，则这些属性构成一个 n 维空间，称为样本空间、属性空间或输入空间。
特征向量（Feature Vector）：特征向量是示例的另一种称呼，表示样本在各个属性上的取值集合。

以下是机器学习中关于训练的总结：

学习（Learning）/训练（Training）：从数据集中提取规律并构建模型的过程。
训练数据（Training Data）：用于学习和构建模型的数据。
训练样本（Training Sample）：训练数据中的每一条样本。
训练集（Training Set）：数据集中用于训练模型的部分。
假设（Hypothesis）：通过学习得到的模型，反映了数据集中某种潜在的规律。
真相/真实（Ground-Truth）：数据集本身所蕴含的真实规律。学习过程的目标是使假设尽可能逼近真相。
学习器（Learner）：构建出的模型的别称。

我们的目标是通过训练数据训练一个模型（即假设），使得该假设和真相（真实规律）的差距尽可能小。

以下是机器学习中关于标记的总结：

标记（Label）：与示例结果相关的信息，通常用 y 表示。
样例（Example）：带有标记信息的示例，即同时包含输入特征和输出结果的数据。
标记空间（Label Space）/输出空间（Output Space）：所有可能标记值的集合构成的空间。

假设我们有一个西瓜摊，摊主收集了一批西瓜，并记录了它们的一些特征，比如颜色、纹理、敲击声音等，同时还标记了每个西瓜是否成熟（好瓜或坏瓜）。这些西瓜的数据集合就构成了一个数据集。每个西瓜的数据就是一个示例或样本，它包含了西瓜的各种特征，比如一个西瓜的颜色是“青绿”，纹理是“清晰”，敲击声音是“清脆”，这些特征就是属性，而“青绿”“清晰”“清脆”就是对应的属性值。这些属性值组合在一起，形成了一个西瓜的特征描述。

摊主从这批西瓜中选取一部分数据来训练模型，这部分数据就称为训练数据。通过分析训练数据中的特征和标记（好瓜或坏瓜），学习算法会尝试找出其中的规律，构建一个能够预测西瓜成熟情况的模型，这个模型就是假设。假设的目标是尽可能接近数据集中真实的规律，也就是真相。真相可能是某种隐藏的模式，比如“颜色为青绿且纹理清晰且敲击声音清脆的西瓜通常是好瓜”。学习过程就是让假设不断逼近这个真相。

而每个西瓜是否成熟（好瓜或坏瓜）的信息，就是标记，它是关于示例结果的描述。标记是学习过程中非常重要的部分，因为它告诉学习算法每个样本的正确答案。通过标记，学习算法可以评估假设的好坏，并不断调整，以提高预测的准确性。

以下是机器学习中关于分类和回归任务的总结：

分类（Classification） 是一种典型的学习任务，目的是根据数据的特征将数据集划分为若干个类别。例如，根据西瓜的颜色、纹理和敲击声音等特征，将西瓜分为“好瓜”和“坏瓜”。
- 二分类（Binary Classification） 是一种特殊的分类任务，将数据集分为两类。例如，判断西瓜是否成熟（好瓜或坏瓜）。
  - 正类（Positive Class） 是二分类任务中的一类数据。例如，在判断西瓜是否成熟的问题中，“好瓜”可以被定义为正类。
  - 反类（Negative Class） 是二分类任务中的另一类数据。例如，在判断西瓜是否成熟的问题中，“坏瓜”可以被定义为反类。
- 多分类（Multi-class Classification） 是一种更复杂的分类任务，将数据集分为多个类别。例如，根据西瓜的品种将西瓜分为“黑美人”“麒麟瓜”“无籽瓜”等多个类别。
回归（Regression） 是另一种典型的学习任务，目标是预测数据集对应的结果值。例如，预测西瓜的甜度（一个连续的数值）。

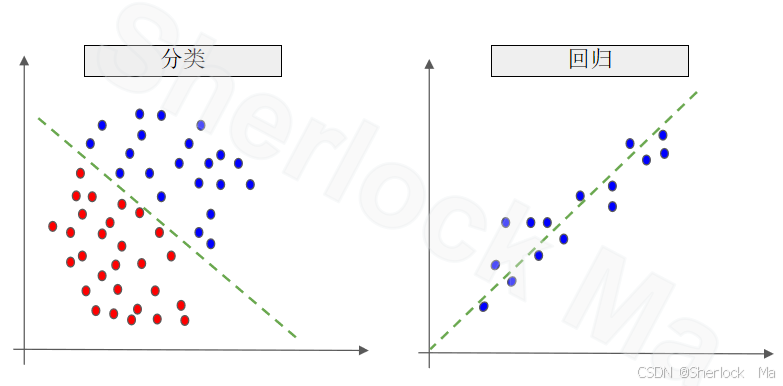
这张图展示了机器学习中的两个基本任务：分类和回归。

左侧的图示代表分类任务。图中有两类数据点，分别用红色和蓝色表示。分类的目标是找到一个决策边界（图中的虚线），将这两类数据点分开。这个决策边界可以是一个直线，也可以是更复杂的形状，取决于所使用的分类算法。分类任务通常用于预测离散的标签，例如判断一封邮件是否为垃圾邮件，或者识别图像中的物体类别。

右侧的图示代表回归任务。图中的数据点同样用不同颜色表示，但这次的目标不是将它们分开，而是找到一个函数（图中的虚线），这个函数能够最好地拟合这些数据点。回归任务通常用于预测连续的数值，例如预测房价、温度或者股票价格等。

总的来说，这张图直观地展示了分类和回归这两种机器学习任务的区别：分类关注的是找到不同类别之间的分界线，而回归关注的是找到一个能够最好地描述数据分布的函数。

以下是关于机器学习中测试相关概念的总结：

测试（Testing）：在机器学习中，测试是指使用学得的模型对新的、未见过的数据进行预测的过程。它是评估模型性能的重要环节。机器学习是一个迭代的过程，通常需要多次进行学习、测试和调整。通过不断地优化模型，最终才能得到准确率最高的模型。
测试样本（Testing Sample）：测试样本是指在测试阶段被模型用来进行预测的样本。这些样本通常是模型在训练过程中未曾见过的，用于评估模型对新数据的泛化能力。

以下是对监督学习和无监督学习的总结：

监督学习（Supervised Learning） 是一种学习方式，其中训练数据包含标记信息。也就是说，每个训练样本不仅有输入特征，还附带了正确的输出结果（标签）。学习算法通过分析这些带有标签的训练数据，学习输入特征与输出结果之间的映射关系，从而构建出能够对新数据进行预测的模型。例如，判断西瓜是否成熟（好瓜或坏瓜）的任务就是典型的监督学习问题，因为每个训练样本都有一个明确的标记（好瓜或坏瓜）。
无监督学习（Unsupervised Learning） 则是另一种学习方式，其中训练数据没有标记信息。在这种情况下，学习算法需要在没有明确指导的情况下，自行发现数据中的结构和模式。聚类就是无监督学习的一个典型例子，因为在聚类任务中，我们不知道每个数据点应该属于哪个类别，算法需要通过分析数据的相似性来自动划分簇。
- 聚类（Clustering） 是一种无监督学习方法，其目标是将训练集中的数据划分为若干个组（簇），这些组在聚类之前是未知的。换句话说，聚类算法会根据数据的内在结构和相似性，自动将数据分为不同的类别，然后再由人类标记具体类别，而不需要事先知道每个数据点的类别标签。

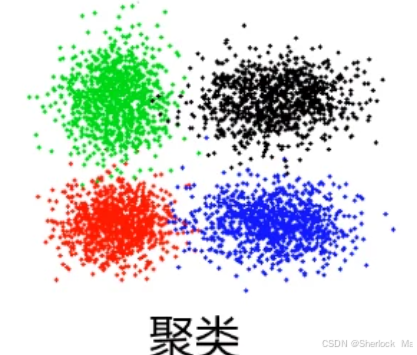
这张图展示了一个聚类分析的结果，图中有四个不同颜色的点群，分别用绿色、黑色、红色和蓝色表示。这些点群代表数据集中被算法识别并分组的四个不同的簇。每个簇中的点在特征空间中彼此接近，表明它们在所考虑的特征上具有相似性。聚类是一种无监督学习方法，其目的是将数据集中的对象分组，使得同一组内的对象之间的相似度高，而不同组之间的对象相似度低。图中的每个点代表一个数据样本，而不同颜色的簇显示了算法如何根据样本的特征将它们划分为不同的组。

以下是机器学习中关于泛化和独立同分布的总结：

泛化（Generalization）：指学得模型适用于新样本的能力。具有良好泛化能力的模型，不仅在训练数据上表现良好，还能在未见过的新数据上做出准确的预测或分类。它反映了模型对整个样本空间的适应性，而不仅仅是对训练集的拟合程度。
独立同分布（Independent and Identically Distributed，i.i.d.）：假设样本空间中的样本是从一个未知的分布 D 中独立地采样得到的，并且每个样本的采样过程是相同的。这意味着每个样本之间相互独立，且它们的概率分布相同。这一假设是机器学习中常用的理论基础，它确保了训练集能够较好地反映样本空间的整体特性，从而为模型的泛化能力提供了理论支持。

1.3 假设空间

归纳(induction)与演绎(deduction)是科学推理的两大基本手段。前者是从特殊到一般的“泛化”(generalization)过程，即从具体的事实总结出一般性规律；后者则是从一般到特殊的“特化”(specialization)过程，即从基础原理推演出具体状况。

假设我们观察了以下具体的西瓜样本：

一个颜色为“青绿”、纹理“清晰”、敲击声音“清脆”的西瓜，它是好瓜。
一个颜色为“浅白”、纹理“模糊”、敲击声音“沉闷”的西瓜，它是坏瓜。
一个颜色为“青绿”、纹理“清晰”、敲击声音“清脆”的西瓜，它是好瓜。
一个颜色为“黑”、纹理“稍糊”、敲击声音“清脆”的西瓜，它是好瓜。

通过这些具体的样本，我们总结出一个一般性的规律：如果一个西瓜的颜色是“青绿”或“黑”，纹理是“清晰”或“稍糊”，敲击声音是“清脆”，那么它很可能是好瓜。这个从具体样本总结出一般性规律的过程就是归纳。

假设我们已经通过归纳得到了一个一般性的规律（假设）：如果一个西瓜的颜色是“青绿”或“黑”，纹理是“清晰”或“稍糊”，敲击声音是“清脆”，那么它很可能是好瓜。

现在，我们遇到了一个具体的西瓜，它的颜色是“青绿”，纹理是“清晰”，敲击声音是“清脆”。根据我们之前总结的一般性规律，我们可以推断这个西瓜很可能是好瓜。这个从一般性规律推导出具体结论的过程就是演绎。

假设空间是指学习算法所考虑的所有可能的假设（或模型）的集合。

假设空间的大小可以是有限的，也可以是无限的。例如：

有限假设空间：如果学习算法只考虑有限个假设，如决策树中只有特定的几种划分方式，或者线性分类器中只考虑有限的权重组合。
无限假设空间：如果学习算法考虑的假设数量是无限的，如线性回归中权重参数可以取任意实数值，或者神经网络中隐藏层节点数量和连接权重可以有无限多种组合。

这个图展示了一个关于西瓜问题的假设空间，它是一个决策树的可视化表示。图中的每个节点代表一个属性的取值，而每个分支则代表属性的不同可能取值。从根节点到叶子节点的路径代表了一个具体的假设，即对西瓜是否为好瓜的判断规则。例如，从根节点到第一个叶子节点的路径表示的假设是：如果一个西瓜的色泽是青绿，根蒂是蜷缩，敲声是浊响，那么这个瓜是好瓜。

图中展示了多个这样的路径，每个路径都对应一个不同的假设。若“色泽”“根蒂”“敲声”分别有 3、2、2 种可能取值，则我们面临的假设空间规模大小为 4 × 3 × 3 + 1 = 37。这是由色泽、根蒂和敲声三个属性的不同取值组合数决定的。

假设空间的选择对学习算法的性能有重要影响：

假设空间过大：可能导致过拟合，即学习算法在训练数据上表现很好，但在未见过的测试数据上表现不佳。这是因为假设空间过于复杂，学习算法可能会捕捉到训练数据中的噪声。
假设空间过小：可能导致欠拟合，即学习算法无法捕捉到数据中的真实规律，导致在训练数据和测试数据上表现都不好。

需注意的是，现实问题中我们常面临很大的假设空间，但学习过程是基于有限样本训练集进行的，因此，可能有多个假设与训练集一致，即存在着一个与训练集一致的“假设集合”，我们称之为“版本空间”(version space)。

假设我们有一个西瓜的训练集，包含以下样本：

色泽 = 青绿，根蒂 = 蜷缩，敲声 = 浊响，标记 = 好瓜
色泽 = 乌黑，根蒂 = 硬挺，敲声 = 清脆，标记 = 坏瓜
色泽 = 浅白，根蒂 = 蜷缩，敲声 = 浊响，标记 = 坏瓜

在这个训练集上，可能存在多个与训练集一致的假设。例如：

假设1：如果色泽是青绿且根蒂是蜷缩，则为好瓜；其他为坏瓜。
假设2：如果色泽是乌黑且根蒂是硬挺，则为坏瓜；其他为好瓜。
假设3：如果色泽是浅白，则为坏瓜；其他为好瓜。

这些假设都能完美地解释训练集中的数据，因此它们都位于版本空间内。版本空间包括了所有这些假设，表示在给定的训练集下，这些都是可能的正确假设。随着更多的数据被加入训练集，版本空间可能会缩小，因为一些假设可能不再与新的数据一致，从而被排除在外。最终，我们希望通过增加更多的数据和调整假设，能够缩小版本空间，找到一个最能泛化到新数据的假设。

1.4 归纳偏好

归纳偏好（Inductive Bias）是指在机器学习中，算法倾向于某些特定类型的假设或模型。这通常是因为算法在设计时就内置了某些先验知识或假设，使得它在学习过程中更倾向于选择符合这些假设的模型。它反映了算法在假设空间中选择特定假设的倾向，可以看作是学习算法自身的一种“价值观”或启发式规则。

归纳偏好在机器学习中是非常重要的，因为它可以帮助我们在巨大的假设空间中进行搜索，找到更有可能正确的模型。然而，归纳偏好的选择也会影响模型的泛化能力，因此需要根据具体问题和数据的特点来合理选择。

任何一个有效的机器学习算法必有其归纳偏好，否则它将被假设空间中看似在训练集上“等效”的假设所迷惑，而无法产生确定的学习结果。可以想象，如果没有偏好，我们的西瓜学习算法产生的模型每次在进行预测时随机抽选训练集上的等效假设。

假设我们继续使用西瓜的例子，我们想要构建一个模型来判断西瓜是否为好瓜。我们有三个属性：色泽（青绿、乌黑、浅白）、根蒂（蜷缩、硬挺）和敲声（浊响、清脆）。我们收集了一些西瓜的数据，并用这些数据来训练我们的模型。

在这个过程中，我们可能会有以下几种归纳偏好：

简单性偏好：我们可能倾向于选择更简单的模型，比如一个只考虑色泽的模型，而不是一个同时考虑色泽、根蒂和敲声的复杂模型。这是因为简单的模型更容易理解和解释，也更不容易过拟合。
平滑性偏好：我们可能倾向于选择一个平滑的模型，即假设西瓜的属性与其是否为好瓜之间的关系是连续的，而不是突变的。例如，我们可能假设色泽从浅白到青绿再到乌黑，西瓜的品质是逐渐变化的，而不是突然变化的。
一致性偏好：我们可能倾向于选择一个与我们先前经验一致的模型。例如，如果我们知道通常青绿的西瓜是好瓜，那么我们可能会倾向于选择一个将青绿色泽作为好瓜重要特征的模型。
可扩展性偏好：我们可能倾向于选择一个可以容易扩展的模型，即如果未来我们想要考虑更多的属性（如重量、形状等），这个模型可以容易地进行扩展。

归纳偏好的重要性

归纳偏好在机器学习中极为重要，它决定了学习算法如何在庞大的假设空间中进行有效的搜索，指导算法倾向于选择某些类型的模型，从而避免过拟合并提高模型的泛化能力。简单模型因其易于理解和解释的特点，通常更受归纳偏好的青睐，这有助于增强模型的可解释性并使决策过程对用户更加透明。归纳偏好还与奥卡姆剃刀原则紧密相关，该原则鼓励在解释力相同的情况下选择最简单的模型。在数据有限的情况下，归纳偏好尤为重要，它帮助算法在信息不足时做出合理的假设。此外，归纳偏好也深刻影响着学习算法的设计，不同的算法可能内置了不同的归纳偏好，这决定了它们在特定类型问题上的表现。总之，归纳偏好是连接数据与模型、算法设计与实际应用之间的桥梁，对于提高学习算法的性能和可靠性起着至关重要的作用。

如何理解任何一个有效的机器学习算法必有其归纳偏好？

这句话强调了归纳偏好在机器学习算法中的必要性。如果没有归纳偏好，算法将无法在众多可能的模型中做出选择，因为从表面上看，这些模型在训练数据上的表现似乎是等效的。以西瓜问题为例，假设我们有多个模型都能完美地解释训练集中的数据，那么如果没有某种偏好来指导选择，算法可能会在每次进行预测时随机选择这些等效模型中的一个，导致预测结果不稳定且不可预测。

归纳偏好的作用是为算法提供一个决策标准，帮助它在众多等效的模型中选择一个或几个更优的模型。这个标准可以是基于模型的简单性、平滑性、一致性或其他任何被认为是重要的特性。通过这种方式，归纳偏好确保了算法能够产生确定且一致的学习结果，而不是在每次预测时随机选择一个模型。

简而言之，归纳偏好是机器学习算法能够从数据中学习并做出一致预测的关键因素。它帮助算法在看似等效的模型中做出选择，从而避免了随机性和不确定性，确保了模型的稳定性和可靠性。

常见的归纳偏好原则有

奥卡姆剃刀原理：在多个与数据一致的假设中，选择最简单的模型
平滑假设：在回归任务中，假设相似的输入应该有相似的输出
局部性假设：例如卷积神经网络（CNN）假设图像中相邻区域的特征相关性较强
平移不变性：CNN假设图像中的目标即使发生平移，其特征仍然保持一致

奥卡姆剃刀

在这里，我们主要介绍奥卡姆剃刀。

奥卡姆剃刀是一种解决问题的原则，它提倡在多个解释或理论中，应选择假设最少、最简单的那个。这个原则源自14世纪英格兰的逻辑学家和方济各会修士威廉·奥卡姆，他提出“不应无必要地增加实体”。在科学和哲学中，奥卡姆剃刀被用来指导理论选择，鼓励人们避免不必要的复杂性，选择最简洁的解释。在机器学习领域，这一原则体现为偏好简单模型，即在解释数据时，如果多个模型具有相同的预测能力，那么应该选择参数最少、结构最简单的模型，因为这样的模型更不容易过拟合，并且更易于理解和维护。简而言之，奥卡姆剃刀鼓励我们在解决问题时追求简洁和高效，避免不必要的复杂性。

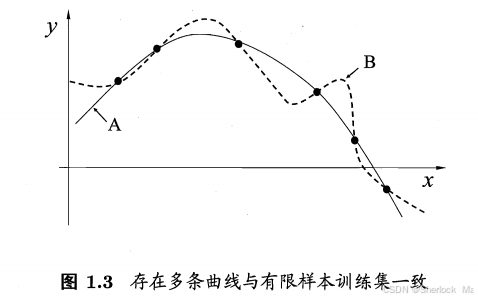
该图展示了一个典型的机器学习场景，其中有多个曲线（A和B）都能够完美地拟合一组有限的训练样本点。这些曲线代表了不同的模型，它们在训练数据上的表现完全相同，但复杂度可能不同。

奥卡姆剃刀原则在这种情况下的应用是建议我们选择最简单的模型。在图中，曲线A相对于曲线B来说可能更简单，因为它的形状更平滑，参数更少，或者更符合我们对数据生成过程的先验知识。尽管曲线B可能在训练集上提供了同样的拟合度，但它的复杂性可能导致在新数据上的泛化能力较差，即更容易过拟合。

因此，根据奥卡姆剃刀原则，我们倾向于选择曲线A作为最终模型，因为它在保持与训练数据一致性的同时，更有可能在未见过的数据上表现良好。这种偏好简单模型的策略有助于提高模型的泛化能力，避免不必要的复杂性，使得模型更加稳健和易于解释。

尽管奥卡姆剃刀原则——即在多个同等解释力的理论中选择假设最少、形式最简单的那个——在理论和实践中被广泛采纳，但该原则的应用并非没有争议，其解释和实施可以有不同的方式。这主要是因为“简单性”这一概念本身是主观的，并且可能根据不同的评价标准而变化。

以西瓜分类问题为例，文中提出了两个分类假设：

假设1：一个西瓜是好瓜当且仅当它的色泽为任意值，根蒂为蜷缩，敲声为浊响。
假设2：一个西瓜是好瓜当且仅当它的色泽为任意值，根蒂为蜷缩，敲声为任意值。

从形式上看，假设1和假设2在逻辑结构上相似，都包含了色泽属性的通配符（表示任意值），根蒂属性的具体值（蜷缩），以及敲声属性的不同处理（假设1中为具体值浊响，假设2中为通配符）。评价这两个假设的简单性并不直观，因为它取决于我们如何定义和衡量“简单性”。

例如，如果我们认为限制更具体的属性值（如假设1中的敲声=浊响）会使模型更复杂，那么假设2看起来更简单。然而，如果我们认为模型中包含更少的条件（如假设2中对敲声没有具体限制）会降低其可解释性，那么假设1可能被视为更简单。

因此，确定哪个假设更简单需要借助其他原则或机制，例如模型的可解释性、泛化能力或与领域知识的一致性等。这表明在实际应用奥卡姆剃刀原则时，我们需要综合考虑多个因素，而不能仅仅依赖于假设的表面形式。

没有免费的午餐定理

让我们再回头看看图 1.3。假设学习算法 $L_a$ 基于某种归纳偏好产生了对应于曲线A的模型，学习算法 $L_b$ 基于另一种归纳偏好产生了对应于曲线B的模型。基于前面讨论的奥卡姆剃刀，我们满怀信心地期待算法 $L_a$ 比 $L_b$ 更好，因为它更简单。

接着，我们把测试样本拿出来，验证两个算法谁好谁坏，图1.4中的黑点代表训练样本，白点代表测试样本。

确实，在图1.4(a)中，曲线A在测试集上的表现优于曲线B，说明在这种情况下，尽管两条曲线都能完美地拟合训练数据，但曲线A具有更好的泛化能力，能够更好地预测未见过的数据。
而在图1.4(b)中，情况则相反，曲线B在测试集上的表现优于曲线A，表明曲线B具有更好的泛化能力。

以上这两种可能性完全都可能存在。

这两幅图共同说明了“没有免费的午餐”定理，即没有任何一个模型能够在所有问题上都表现最好。模型的选择取决于具体的数据分布和任务目标。同时，这也强调了评估模型时需要使用独立的测试集来衡量其泛化能力，而不仅仅是看它在训练集上的表现。通过比较不同模型在测试集上的表现，我们可以更可靠地选择出最优的模型。

我们接下来通过数学方法对NFL定理进行证明：

这个公式描述了机器学习中训练集外误差的数学期望，也就是算法在未知数据上的平均误差。

公式的左边 $E_{ote}(La|X,f)$ 表示在给定数据集 X 和真实规律 f 的情况下，算法 La 的训练集外误差的数学期望。

公式的右边：

$\sum_{x\in \mathbb{X}-X}$ ：X表示训练集整体， $\mathbb{X}$ 表示数据集整体， $\mathbb{X}-X$ 表示训练集外数据（即测试集），x即取出所有测试集数据进行计算。
P(x)：表示这种属性的样本出现的概率。如一个袋子里有红绿蓝球，摸到红球的概率为40%，摸到绿球的概率为30%，摸到蓝球的概率为30%，对其求和
$\mathbb{I}(h(x)\neq f(x))$ 是指示函数，当模型预测值 h(x) 与真实值 f(x) 不相等时，其值为1，否则为0。
$\sum_{h}$ ：h表示模型的所有可能的预测结果，对这些求和。如预测为正例的概率为80%，预测为负例的概率为20%，对其求和
P(h∣X,La) 是在给定训练集 X 和算法 La 的情况下，得到某个模型预测值h的概率， $\sum_{h}$ 表示对所有可能的预测结果进行求和

整个公式的含义是：在给定数据集 X 和真实规律 f 的情况下，算法 La 的训练集外误差的数学期望等于

$\sum_{f}$ ：假设所有可能的规律f以均匀分布出现，这里表示对所有可能的问题的规律进行求和

接下来我们对公式进行推导：

1->2：将式子进行整理，其中仅 $\mathbb{I}(h(x)\neq f(x))$ 包含f，所以移至最后；而P(h∣X,La)包含h，所以移至中间；而所有部分包括x，所以 $\sum_{x\in \mathbb{X}-X}P(x)$ 移至最开始
2->3： $2^{\left | x \right |}$ ，其中 ∣X∣ 是特征空间的维度，即数据集中所有可能性的总数；2表示二分类，对于每一条数据只有两个结果； $\frac{1}{2}$ 表示对于每个数据，有一半的概率满足 $h(x)\neq f(x)$
3->4：将式子进行整理
4->5： $\sum_{h}P(h|X,L_a)$ 加起来是1（因为所有可能的假设是全集，加起来必定是1）

这个公式的推导展示了在某些假设下，算法 La 的训练集外误差的数学期望如何被计算，最终，推导结果显示训练集外误差的期望是一个常数，与算法 La 无关。这意味着在这些假设下，无论使用哪种算法，算法在未知数据上的平均误差期望是相同的。

NFL定理（No Free Lunch Theorem，没有免费午餐定理）。该定理的核心思想是：在所有可能的问题上，没有任何一种算法可以在所有情况下都比其他算法表现得更好。

其隐含意思如下：

如果一个算法在某些问题上表现更好，那么在其他问题上必然表现更差
因此，不存在一种“万能算法”能够解决所有问题
算法的选择必须依赖于具体问题的特性。针对特定类型的问题，设计或选择适合该问题的算法可以显著提高性能

NFL定理的意义

它提醒我们，在选择算法时，必须考虑算法与问题的匹配度
现实世界中的问题并非均匀分布，因此某些算法在特定问题上可能表现更好
该定理也解释了为什么没有一种算法能够在所有问题上都优于随机猜测

亲爱的朋友们，非常感谢您抽出宝贵的时间阅读我的博客。在这里，我分享了一些自己学习的点滴。如果您在阅读过程中有所收获，或者觉得这些内容引起了您的共鸣，希望能得到您的一次点赞，这对我来说是莫大的鼓励。同时，如果您对我的分享感兴趣，不妨关注一下我的博客，这样就能及时收到我的更新通知，不错过更多有趣的内容。另外，如果这些文章对您有帮助，也可以收藏起来，方便日后查阅。您的支持是我不断前行的动力，再次感谢您的陪伴！