数据分析统计知识—描述性统计

Tenshiyu

已于 2022-04-14 22:49:03 修改

阅读量8.6k

点赞数 1

文章标签：数据分析

于 2022-04-14 22:44:41 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/shigure001/article/details/124160094

版权

整理一下自己所掌握的数据分析中涉及的统计学知识点，参考的文章或链接会放在下面，此篇为描述性统计相关，涵盖的并不全面，后续会慢慢的完善，如有纰漏欢迎指正~

目录

知识点参考来源

一、样本常见属性

1.1 位置的度量

1.1.1 算术平均数

1.1.2 加权平均数

1.1.3 中位数

1.1.4 几何平均数

1.1.6 百分位数

1.2 变异程度的度量

1.2.2 四分位数间距IQR

1.2.4 标准差

1.4 分布形态

1.4.1 正态分布

1.4.2 正偏态分布

1.4.3 负偏态分布

1.5 两变量间关系的度量

1.5.1 协方差

1.5.2 相关系数

二、常见定理

2.1 切比雪夫定理

2.2 经验法则（3σ法则）

2.3 幸存者偏差

2.4 辛普森悖论

2.5 异常值检测

2.5.1 z-分数法

2.5.2 上下限法

三、数据分布

3.1 离散型概率分布

3.1.1 二项分布

3.1.2 伯努利分布

3.1.3 泊松分布

3.1.4 超几何分布

3.2 连续型概率分布

3.2.1 均匀分布

3.2.2 正态分布

3.2.3 指数概率分布

知识点参考来源

1.《商务与经济统计》（原书第13版）
2.《校招面试考点全解析——数据分析师篇》
3.百度

一、样本常见属性

1.1 位置的度量

1.1.1 算术平均数

平均数体现的是对数据集的中心位置的度量，当数据来自某个样本时，平均数用x表示；如果数据是来自总体，则我们用希腊字母μ表示。

算术平均数，即一组数据中所有数据之和再除以数据的个数所得到的值

公式为 $\bar{x}= \frac{\sum x_{i}}{n}$

1.1.2 加权平均数

即将各数值乘以相应的权数，然后加总求和得到总体值，再除以总的单位数。

公式为 $\bar{x}=\frac{\sum \omega _{i}x_{i}}{\sum \omega _{i}}$ ，式中， $\omega _{i}$ 为第i个观测值的权重。

1.1.3 中位数

将所有数据按升序排列后，位于中间的数值即为中位数。

当数据量为奇数时，中位数就是位于中间那个数值；当数据量为偶数时，中位数是中间两个数值的平均数。

当数据集中含有极端值时，使用中位数作为中心位置的度量会比平均数更合适。比如，计算全国人民的收入时，中位数就比平均数更能体现收入的中心位置。

1.1.4 几何平均数

它是n个数值乘积的n次方根，记为 $\bar{x_{g}}$ ，常常用于分析如增长率等问题。

公式为 $\bar{x_{g}}=\sqrt[n]{x_{1}x_{2}x_{3}x_{4}..x_{n}}$

1.1.5 众数

众数即为数据集中出现次数最多的数据。

1.1.6 百分位数

百分位数提供了数据是如何散布在从最小值到最大值的区间上的信息。

第p百分位数位置 $L_{p}=\frac{p}{100}(n+1)$ ，n为数据量。

其中，四分位数是一种特殊的百分位数，它将数据划分为四部分，每一部分大约包含了 $\frac{1}{4}$ 的观测值，因此可以用计算百分位数的方法计算四分位数。

一般： $Q_{1}$ =第一四分位数，又叫第25百分位数

$Q_{2}$ =第二四分位数，又叫第50百分位数，同时也是中位数

$Q_{3}$ =第三四分位数，又叫第75百分位数

1.2 变异程度的度量

除了位置的度量外，我们往往还需要考虑变异程度，即离散程度的度量。

1.2.1 极差

是最容易计算的体现变异程度的度量，同时也极易受到异常值的影响。

极差=最大值-最小值

1.2.2 四分位数间距IQR

为第三四分位数 $Q_{3}$ -第一四分位数 $Q_{1}$ 的差值，即为中间50%的极差。

1.2.3 方差

是最常见的变异程度的度量，依赖于每个观察值（ $x_{i}$ ）与平均值之间的差异。

总体方差 $\sigma ^{2}=\frac{\sum \left ( x_{i}-\mu \right )}{N}^{2}$ ，μ为总体均值，N为总体的数据量

样本方差 $s^{2}=\frac{\sum (x_{i}-\bar{x})}{n-1}$ ， $\bar{x}$ 为样本均值，n为样本的数据量

1.2.4 标准差

标准差为方差的正平方根。

样本标准差 $s=\sqrt{s^{2}}$

总体标准差 $\sigma =\sqrt{\sigma ^{2}}$

1.3 Z-分数

z-分数作为相对位置的度量值，可以帮助我们确定一个数据离平均数有多远。

z-分数也称为标准化数值。

$z_{i}=\frac{x_{i}-\bar{x}}{s}$

1.4 分布形态

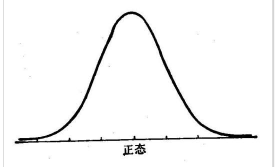
1.4.1 正态分布

变量的频数或者频率呈现中间最多，两端逐渐对称减少的一种分布规律。

举例：一个年级学生的身高分布呈一个正态分布。

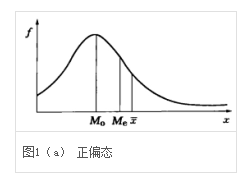
1.4.2 正偏态分布

又叫做右偏态分布，特征是其平均数大于中位数，中数又大于众数，这样的一组数据的分布是属于正偏态分布。

1.4.3 负偏态分布

又叫做左偏态分布，特征是其平均数小于中位数，中数又小于于众数，则数据的分布是属于负偏态分布。

1.5 两变量间关系的度量

1.5.1 协方差

样本协方差 $s_{xy}=\frac{\sum (x_{i}-\bar{x})(y_{i}-\bar{y})}{n-1}$

我们将每个 $x_{i}$ 与其样本的平均数 $\bar{x}$ 的离差乘以对应的 $y_{i}$ 与其样本平均数 $\bar{y}$ 的离差，再将所有结果加总，然后除以n-1，所得的结果即为样本协方差。协方差值越大，正线性相关关系越强，值越小，负线性相关关系也就越小。

1.5.2 相关系数

这里我们只涉及皮尔逊相关系数。又称为线性相关系数，仅仅只能判断样本间变量是否存在线性关系，由协方差与方差的比值计算而来，取值在-1到1之间：

$r_{xy}=\frac{s_{xy}}{s_{x}s_{y}}$

相关系数的绝对值越接近于1，线性相关关系越强，越接近于0，线性相关关系越弱。

二、常见定理

2.1 切比雪夫定理

与平均数的距离在z个标准差之内的数据值所占的比例至少为 $(1-\frac{1}{z^{2}})$ ，其中z是大于1的任意实数。

当z=2,3,4时，该定理的一些应用如下：

至少0.75或75%的数据值与平均数的距离在z=2个标准差之内
至少0.89或89%的数据值与平均数的距离在z=3个标准差之内
至少0.94或94%的数据值与平均数的距离在z=4个标准差之内

2.2 经验法则（3σ法则）

对于钟型分布（即正态分布）的数据，有

大约68%的数据值与平均数在1个标准差之内
大约95%的数据值与平均数在2个标准差之内
几乎所有的数据值与平均数在3个标准差之内

2.3 幸存者偏差

只看了经过某种筛选而产生的结果，却没有意识到筛选的过程，因此忽略了被筛选掉的关键信息，在幸存者偏差这个问题中，我们观察到的样本是被筛选过的有偏样本。

2.4 辛普森悖论

指某个条件下两组数据单独分析得到的结论，可能与将其综合起来分析得到的结论截然相反。辛普森悖论在A/B试验中常作为高频考点出现，这时候实验结果值得我们细细斟酌，甚至需要重新分配流量再次测试。

2.5 异常值检测

2.5.1 z-分数法

z-分数可以用来检测异常值，经验法则告诉我们，对于正态分布的数据，几乎所有的数据值与平均数的距离都在3个标准差之内，因此，在利用z-分数法来检测异常值时，可以把z-分数小于-3或者大于+3的所有数值都视作为异常值。

2.5.2 上下限法

确定异常值的另一种方法是上下限法，以第一四分位数 $(Q_{1})$ 与第三四分位数 $(Q_{3})$ 以及四分位数间距IQR为依据。首先我们计算数据集的上限和下限

上限= $Q_{3}+1.5*IQR$
下限= $Q_{1}-1.5*IQR$
IQR= $Q_{3}-Q_{1}$

如果一个观测值的数值大于上限或小于下限，则将其视作为为异常值。

三、数据分布

3.1 离散型概率分布

3.1.1 二项分布

指统计变量中只有性质不同的两项群体的概率分布。

二项代表事件往往只有两种可能的结果，一种是成功，另一种是失败。在n次独立重复的实验中，假设每次实验A事件发生概率为p，X表示A事件发生的次数.

存在公式： $P\left \{ X=k \right \}=\binom{n}{k}p^{k}(1-p)^{n-k}$

性质：

1）由一系列相同的n个试验组成

2）每次试验都有两种可能的结果，我们把其中一个称为成功，另一个称为失败

3）每次试验成功的概率都是相同的，用p来表示，失败的概率也相同，用1-p表示

4）试验是相互独立的

3.1.2 伯努利分布

在概率论和统计学中，二项分布是n个独立的成功/失败试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当n=1时，二项分布就是伯努利分布。

3.1.3 泊松分布

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。在排队论中使用比较广泛，比如说，在一个医院中，假设每个病人来看病的概率都是随机且独立的，那么这个医院在一天内接受的病人呈泊松分布。

泊松分布的概率函数为： $P(X=k)=\frac{\lambda ^{k}}{k!}e^{-\lambda },k=0,1,...$

泊松分布的参数λ是单位时间（或单位面积）内随机事件的平均发生次数。k为预计发生的次数。

3.1.4 超几何分布

超几何分布是统计学上一种离散概率分布。它描述了从有限N个物件（其中包含M个指定种类的物件）中抽出n个物件，成功抽出该指定种类的物件的次数（不放回）。

3.2 连续型概率分布

3.2.1 均匀分布

均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。

假设x服从[a,b]上的均匀分布，则x的概率密度函数如下：

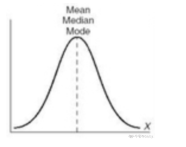
$f(x)=\left\{\begin{matrix} 0,x<a \cup x>b \\ \frac{1}{b-a},a\leqslant x\leq b \end{matrix}\right.$

3.2.2 正态分布

变量的频数或者频率呈现出中间最多，两端逐渐对称减少的一种分布规律。对于正态分布而言，均值=中位数=众数。

3.2.3 指数概率分布

可用于描述如打到某加油站的两辆车时间间隔、高速路上两起重大事故发生地之间的距离等随机变量。

定义：连续随机变量X服从参数为λ的指数分布，其中λ>0为常数，记为X~E(λ)，它的概率密度为

$\left\{\begin{matrix} f(x)=\lambda e^{-\lambda x},x>0\\f(x)=0,x\leq 0 \end{matrix}\right.$

关注

1
点赞
踩
10

收藏

觉得还不错? 一键收藏
0
评论
数据分析统计知识—描述性统计

整理一下自己所掌握的数据分析中涉及的统计知识，参考的文章或链接会放在下面，此篇为描述性统计相关，可能涵盖的并不全面，后续会慢慢的完善，如有纰漏欢迎指正~目录知识点参考来源一、样本常见属性1.1位置的度量1.1.1 算术平均数1.1.2加权平均数1.1.3中位数1.1.4几何平均数1.1.5众数1.1.6百分位数1.2变异程度的度量知识点参考来源1.《商务与经济统计》（原书第13版）2.《校招面试考点全解析——数据分析师篇》3.百度...
复制链接

扫一扫

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。