考研数学一线性代数--常见的重要结论

本文链接：https://blog.csdn.net/shijizhe1/article/details/147218005

记录去年考研期间学习数学一线性代数部分整理的一些重要结论。
线性代数我基础阶段跟的张宇，强化阶段跟的姜晓千。正如张宇老师所说，线性代数是一个章节之间联系十分紧密的学科，当给出一个矩阵时，我们要将其能够灵活的转化到向量组、秩序等不同的角度，才能在做题时更加得心应手，尤其是选择填空题。因此，线性代数记住一些常用的结论是非常有用的。
因为我都是在CSDN写博客，所以就把这篇文章分享在这里吧，也不知道合不合适。如果有幸被看到，希望能帮助到正在准备考试的你😊

一、行列式

宽对角行列式（也称三对角行列式）

具体的推导可以应用差分方程或者递推，可以去B站找推导视频，有很多。
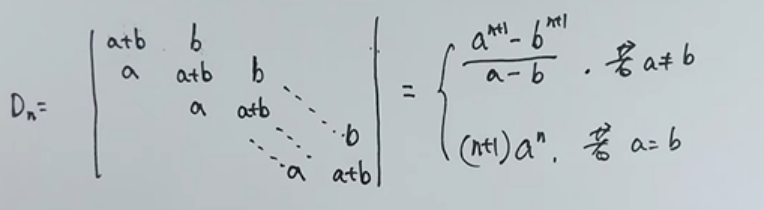
在这里插入图片描述
对于下方这个行列式，只要满足：a分解为两个数相加（即a1+a2=a），且a1*a2= b*c,即可使用上述公式计算。

再看一个例子，这里的2a可以分解为a+a，满足a*a=(a^2 )*1，可以用上述结论。
在这里插入图片描述

二、矩阵

（一）矩阵的迹

对角线元素之和

（二）主子式和顺序主子式

主子式：从相同的行和列号中选取组成的子式

例如：
（1）对于一个七阶方阵，选取行号（如 1、3、7行），再选取相同行号的列号（1、3、7 列）
组成的三阶方阵。
（2）三阶方阵：
一阶主子式：a11 a22 a33
二阶主子式：
在这里插入图片描述
三阶主子式：A33 本身

顺序主子式：在上述的基础上，由该方阵的前k行和k列元素组成。
也就是说，对于一个三阶方阵，最多只能有三个顺序主子式： A11，A22，A33

（三）矩阵的转置T

仅转置独有的可加性：
在这里插入图片描述

（四）矩阵求逆

1）简单矩阵

①主对角、副对角矩阵：主对角直接求逆，副对角倒序求逆。
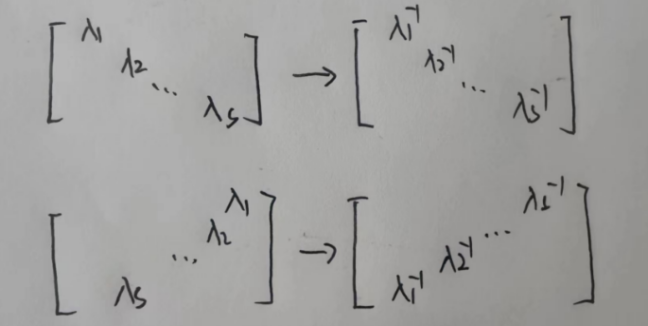
在这里插入图片描述

2）分块矩阵

②主对角、副对角分块矩阵：主对角直接求逆，副对角倒序求逆
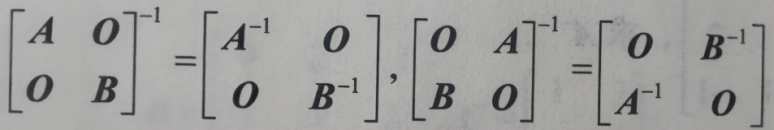
在这里插入图片描述
③三角、反三角分块阵
三角阵：对角线求逆，副对角： 左乘同行，右乘同列，再加负号。
反三角阵：先对调，求副对角逆，然后按照： 左乘同行，右乘同列，再加负号。
有点绕，看图：

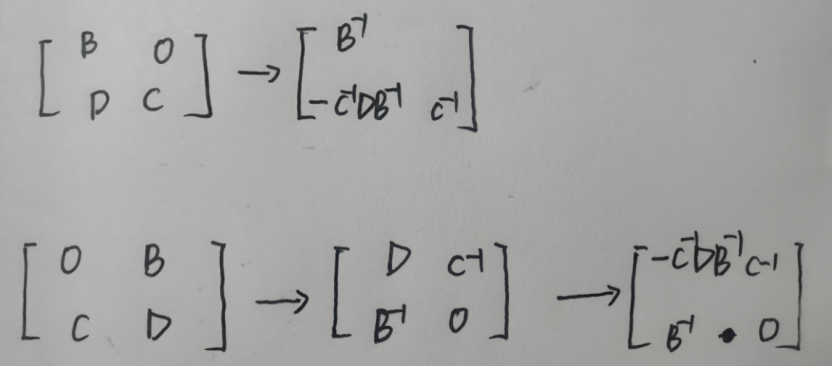
3）利用伴随矩阵

④ 二阶矩阵
二阶矩阵伴随： 主对调，副变号。
利用公式，求出逆。
在这里插入图片描述

4）利用初等变换

[A|E] = [E|A^-1]

（五）矩阵求 n次方

1）简单矩阵

①主对角线矩阵: 对角线上元素分别n次方
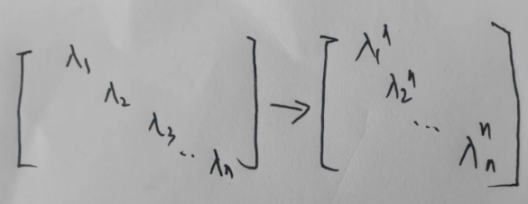
在这里插入图片描述
②主对角线分块矩阵: 对角线上元素分别n次方

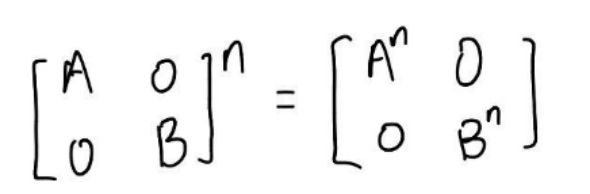
2）秩一矩阵

A_n= tr(A)^n-1 * A

（六）初等矩阵的性质（转置、逆、行列式）

来自：张宇线代基础9讲
在这里插入图片描述

（七）矩阵逆、转置、伴随三者共性

1）作用于矩阵无先后顺序

即可以任意：从括号内外交换位置
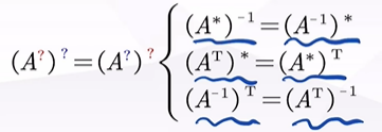
在这里插入图片描述

2）都适用于穿脱原则

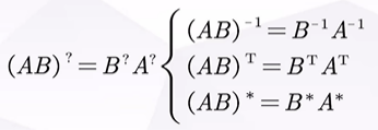
在这里插入图片描述

3）m次幂无先后顺序

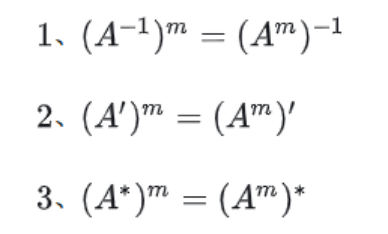
在这里插入图片描述

4）数字k倍（不同点）

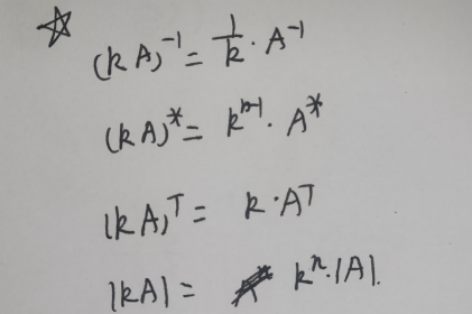
在这里插入图片描述

（八）矩阵的秩（重要⭐️）

1）初等变换不改变矩阵的秩

由于可逆矩阵可以表示成：有限个初等矩阵的乘积
所以：
r(A) = r(PA) = r(AQ) = r(PAQ)

2）左乘列满秩或者右乘行满秩，不改变原来的秩

r(A_nMaxB) = r(B)
r(AB_nMax) = r(A)
可以从多个角度证明：
① 利用公式：
r(AB) >= r(B) + r(A) - n (n为A的列，B的行)
A列满秩，r(A) = n ===> r(AB) >= r(B)
矩阵秩越乘越小， r(AB) <= r(B)
综上r(AB)= r(B)

② 线性方程组： B_nxs X=0 与 A_mxnB_nxs X=0 同解
若BX=0 ===> ABX = 0
若ABX =0，A为列满秩 ==> BX=0 （A为列满秩，则Ax=0，只有零解。AB=0–>B=0）
所以二者同解，秩相同

③由上述结论可以证明下述两个重要结论：
A列满秩，矩阵C(C=AB) 的行向量组与B的行向量组等价。

AB=C，C的行向量可由B的行向量表示，即r(B) = r(B/C)
A列满秩，r(B) = r(C )

综上，单方面表示+秩相等==>三秩相等====>等价

同理，B行满秩，矩阵C(C=AB) 的列向量组与A的列向量组等价。

C列可由A列线性表示
r(A) = r(C )

3） r(A) = r(A^T) = r(AA^T) = r(A^TA)

是用Ax=0和A^TAx=0同解证出来的（证明见下方线性方程组，见后边特殊汇总也行）

4）A可相似对角化，r（A）为非0特征值的个数。

5）几个常见不等式

来自张宇-线性代数
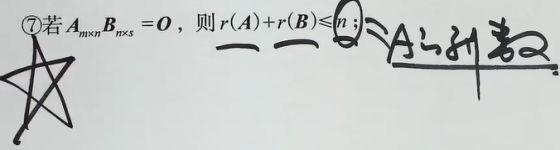
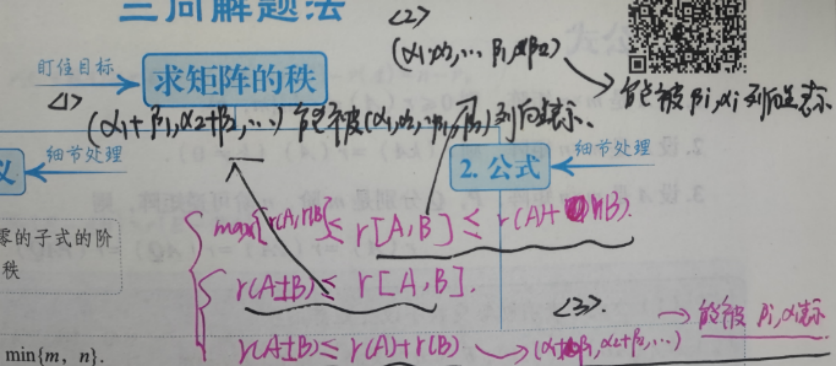
在这里插入图片描述

（九）行阶梯型与等价标准型

任何矩阵都可以使用初等行变换变为 行阶梯型、行最简阶梯型

任何矩阵都可以通过 初等变换（行+列） 变为 等价标准型（Er 0）

任何可逆矩阵都可以通过初等行变换变成单位矩阵（因为可逆矩阵的行最简阶梯型就已经是E了）

三、向量

（一）标准（单位）正交向量组、规范正交基

α1,α2,…,αs 满足:
①两两正交
②模为1

（二）向量组等价

1）定义：向量组 Ⅰ,Ⅱ 可以相互线性表示
2）判断条件：
①三秩相等： r(Ⅰ) = r(Ⅱ) = r(Ⅰ,Ⅱ)
②单方面表示 + r(Ⅰ) = r(Ⅱ)

四、线性方程组

（一）齐次方程解的特性

1）齐次的通解解答格式： k1ζ1 + k2ζ2 + … + kn-rζn-r 其中k1,k2,…kn-r为任意常数
2）若Aζ1=0 Aζ2=0，则 A(k1ζ1 + k2ζ2)=0. 即：齐次方程解的线性组合，仍是方程的解。

（二）非齐次方程解的特性

1）非齐次的通解 = 齐次的通解 + 非齐次的特解
2）η1、η2是非齐次方程的解则: η1-η2 是对应齐次方程的解

（三）公共解求法

参考了某大佬的文章，原博客地址忘记了。

1）联立方程组求解

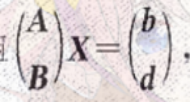
在这里插入图片描述

2）解出（1）的通解后，再带入（2）

3）分别求出（1）（2）的通解，令通解相等，解出公共解

注意最后一步找k，l的关系求法

可以直接相等，得到关系
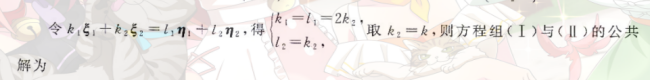
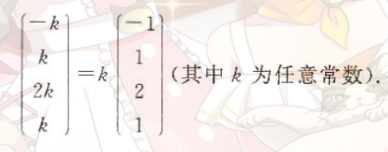
也可以移项组成新的线性方程组，得到关系

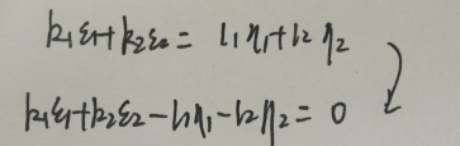
系数矩阵：(a1, a2, -b1, -b2) 初等行变换：

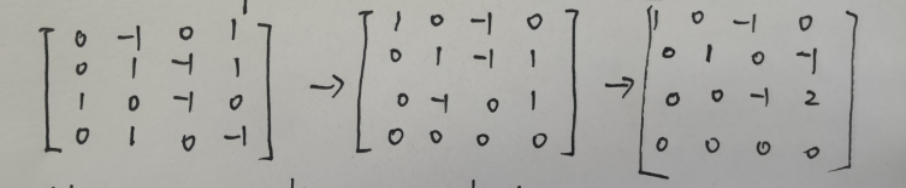
系数矩阵化简后，列出l1,l2,k1,k2 的等式（直接列x1-x2=0的等式），得到他们之间的关系

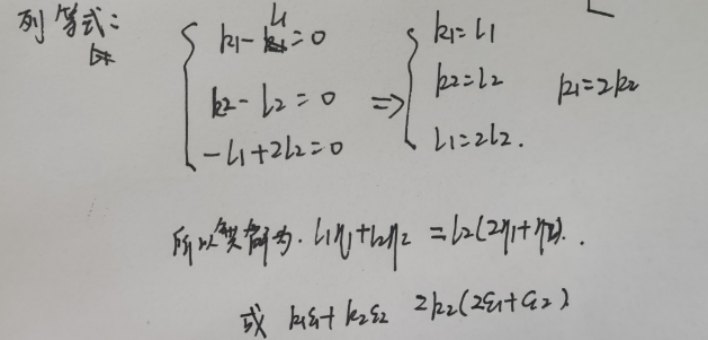
（四）证明四秩相等r(A) = r(AT) = r(AAT) = r(ATA)

1）r(A) = r(AT)
行列式行列等价，转置不影响秩，此项无需证明。
2）r(A) = r(ATA)
使用结论：如果Ax=0与ATAx=0同解，则r(A) = r(ATA)
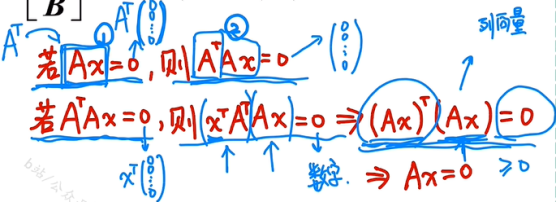
在这里插入图片描述

3）将2)中转置，使A = AT ,得到：r(AT) = r(AAT)

综上，四秩相等成立

五、特征值与特征向量、相似对角化

（一）n阶矩阵相似的两个充要条件

有n个线性无关的特征向量
对应于每个k重特征值都有k个线性无关的特征向量

（二）n阶矩阵相似的两个充分条件（能推出相似）

实对称矩阵 一定可以相似对角化
有n个不同的特征值 一定可以相似对角化

（三）特征值和秩的关系

A可相似对角化，r（A）为非0特征值的个数。

六、二次型、合同

（一）合同注意问题：

对称矩阵和非对称矩阵一定不合同（AB合同，一个为对称矩阵，另一个必为对称矩阵）
二次型f=xTAx以及二次型正定均要求A在实对称矩阵范围内

（二）变换为标准型两种形式：

可逆线性变换x=Cy(矩阵C一定要是可逆的，这个要实际去验证)
正交变换x=Qy

（三）标准型、规范型答题规范：

标准型、规范型都是经过变换得来的，因此问xTAx的标准型、规范型应当回答：
变换后的字母：例如:y₁²+y₂²+y₃²

（四）线性变换答题规范

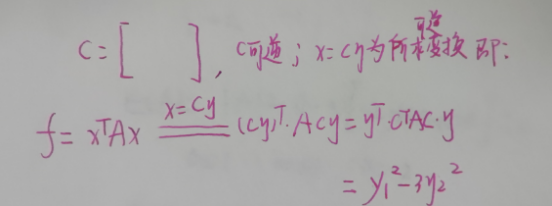
在这里插入图片描述

七、特殊汇总(重要⭐️)

（一）秩1矩阵

1）向量形式：

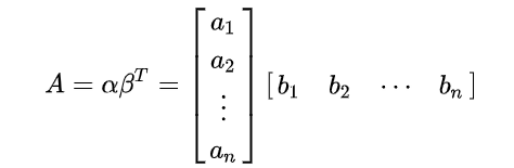
在这里插入图片描述

2）迹：

内积（a₁b₁+a₂b₂+a₃b₃+…+a_nb_n） = 迹
tr（A） = b^Ta = a^Tb （都是数，你乘我，我乘你一样）
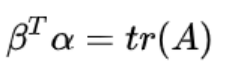
在这里插入图片描述

3）特征值：

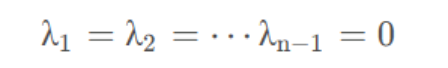
在这里插入图片描述

证明：
因为秩r(A)=1，所有S=n-r(A)=n-1，存在a1，a2，…，an-1（n-1个特征向量）
满足： Aa1 = 0 = 0a1,
所以λ=0，至少是n-1重根，
又因为λ1+λ2+…+λn = 内积
所以至少有一个λ=内积，那剩下的λ至多为n-1重根。
综上，得证。

4）特征向量： A = ab^T

①tr（A）不为0
Aa = ab^Ta = a(b^Ta) (括号里是个数)
所以l1 = b^Ta对应的特征向量为a
l2 = l3 = … = ln = 0,解(A-0E)x = 0; 即ab^T x=0（a为一维列向量，所以列满秩，左乘列满秩不改变方程的解abx=0与bx=0同解）
也就是b^T x=0，可以得到n-1个线性无关的解。
②tr（A）=0
l1 = l2 = l3 = … = ln = 0
解b^T x=0，可以得到n-1个线性无关的解。

5）相似对角化

tr（A）不为0，可以相似对角化

6）n次方

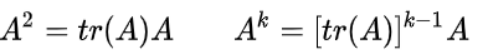
在这里插入图片描述

（二）正交矩阵

1）定义： AA^T= A^TA = E

2）充要条件：

A^T = A ^-1
A的行（列）向量是规范正交基

3）特点：

①行列式只能为：-1或者1，所以正交矩阵一定可逆
②-1，*，T，n次方，AB都为正交矩阵
③实特征值为-1或者1
④如果|A|=-1：则至少有一个特征值为-1
⑤如果|A|=1且n为奇数：则至少有一个特征值为1[如果都为-1，则行列式（-1）²ⁿ⁺¹为-1]

上述证明:
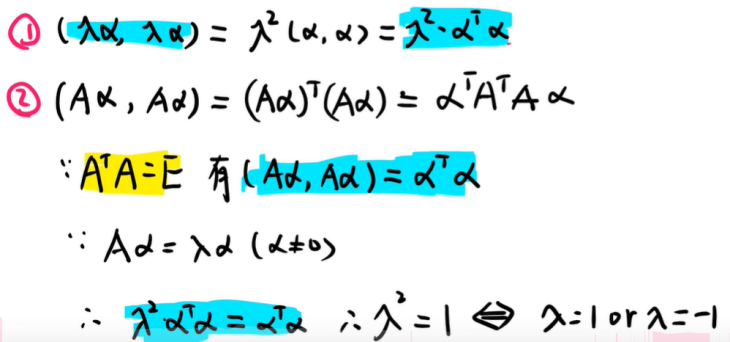
在这里插入图片描述

（三）实对称矩阵

1）定义： A^T = A（转置等于本身）

2）一定可以相似对角化（可以正交相似对角化）

3）特征向量性质

属于不同特征值的特征向量一定正交
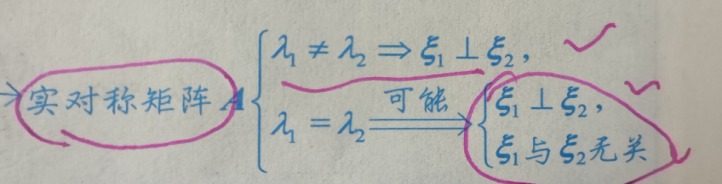
在这里插入图片描述

4）秩等于非零特征值个数

（四）分块矩阵

1）求逆

2）求n次方

3）求行列式

拉普拉斯展开式

4）求秩

对于三角阵： r(A)+r(B)≤r≤r(A)+r(B)+r(C )
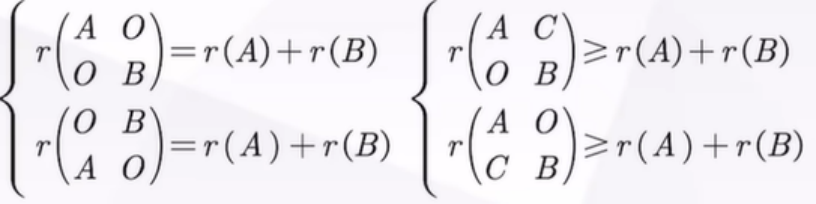
在这里插入图片描述

5）求转置

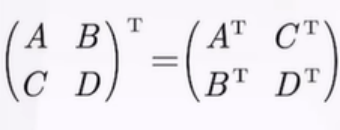
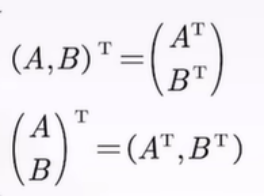
在这里插入图片描述

6）分块矩阵服从广义的初等变换

服从左行右列

（五）若Ax =0的解均是Bx = 0的解五个结论

1）几何意义： B的解把A的所有解①包含在内

A是公共解，联想到方程组联立
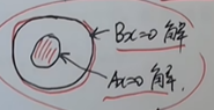
在这里插入图片描述
也就是说，A的约束条件更大，解空间维数更低

2）A，B秩的关系：r(A)≥r(B)

3）Ax =0 和（A/B）x=0 同解（是①的充要条件）

A的都是B的，说明A的解是二者公共的解，可以考虑到线性方程组同解/公共解：联立方程
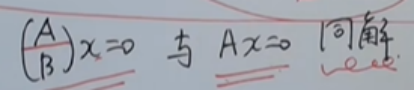
在这里插入图片描述
证明：

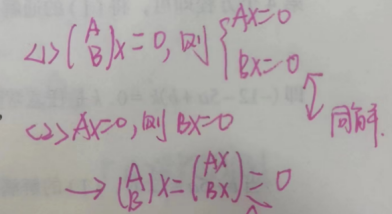
4）A/B和A矩阵秩关系（充要）

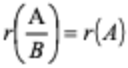
在这里插入图片描述

5）B的行向量组可由A的行向量组线性表示（充要）

这个结论前面也有证明

6）一定存在矩阵P，使得 B = PA（充要）

（六）向量组b1,b2,…bl可由a1,a2,…am线性表示(都是n维)

1）定义：

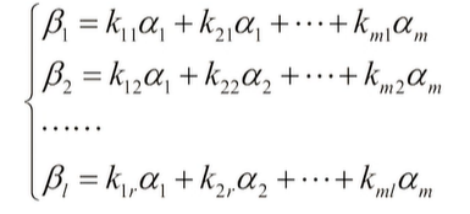
在这里插入图片描述

2）向量组秩：r(B)<=r(A)

高维能表示低维

3）方程组角度：Ax = B有解

4）[A]与]A,B]秩的关系：

秩：系数矩阵=增广矩阵
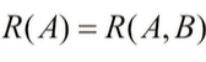
在这里插入图片描述

5）等价矩阵：B = AP

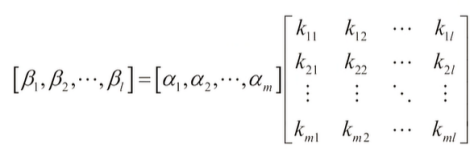
在这里插入图片描述
即存在矩阵P，使得：B = AP

6）矩阵列向量角度：

矩阵B[b1,b2,…bs]的列向量，均可由矩阵A[a1,a2,…am]的列向量线性表示

（七）AB=C <-----> C与A、B线性表示的理解

在这里插入图片描述

1）如何理解秩：

在这里插入图片描述
列向量线性表示：联想向量等价、单方面线性表示
行向量线性表示：联想线性方程组同解、单方向解

2）如何理解线性表示：

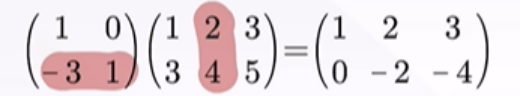
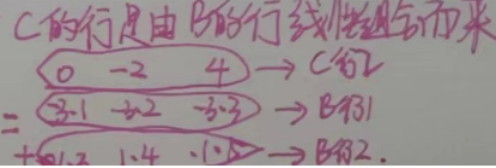
在这里插入图片描述

111

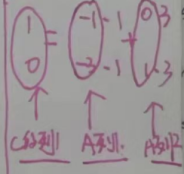
（八）空间中三平面关系转化为线性方程组的解

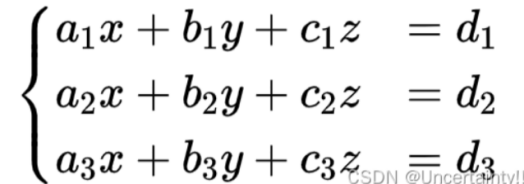
在这里插入图片描述
系数矩阵的一个行向量为其对应平面的法向量，平面相交意味着：
==>平面对应的法向量不成比例(不共线)
==>即系数矩阵行向量线性无关
==>即系数矩阵非零行的情况（系数矩阵秩的情况）

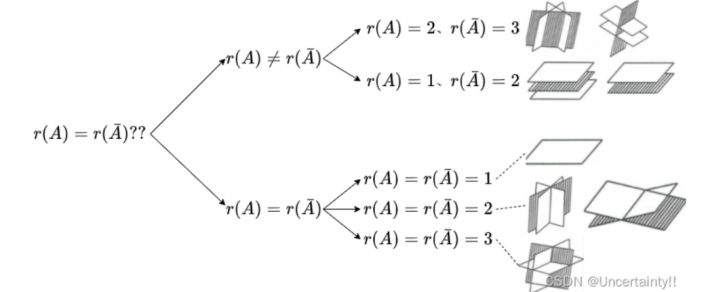
参考文章：用秩讨论线性方程组的解/三个平面的位置关系_平面互异-CSDN博客

（九）解方程组时如何设自由变量

向量线性表示时：（或者非齐次通解时）
直接设自由变量k，解非齐次方程

解线性方程组通解：
自由变量为1：解齐次方程组，得到基础解系
自由变量为0：解非齐次方程组，得到特解

解特征向量：
本质上是基础解系，
自由变量为1：解齐次方程组

（十）基础解系、线性方程组通解、（全部）特征向量答题时区别

在这里插入图片描述

（十一）向量、矩阵考研书写规范

向量：小括号 (1,2,3)
矩阵：也用小括号
在这里插入图片描述

末尾

强烈推荐姜晓千老师的线代强化课
里面总结了很多题型：例如aij=aji能推出什么结论，行满秩、列满秩的矩阵各有什么特性等，我本来是记在张宇基础线代9讲这本上来着，但是这本书被我考完试丢在老家了，因此也不放在这里总结了，觉得有帮助的可以自己去看看。
功不唐捐，玉汝于成，祝大家都能取得理想的成绩。

君子终日乾乾，夕惕若厉，无咎。